自动搬运

查看原文

来自洛谷，原作者为

	Graphcity 循此苦旅，终抵繁星。

搬运于2025-08-24 22:25:27，当前版本为作者最后更新于2023-02-23 21:35:32，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

首先可以通过翻转坐标系（也就是 $x,y$ 取相反数）的方式使得终点满足 $x\ge 0,y\ge 0$。

我们希望尽量让从左上到右下，拐点在左下方的 “L” 形块接通 $(0,0)$ 到 $(x,y)$。不妨令当前点在 $(a,b)$，且必然有 $(x,y)$ 在 L 形块的右下方，分类讨论：

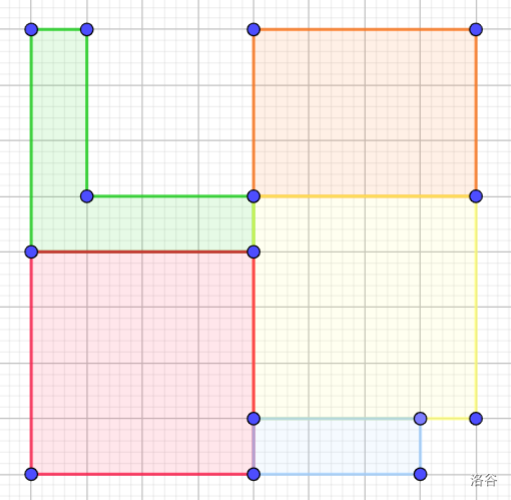
• $(a,b)$ 走一步即可到达 $(x,y)$：

  • $x\in [a,a+n-1]$，$y\in (b,b+n]$（黄色部分）：直接填 $(x-n+1,b+1)$，$(b+1,b+n)$。
  • $x\in[a-n+1,a)$，$y\in (b,b+n]$（橙色部分）：这个时候需要把 L 形块上下翻转，填 $(x+n-1,b+1)$，$(x,b+n)$。
  • $x\in (a,a+n]$，$y\in [b-n+1,b]$（红色部分）：直接填 $(a+1,y)$，$(a+n,y+n-1)$。
  • $x\in (a,a+n]$，$y\in (b,b+n-1]$（蓝色部分）：直接填 $(a+1,b)$，$a+n,b+n-1$。

• 如果还走不到：

  • $x\in (a-n,a]$，直接往下平移。
  • $y\in (b-n,b]$：直接往右平移。
  • $x-a\ge y-b$：往右下角平移，左上角端点在 $(a+1,b)$。
  • $x-a<y-b$：往右下角平移，左上角端点在 $(a,b+1)$。

对于这题，有一点特别注意的：固定两个端点会得到两个不同的 L 形块，所以本题区分 L 形块的依据之一就是端点的顺序。一定要写对端点的顺序。

#include<bits/stdc++.h>
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rof(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
const int Maxn=2e5;

int T,n,a,b,opx,opy;
vector<array<int,4>> ans;

inline void Solve()
{
    cin>>a>>b>>n; opx=1,opy=1;
    if(a<0) a=-a,opx*=-1;
    if(b<0) b=-b,opy*=-1;
    if(a==0 && b==0) {printf("0\n"); return;}
    int x=a,y=b; a=0,b=-1;
    while(1)
    {
        if(y>b && x>=a && x<=a+n-1 && y<=b+n)
        {
            ans.push_back({x-n+1,b+1,x,b+n});
            break;
        }
        if(y>b && y<=b+n && x<a)
        {
            ans.push_back({x+n-1,b+1,x,b+n});
            break;
        }
        if(b>=0 && x>a && x<=a+n && y<=b)
        {
            ans.push_back({a+1,y,a+n,y+n-1});
            break;
        }
        if(b>=0 && x>a && x<=a+n && y<=b+n-1)
        {
            ans.push_back({a+1,b,a+n,b+n-1});
            break;
        }
        if(x>=a-n+1 && x<=a)
        {
            ans.push_back({a-n+1,b+1,a,b+n}),b+=n;
            continue;
        }
        if(b>=0 && y>=b-n+1 && y<=b)
        {
            ans.push_back({a+1,b-n+1,a+n,b}),a+=n;
            continue;
        }
        if(b>=0 && x-a>y-b)
        {
            ans.push_back({a+1,b,a+n,b+n-1}),a+=n,b+=n-1;
            continue;
        }
        ans.push_back({a,b+1,a+n-1,b+n}),a+=n-1,b+=n;
        continue;
    }
    cout<<ans.size()<<endl;
    for(auto i:ans)
    {
        int a=i[0]*opx,b=i[1]*opy,c=i[2]*opx,d=i[3]*opy;
        swap(a,c),swap(b,d);
        printf("%d %d %d %d\n",a,b,c,d);
    }
    ans.clear();
}

int main()
{
    cin>>T;
    while(T--) Solve();
    return 0;
}