自动搬运

查看原文

来自洛谷，原作者为

	0000pnc 几人仍眼睛明亮 几人已失了魂

搬运于2025-08-24 22:25:13，当前版本为作者最后更新于2024-09-23 21:14:46，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

神仙题。

首先如果所有的 $a_{i}$ 之和为奇数那么一定无解。

然后这里有个关键观察：对于 $n\ge 2$，一个 n-quotation 序列（即由若干个 n-quotation 拼接而成的序列）一定是一个完整的 n-quotation。

证明考虑归纳。首先对于 $n=2$ 是比较容易的，把首尾的两个引号分别去掉后剩下的一定是一个 1-quotation 序列（因为所有数之和是偶数，一定能够找到合适的匹配）。

如果 $n=k-1$ 时成立，那么 $n=k$ 时每个 n-quotation 都会恰好包括一个 (n-1)-quotation。此时这个序列大概长这样：

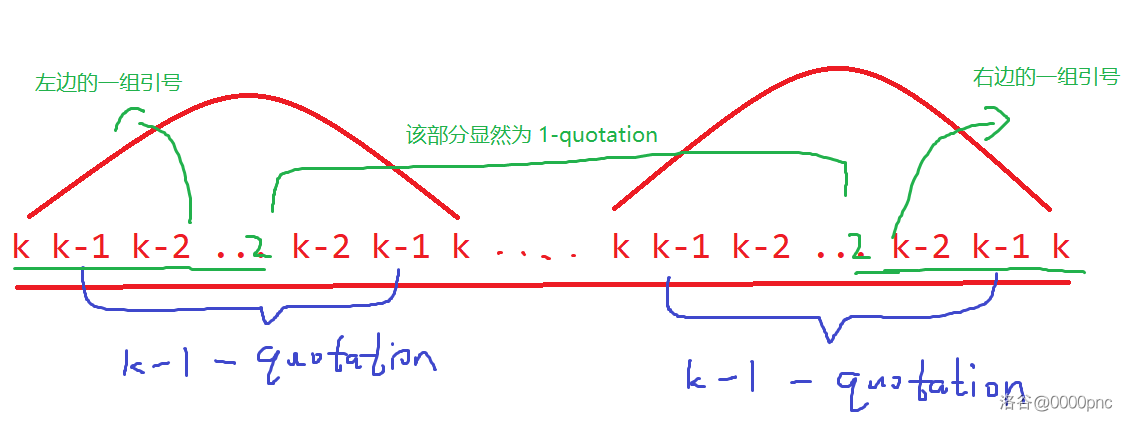
把首尾的 $\{k,k-1,k-2,\cdots,2\}$ 单独拎出来，那中间的显然是一个 1-quotation 序列（图中未写出“序列”），这样就符合 n-quotation 的定义了。

于是可以枚举答案 $x$，然后对于每个答案都可以利用这个性质 $\mathcal{O}(x)$ 判断是否合法（即：依次从头和尾删去 $x,x-1,x-2,\cdots,2$ 个引号，每次判断删除操作是否合法即可）。注意到答案的上界是 $\min(a_1,a_n)$，因此时间复杂度为 $\mathcal{O}(V^{2})$（或者 $\mathcal{O}(nV)$？）。

最后可能需要特判答案为 $1$ 的情况，这个也很好处理。

#include <bits/stdc++.h>
using namespace std;

int n, a[105], sm, tmp[105];

bool chk(int x) {
	for (int i = 1; i <= n; i++) tmp[i] = a[i];
	int l = 1, r = n, i;
	for (i = x; i > 1 && l <= r; i--) {
		if (tmp[l] < i) break;
		tmp[l] -= i; if (!tmp[l]) ++l;
		if (tmp[r] < i) break;
		tmp[r] -= i; if (!tmp[r]) --r;
	}
	return (l <= r && i == 1);
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]), sm += a[i];
	if (sm & 1) return printf("no quotation\n"), 0;
	for (int i = min(a[1], a[n]); i >= 2; i--) {
		if (chk(i)) return printf("%d\n", i), 0;
	}
	return printf(sm == 2 ? "1\n" : "no quotation\n"), 0;
}