自动搬运

查看原文

来自洛谷，原作者为

	岸芷汀兰 岸芷汀兰，郁郁青青。

搬运于2025-08-24 22:25:12，当前版本为作者最后更新于2021-07-03 11:01:57，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

一、题目：

洛谷原题

codeforces原题

二、思路：

这道题官方题解讲的非常好，我这里就当是简单的翻译一下官方的题解吧。

让我们从一条单独的河流 $p$ 开始。我们的目的是让这条河流的排名尽可能的靠前。显然，在从 $p$ 到根的路径上，我们都要选择 $p$ 作为汇合点的名字。假设通过这样的选择后，$p$ 的长度是 $L$。现在，问题变成了在其他汇合点上如何恰当地选择名字，使得尽可能少的河流比 $L$ 长。

如果一条河流比 $L$ 长，那我们就称这条河流是长的。否则，称这条河流是短的。我们的目标是最小化长河流的数目（等价于最小化短河流变成长河流的地点的个数）。让我们接下来考虑那些不包括 $p$ 的汇流点。

• 如果至少有一条将要进入该汇流点的河流是长的，那么我们就可以让它继续流（从而终止其他河流）。
• 如果所有的河流都是短的，那么我们要选择最短的河流让它继续流。

时间复杂度 $O(n^2)$——对于每个河流，我们都要执行上述过程。

现在，让我们致力于一次性计算出所有河流的答案。

对于每个河流 $p$，我们的目标是回答“如果我们在 $p$ 到根的路径上总是选择 $p$，那么我们需要至少形成多少个比 $L$ 长的河流”，这个问题等价于“我们需要至少形成多少个比 $L$ 长的河流”而不带有其他的限制。为了看到这一点，让我们采取最优策略来形成尽可能少的、比 $L$ 长的河流。然后考虑那些在 $p$ 到根的路径上、没有选择 $p$ 的汇流点，可以发现，如果我们在这些汇流点选择了 $p$，长河流的数目并不会增多。既然无论多少次选择 $p$，$p$ 的长度都不会长于 $L$，而且长河流的数目还有可能减少，那么我们当然可以在每个可以选择 $p$ 的汇流点选择 $p$。

所以我们需要对于每个 $L$，回答“至少需要形成多少个比 $L$ 长的河流”这个问题。我们将会以 $L$ 递增的顺序来一次性的回答所有问题。

假设当前处理到了长度 $L$，对于每个汇流点和每个叶子结点，它们都是以下三种状态的其中之一：

• 至少有一条将要进入该交汇点的河流是长的（叶子结点不可能处于这种状态）。
• 所有将要进入该交汇点的河流都是短的，但是流出该交汇点的河流将会变成长河流。
• 所有将要进入该交汇点的河流都是短的，并且流出该交汇点的河流也是短河流。

在第二种和第三种状态，根据贪心原则，我们选择最短的河流让它流出去。

让我们以 $L=0$ 开始。所有的叶子结点都处于状态 2，所有的汇流点都处于状态 1，共有 $N$ 条长河流。

当 $L$ 增长时，可能有一些点会从状态 2 变到状态 3，也可能有一些点会从状态 1 变到状态 2。还可能有一些点会直接从状态 1 变到状态 3。比如下面这张图：

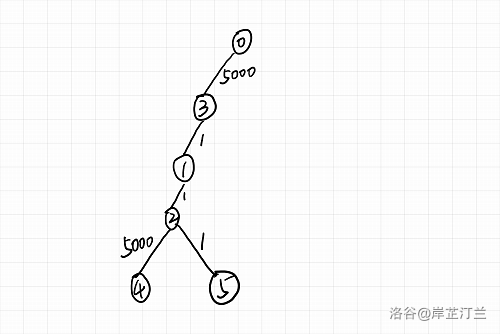
当 $L$ 从 $1$ 增长到 $5000$ 时，汇流点 2、1 都会从状态 1 变成状态 3。汇流点 3 会从状态 1 变成状态 2。

我们对于所有是状态 2 的节点维护一个小根堆，堆中保存的是二元组 $(l,x)$，表示要想把 $x$ 从状态 2 变成状态 3，$L$ 至少应该等于 $l$。每次从堆中取出最小的 $l$，把 $x$ 的状态更改为 3。再去检查 $x$ 的祖先有没有可能变状态（变成状态 2 的条件是所有儿子都是状态 3，但是别忘了特判直接从状态 1 蹦到状态 3 的情况）。由于一个点最多从状态 1 变到状态 2 一次，从状态 2 变到状态 3 一次，所以最终的时间复杂度是 $O(n\log n)$。

三、代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <queue>
#include <map>

using namespace std;
typedef pair<long long, int> PLI;
#define FILEIN(s) freopen(s, "r", stdin)
#define FILEOUT(s) freopen(s, "w", stdout)
#define mem(s, v) memset(s, v, sizeof s)

inline int read(void) {
    int x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
    while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
    return f * x;
}

const int MAXN = 1000005;
const long long INF = 1e17;

int n, m, head[MAXN], tot;
int v[MAXN], fa[MAXN], cnt[MAXN];
long long dp[MAXN], sum[MAXN];
string name[MAXN];
map<long long, int>ans;
map<long long, int>::iterator it;

struct Edge {
    int y, next;
    Edge() {}
    Edge(int _y, int _next) : y(_y), next(_next) {}
}e[MAXN];

priority_queue<PLI, vector<PLI>, greater<PLI> >q;

inline void connect(int x, int y) {
    e[++tot] = Edge(y, head[x]);
    head[x] = tot;
}

void dfs(int x, int father) {
    fa[x] = father;
    sum[x] = sum[father] + v[x];
    long long minn = INF;
    for (int i = head[x]; i; i = e[i].next) {
        int y = e[i].y;
        dfs(y, x);
        ++cnt[x];
        minn = min(minn, dp[y]);
    }
    if (minn == INF) dp[x] = v[x];
    else dp[x] = minn + v[x];
}

int main() {
    n = read(); m = read();
    for (int i = m + 1; i <= m + n; ++i) {
        cin >> name[i];
        int y = read(); v[i] = read();
        connect(y, i);
    }
    for (int i = 1; i <= m; ++i) {
        int y = read();
        v[i] = read();
        connect(y, i);
    }
    dfs(0, 0);
    int now = 0;
    long long L = 0;
    for (int i = m + 1; i <= m + n; ++i) {
        q.push({ dp[i], i });
        ++now; // 维护状态2的节点个数。
    }
    while (q.size()) {
        int x = q.top().second; long long l = q.top().first; q.pop();
        L = l;

        --now;
        --cnt[fa[x]];

        if (fa[x] && !cnt[fa[x]]) {
            x = fa[x];
            while (x && L >= dp[x]) { // 检查x的祖先们。
                --cnt[fa[x]];
                if (cnt[fa[x]] == 0) {
                    x = fa[x];
                }
                else break;
            }
            if (x && cnt[x] == 0 && L < dp[x]) {
                q.push({ dp[x], x });
                ++now;
            }
        }
        ans[L] = now + 1;
    }
    ans[INF] = 0; // 防止越界。
    for (int i = m + 1; i <= n + m; ++i) {
        it = ans.upper_bound(sum[i]); 
        --it; // 由于在求解的过程中，L的增长并不是连续的，所以我们要找最后一个小于等于sum[i]的L所对应的答案。
        cout << name[i] << " " << (*it).second << endl;
    }
    return 0;
}