自动搬运

查看原文

来自洛谷，原作者为

	Froggy 最初的一步，泪水之后再一次，雕刻的风景线，消逝在黄昏中的风，直到梦的最后。—— Clannad

搬运于2025-08-24 22:25:03，当前版本为作者最后更新于2020-10-31 18:48:30，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Sol 1：乱搞

爆搜/模拟退火/……

暴力求最大团，其实就是这题-> 外太空旅行

Sol 2：正经做法：

放到平面上，其实就有优秀的多项式做法了。

枚举最大团最远的点对，如果两点之间连一条直线，剩下的可用的点就被分到两个区域内。如果把这些点中不能同时被选的点连一条边，容易发现这是个二分图，因为区域内部的点之间不可能连边。

放个图更好理解一点：（两个黑点是钦定的最远点对）

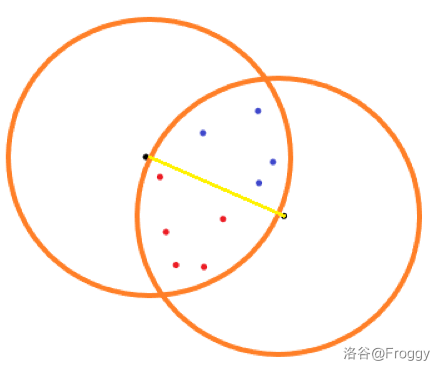
然后求二分图最大独立集即可。

时间复杂度应该的 $\mathcal{O}(n^{4.5})$ 的吧，反正常数极小跑的飞快。

code:

const int inf=0x3f3f3f3f;
#define N 155
namespace Maxflow{
	int cnt,S,T,dep[N],head[N],pre[N];
	struct Edge{
		int to,nxt,val;
	}edge[N*N<<1];
	void Clear(){
		memset(head,0,sizeof(head));
		cnt=1;
	}
	void add(int a,int b,int c){
		edge[++cnt]={b,head[a],c};
		head[a]=cnt;
	}
	void adde(int a,int b,int c){
		add(a,b,c),add(b,a,0);
	}
	queue<int> q;
	bool bfs(){
		memset(dep,0,sizeof(dep));
		dep[S]=1;
		q.push(S);
		while(!q.empty()){
			int u=q.front();
			q.pop();
			for(int i=head[u];i;i=edge[i].nxt){
				int v=edge[i].to;
				if(edge[i].val&&!dep[v]){
					dep[v]=dep[u]+1;
					q.push(v);
				}
			}
		}
		return dep[T]>0;
	}
	int dfs(int u,int limit){
		if(u==T)return limit;
		int flow=0;
		for(int &i=head[u];i;i=edge[i].nxt){
			int v=edge[i].to;
			if(dep[v]==dep[u]+1&&edge[i].val){
				int k=dfs(v,min(limit,edge[i].val));
				edge[i].val-=k;
				edge[i^1].val+=k;
				flow+=k;
				limit-=k;
			}
			if(!limit)break;
		}
		if(!flow)dep[u]=inf;
		return flow;
	}
	int Dinic(){
		memcpy(pre,head,sizeof(head));
		int maxflow=0;
		while(bfs()){
			maxflow+=dfs(S,inf);
			memcpy(head,pre,sizeof(head));
		}
		return maxflow;
	}
	bool vis[N];
	void dfs(int u){
		vis[u]=true;
		for(int i=head[u];i;i=edge[i].nxt){
			int v=edge[i].to;
			if(edge[i].val&&!vis[v])dfs(v);
		}
	}
	void Plan(){
		memset(vis,false,sizeof(vis));
		dfs(S);
	}
}
int n,D;
vector<int> ans;
struct Point{
	int x,y;
	Point(int _x=0,int _y=0){x=_x,y=_y;}
	Point operator -(const Point b){
		return Point(x-b.x,y-b.y);
	}
	int operator %(const Point b){
		return x*b.y-y*b.x;
	}
}p[N];
inline int Dis(Point &a,Point &b){
	return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
inline bool Left(Point a,Point b){
	return a%b<0;
}
inline bool Para(Point a,Point b){
	return a%b==0;
}
void Solve(int a,int b){
	static int type[N];
	static vector<int> res;
	res.clear();
	int tot=0,lim=Dis(p[a],p[b]);
	Maxflow::Clear();
	Maxflow::S=a,Maxflow::T=b;
	res.push_back(a),res.push_back(b);
	for(int i=1;i<=n;++i){
		type[i]=-1;
		if(i==a||i==b)continue;
		if(Dis(p[a],p[i])>lim||Dis(p[b],p[i])>lim)continue;
		
		if(Para(p[i]-p[a],p[b]-p[a])){
			res.push_back(i);continue;
		}
		
		type[i]=Left(p[i]-p[a],p[b]-p[a]);
	}
	for(int i=1;i<=n;++i){
		if(!~type[i])continue;
		type[i]==0?Maxflow::adde(a,i,1):Maxflow::adde(i,b,1);
	}
	for(int i=1;i<=n;++i){
		if(!~type[i])continue;
		for(int j=i+1;j<=n;++j){
			if(!~type[j])continue;
			if(type[i]^type[j]){
				if(Dis(p[i],p[j])>lim){
					type[i]==0?Maxflow::adde(i,j,1):Maxflow::adde(j,i,1);
				}
			}
		}
	}
	Maxflow::Dinic();
	Maxflow::Plan();
	for(int i=1;i<=n;++i){
		if(!~type[i])continue;
		if(type[i]^Maxflow::vis[i])res.push_back(i);
	}
	if(res.size()>ans.size()){
		ans=res;
	}
}
int main(){
	n=read(),D=read();
	for(int i=1;i<=n;++i){
		p[i].x=read(),p[i].y=read();
	}
	ans.push_back(1);
	for(int i=1;i<=n;++i){
		for(int j=i+1;j<=n;++j){
			if(Dis(p[i],p[j])<=D*D){
				Solve(i,j);
			}
		}
	}
	printf("%d\n",(int)ans.size());
	for(auto x:ans){
		printf("%d ",x);
	}
	printf("\n");
	return 0;
}