自动搬运

查看原文

来自洛谷，原作者为

	ytb2024 我是 闪避 ^_^

搬运于2025-08-24 22:24:54，当前版本为作者最后更新于2023-09-04 22:21:22，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

思路易懂，代码简单。

题目传送门

附：AT原题目

题意：开始有一个序列。在每一个时间，你从后往前将每个值变为它与它前面一个值的 $\max$。有一些询问，问你在一些时间的某个区间的和。

先将序列想象成一个矩阵。

下面是图：

经过观察几组数据的图可以发现，序列上每个点的区域行成了一个平行四边形，设第 $i$ 个平行四边形纵长为 ${\text{g1}} _ {i}$，横长为 ${\text{g2}} _ {i}$。

可以发现，$\mathrm{g1}$ 为 $i$ 与 $i-1 \sim 1$ 中第一个大于 $i$ 位置上值的坐标的差。例如上图中的 ${\text{g1}} _ {4} = 3$，因为第一个大于 $6$ 的是 $9$，${\text{g1}} _ {2} = 1$，因为第一个大于 $2$ 的是 $3$。

$\mathrm{g2}$ 为 $i+1 \sim n$ 中第一个大于等于 $i$ 位置上值的坐标与 $i$ 的差。例如上图中的 ${\text{g2}} _ {3} = 1$，因为第一个大于等于 $2$ 的是 $6$，${\text{g2}} _ {2} = 2$，因为第一个大于等于 $3$ 的是 $6$。

需要注意的是，$i$ 的前面如果没有比它大的，会形成一个三角行（图上那坨屎，后面再处理）。但如果 $i$ 的后面没有大于等于它的，我们可能要在 $n+1$ 这个点上设一个无穷大，防止没有上限。

用单调栈求解，时间复杂度 $\mathrm{O}\left(\mathrm{n}\right)$。

代码：

a[n+1]=mx+1,stk[++stp]=n+1;
per(i,1,n)
{
	while(a[i]>a[stk[stp]])stp--;
	r[i]=stk[stp];
	if(a[i]==a[stk[stp]])stk[stp]=i;
	else stk[++stp]=i;
}
stp=0;
rep(i,1,n)
{
	while(stp&&a[i]>=a[stk[stp]])stp--;
	if(!stp)stk[++stp]=i;
	else l[i]=stk[stp],stk[++stp]=i;
}

转换为矩阵问题，考虑如何用数据结构维护 $n \times n$ 个点。

一个显然的地方，对于一个等腰直角三角形，我们可以暴力加点，$\frac{n ^ {2}}{2}$ 个点只需要 $n$ 次操作。例如上图中的那坨屎，就可以暴力处理。考虑如何处理平行四边形。

下面是图：

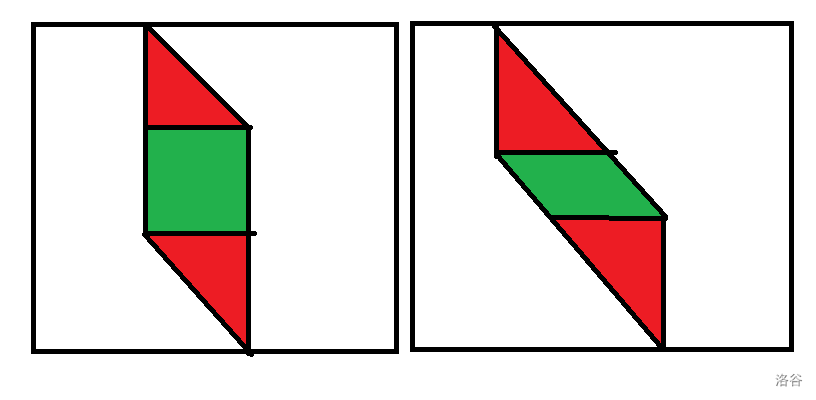
可以发现上图为两种情况。

第一种，上面下面分别一个三角形，中间一个正方形。用前面的方法处理三角形，正方形不用管。

第二种，上面下面分别一个三角形，可以直接处理。平行四边形可以采用让询问左移的方法。

代码：

rep(i,1,n)mx=max(dep,r[i]-i),gg2[i]=r[i]-i;
rep(i,1,n)
{
	if(!l[i])
	{
		gg1[i]=dep-gg2[i]+1;
		rep(j,gg1[i]+1,dep)w1[j].push_back(upd{j-gg1[i]-1+i,a[i]});
	}
	else gg1[i]=i-l[i];
}
rep(i,1,n)if(gg1[i]>=gg2[i])rep(j,1,gg2[i])w1[j].push_back(upd{i+j-1,a[i]}),w1[gg1[i]+j].push_back(upd{i+j-1,-a[i]});else rep(j,1,gg1[i])w2[j].push_back(upd{i-j+1,a[i]}),w2[gg2[i]+j].push_back(upd{i-j+1,-a[i]});
rep(i,1,dep)
{
	for(auto y:w1[i])add(y.id,y.add,0);
	for(auto y:w2[i])add(y.id+n,y.add,1);
	for(auto y:ques[i-1])ans[y.id]=que(y.r,0)-que(y.l-1,0)+que(y.r-i+1+n,1)-que(y.l-i+n,1);
}

注：设 $\mathrm{mx}$ 为 $\max \left( {\text{g2}} _ {i} \right)$，对与层数大于 $\mathrm{mx}$ 的，特殊处理一下。

代码：

rep(i,1,n)b[i]=max(a[i],b[i-1]),add(i,b[i],2);
rep(i,mx,n)for(auto y:ques[i])ans[y.id]=que(y.r,2)-que(y.l-1,2);

时间复杂度 $\mathrm{O}\left(\mathrm{n} \log{\mathrm{n}}\right)$。

Record