自动搬运

查看原文

来自洛谷，原作者为

	stoorz **

搬运于2025-08-24 22:24:39，当前版本为作者最后更新于2020-09-16 16:51:16，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

UPD on 2020.11.23

感谢神仙验题人

nend](https://www.luogu.com.cn/user/11788) CCCCOrz。

这道题的 idea 最初来源于 P3514 [POI2011]LIZ-Lollipop，那道题利用其它性质可以 $O(n)$ 预处理答案，$O(1)$ 回答。并不支持修改操作。

然后有一天和 QuantAsk 讨论这题的时候想出了支持修改的 $O(m\log n)$ 做法，然后就有了这道题 /fad。

看到有人说这道题卡常 /kk，将数据范围开这么大是因为 $O(m\log^2 n)$ 做法常数实在是太小了，我尝试构造了很多数据都可以轻松跑过，所以最终只能在数据范围下手。

有神仙写线段树被卡常，但我和验题人的递归版线段树都是可以在不加 O2 下 $2s$ 跑过的。至于有神仙写 Splay。。。那我真的感到抱歉了 /kel。

std 是树状数组，所以常数小一点，我尝试了很多次，在不加 O2 下都可以在 $1s$ 内跑过。

题意简述

给出一个长度为 $n$ 的 $1,2$ 序列。要求支持单点修改，查询和为 $k$ 且左端点尽量小的区间。

算法 1

枚举左端点，发现在左端点不断向右扫描的过程中，右端点的位置也一定单调不减。所以不用每次重新开始扫描右端点，在上一次扫描的基础上继续向右即可。

时间复杂度 $O(nm)$，期望得分 $20pts$。

算法 2

将原序列做前缀和，设做前缀和后的序列为 $s$，问题转化为求最小的两个位置 $i,j$ 使得 $s_j-s_i=k$。

对于修改操作，相当于将序列 $s$ 的一段后缀全部加上一个数；对于查询操作，可以枚举左端点，二分出右端点，如果这一段区间的和为 $k$ 即为答案。

时间复杂度 $O(nm\log n)$ 或 $O(nm\log^2 n)$，取决于是在数据结构内二分还是二分套数据结构。写的好看一些或许可以拿到 $20pts$。

甚至没有算法 1 优秀。

算法 3

在算法 2 中，容易发现我们二分出的每一段区间和要么是 $k$，要么是 $k+1$。因为如果和大于 $k+1$ 的话，右端点向左移动一位和肯定不小于 $k$。

假设我们二分出的两个区间为 $[l,r_1]$ 和 $[l+1,r_2]$，且这两个区间的和均为 $k+1$，那么：

• $a_l$ 一定等于 $2$，否则 $[l+1,r_1]$ 就是一个合法的和为 $k$ 的区间。

• $a_{r_1}$ 一定等于 $2$，否则 $[l,r_1-1]$ 就是一个合法的和为 $k$ 的区间。

• $r_2=r_1+1$，因为 $\sum^{r_1}_{i=l} a_i=\sum^{r_2}_{i=l+1}a_i-\sum^{r_2}_{i=r_1+1}a_i+a_l$，而 $a_l=2$，当 $r_2>r_1+1$ 时， $\sum^{r_2}_{i=r_1+1}a_i=2$ 当且仅当 $r_2=r_1+2$ 且 $a_{r_1+1}=a_{r_1+2}=1$，此时区间 $[l,r_1+1]$ 就是一个合法的和为 $k$ 的区间。

最后一点换句话说，黄色部分的和一定等于蓝色部分的和，而蓝色部分的和为 $2$，那么只有当 $r_2=r_1+1$ 且 $a_{r_2}=2$ 时才满足条件。

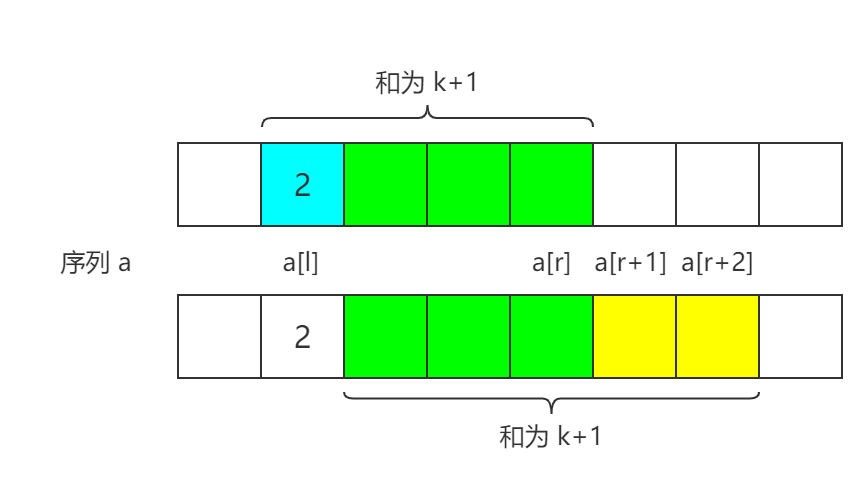
那如果再加入一个区间 $[l+2,r_3]$，那么就有 $a_{l+1}=a_{r2}=2,r_3=r_2+1$。我们发现，只要接下来有一个位置不是 $2$ 了，那么一定存在一个和为 $k+1$ 的区间，也就是答案区间与连续的 $2$ 的个数有关。

那么我们用数据结构维护前缀和，对于每一次询问，二分出从位置 $1$ 开始和不小于 $k$ 的区间 $[1,p]$。然后再用数据结构求出位置 $1$ 和位置 $p$ 后连续的 $2$ 的个数，假设分别为 $cnt1$ 个和 $cnt2$ 个，

• 当 $cnt1<cnt2$ 时，区间 $[2+cnt1,p+cnt1]$ 即为答案。

• 当 $cnt1\geq cnt2$ 时，区间 $[1+cnt2,p+cnt2]$ 即为答案。

可以手写小数据来理解。

那么我们需要解决两个问题：

1. 如何找到第一个前缀和不小于 $k$ 的位置。

2. 如何求出一个位置后面有多少个连续的 $2$。

对于问题 1，直接采用二分+数据结构即可。对于问题 2，依然可以二分长度，假设为 $len$，那么只需要判断区间 $[p,p+len-1]$ 的和是否为 $2\times len$ 即可。

采用树状数组或者线段树实现均可。

时间复杂度 $O(m\log^2 n)$，期望得分 $50pts$。

算法 4

可以在算法 3 的基础上，在数据结构内二分。可以省掉一个 $\log$。

树状数组二分或线段树二分均可，后者写法不优美可能会被卡。

时间复杂度 $O(m\log n)$，期望得分 $100pts$。