自动搬运

查看原文

来自洛谷，原作者为

	Cute__yhb **

搬运于2025-08-24 22:24:31，当前版本为作者最后更新于2025-07-12 11:25:53，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

前言

社贡掉没了，来写篇题解。

这题是山东三轮省集某天模拟赛搬的题。

思路

注意到 $t=2$ 时的字典序限制是从 $n$ 到 $1$ 的，这启发我们倒着想，将建楼转化成拆楼。

一开始，所有楼都是建好的，每一次操作，我们要找到当前能拆的楼中编号最大的，把它拆掉。

对于一座楼，如果能被拆，一定满足以下条件。

• 对于所有楼按八连通建边的图中，它不是割点。

• 它能到达无穷远。

对于第一条限制来说，显然，如果该图不是联通图，一定不合法，否则一定存在方案满足条件。

先来解决第二条限制。

直接建图空间肯定会炸，考虑把一部分点表示出来。

对于一座楼，如果它四联通的空地里有到达无穷远的，那它也能到达无穷远。

考虑到下一个限制是八连通，所以，先把每个楼八联通的空地存下来，判断时只判断四联通的那些点，这样，点的个数就是 $O(n)$ 量级的了。

可以先找到一个能到达无穷远的空地，比如横坐标最小的，然后找出该点所在的空地的连通块，则该块都能到达无穷远。

在拆楼的过程中，每个空地最多一次改变是否能到达无穷远的状态，所以这一部分直接暴力搜索这个楼四周的空地即可。时间复杂度 $O(n)$。

这样，就有了一种 $O(n^2)$ 的暴力：每次都把图建出来，用 Tarjan 找出割点。

现在来解决第二条限制。

因为是网格图，所以割点只会有以下几种情况。

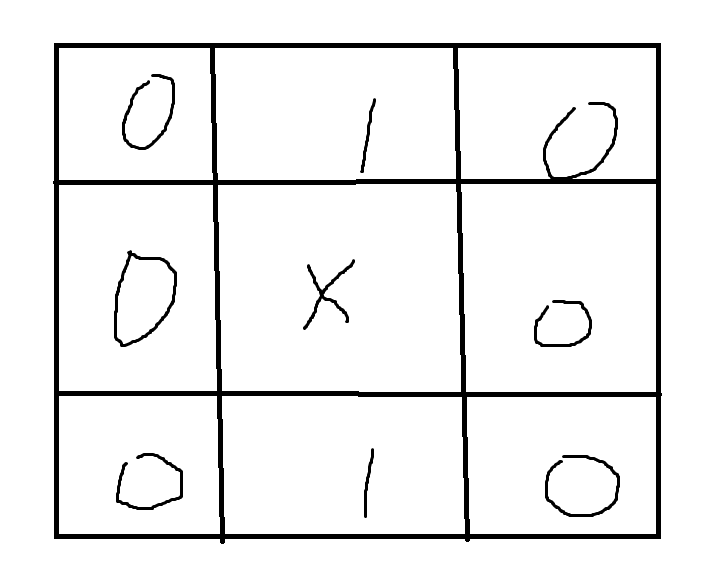
图中，$1$ 是楼，$0$ 是空地，$x$ 是判断是否是割点的楼。

如果图中的 $0$ 属于同一连通块，此时拆掉 $x$ 的话，上下的 $1$ 就不连通了，所以这时 $x$ 是割点。

将此图翻转同理。

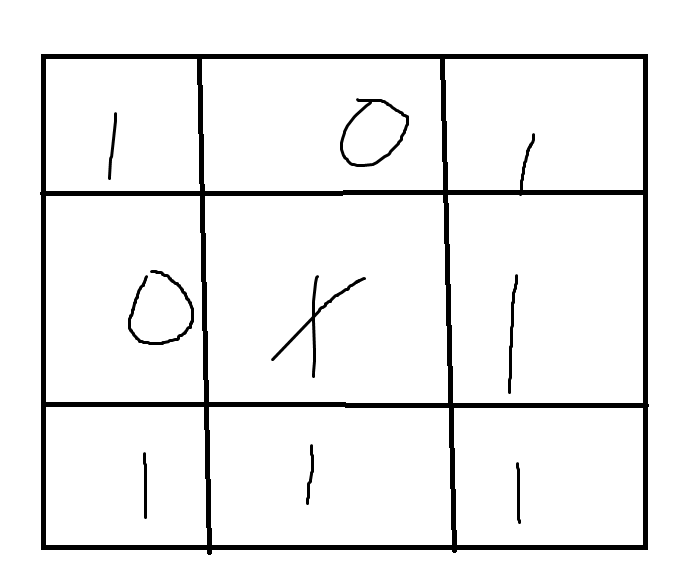
如果图中的 $0$ 属于同一连通块时，同理，$x$ 是割点。

初始化时顺便处理每个空地所处的连通块即可。

当拆楼时，所影响到只有被拆掉的楼四周的空地连通块周围的楼的状态。

因为改变是否是割点的只有被删的楼八连通的楼，所以时间复杂度同样是 $O(n)$。

找编号最大的楼可以用 set，维护每个点的状态可以用 map。复杂度多带一个 log。

代码

不知道是不是实现的问题，我感觉这题稍微有点卡常。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define F(i,l,r) for(int i=l;i<=r;i++)
#define UF(i,r,l) for(int i=r;i>=l;i--)
#define p_q priority_queue
#define pb push_back
#define mk(a,b) make_pair(a,b)
#define pii pair<int,int> 
#define ve vector
#define endl '\n'
#define fi first
#define se second
#define INF 0x3f3f3f3f
#define lowbit(x) (x&(-x))
// #pragma GCC optimize("O3")
int dx[]={0,1,0,-1,0,1,1,-1,-1};
int dy[]={0,0,1,0,-1,1,-1,1,-1};
int n,T;
struct node{
	int x,y;
}a[150005],b[1919811];
map<pii,int> f,vis;
int cnt=0,_=0;
void dfs(int x,int y){
	if(!vis.count(mk(x,y))||!vis[mk(x,y)]) return ;
	_++;
	vis[mk(x,y)]=0;
	for(int i=1;i<=8;i++){
		int xx=x+dx[i];
		int yy=y+dy[i];
		dfs(xx,yy);
	}
}
set<int>s;
inline bool check(int x,int y);
bool chk(int x,int y);
inline void full(int x,int y,int col,int F){
	if(!f.count(mk(x,y))){
		return ;
	}
	if(f[mk(x,y)]==col||f[mk(x,y)]==1) return ;
	f[mk(x,y)]=col;
//	full(x+1,y,col,F);
//	full(x-1,y,col,F);
//	full(x,y+1,col,F);
//	full(x,y-1,col,F);
	for(register int i=1;i<=4;i++){
		int xx=x+dx[i];
		int yy=y+dy[i];
		full(xx,yy,col,F);		
	}
	if(!F) return ;
	for(register int i=1;i<=4;i++){
		int xx=x+dx[i];
		int yy=y+dy[i];
		if(vis.count(mk(xx,yy))&&vis[mk(xx,yy)]!=0){
			if(chk(xx,yy)){
				s.insert(vis[mk(xx,yy)]);
			}else{
				if(s.find(vis[mk(xx,yy)])!=s.end()){
					s.erase(s.find(vis[mk(xx,yy)]));
				}
			}
		}
	}
}
int ans[150005],live[150005];
int tot=0,root;
int F[9];
inline bool check(int x,int y){
	F[1]=f[mk(x-1,y-1)];
	F[2]=f[mk(x-1,y)];
	F[3]=f[mk(x-1,y+1)];
	F[4]=f[mk(x,y-1)];
	F[5]=f[mk(x,y+1)];
	F[6]=f[mk(x+1,y-1)];
	F[7]=f[mk(x+1,y)];
	F[8]=f[mk(x+1,y+1)];
	if((F[1]==1||F[2]==1||F[3]==1)&&(F[6]==1||F[7]==1||F[8]==1)&&F[4]==F[5]&&F[5]<0) return 0;
	if(F[2]<0&&F[7]==F[2]&&(F[1]==1||F[4]==1||F[6]==1)&&(F[3]==1||F[5]==1||F[8]==1)) return 0;
	if(F[2]==F[4]&&F[4]<0&&F[1]==1&&(F[6]==1||F[7]==1||F[8]==1||F[5]==1||F[3]==1)) return 0;
	if(F[7]==F[5]&&F[5]<0&&F[8]==1&&(F[1]==1||F[4]==1||F[6]==1||F[3]==1||F[2]==1)) return 0;
	if(F[3]==1&&(F[1]==1||F[4]==1||F[6]==1||F[7]==1||F[8]==1)&&F[2]==F[5]&&F[5]<0) return 0;
	if(F[6]==1&&(F[3]==1||F[5]==1||F[8]==1||F[2]==1||F[1]==1)&&F[7]==F[4]&&F[4]<0) return 0;
	return 1&&(F[2]==-1||F[4]==-1||F[5]==-1||F[7]==-1);
}
bool chk(int x,int y){
	return check(x,y);
}
int main(){
//	freopen("c.in","r",stdin);
//	freopen("c.out","w",stdout);
	cin>>n>>T;
	for(register int i=1;i<=n;i++){
		live[i]=1;
		scanf("%d%d",&a[i].x,&a[i].y);
		vis[mk(a[i].x,a[i].y)]=1;
		f[mk(a[i].x,a[i].y)]=1;
		for(int j=1;j<=8;j++){
			int xx=a[i].x+dx[j];
			int yy=a[i].y+dy[j];
			if(!f.count(mk(xx,yy))){
				cnt++;
				b[cnt].x=xx;
				b[cnt].y=yy;
				f[mk(xx,yy)]=0;
			}
		}
	}
	dfs(a[1].x,a[1].y);
	if(_!=n){
		cout<<"NO";
		return 0;
	}
	cout<<"YES\n";
	_=1;
	for(register int i=2;i<=cnt;i++){
		if(b[i].x<b[_].x) _=i;
	}
	full(b[_].x,b[_].y,-1,0);
	_=-1;
	for(register int i=1;i<=cnt;i++) {
		if(f[mk(b[i].x,b[i].y)]==0){
			_--;
			full(b[i].x,b[i].y,_,0);
		}
	}
	for(register int i=1;i<=n;i++){
		vis[mk(a[i].x,a[i].y)]=i;
		if(chk(a[i].x,a[i].y)){
			s.insert(i);
		}
	}
	for(_=n;_;_--){
		set<int>::iterator __=s.end();
		__--;
		ans[_]=*__;
		vis[mk(a[*__].x,a[*__].y)]=0;
		f[mk(a[*__].x,a[*__].y)]=0;
		full(a[*__].x,a[*__].y,-1,1);
		int x=a[*__].x,y=a[*__].y;
		for(register int i=1;i<=8;i++){
			int xx=x+dx[i];
			int yy=y+dy[i];
			if(vis.count(mk(xx,yy))&&vis[mk(xx,yy)]!=0){
				if(chk(xx,yy)){
					s.insert(vis[mk(xx,yy)]);
				}else{
					if(s.find(vis[mk(xx,yy)])!=s.end()){
						s.erase(s.find(vis[mk(xx,yy)]));
					}
				}
			}
		}
		s.erase(__);
	}
	for(register int i=1;i<=n;i++) printf("%d\n",ans[i]);
    return 0;
}