自动搬运

查看原文

来自洛谷，原作者为

	AK_Dream 菜的没边

搬运于2025-08-24 22:24:31，当前版本为作者最后更新于2020-12-08 16:09:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题解

题目实际在求这样一个东西：给定一棵树和边权，你可以在树中加上一条长为 $S$ 的有向边

对于每个叶子节点问：是否能构造出一条从根节点出发以该节点为终点的长为 $K$ 的路径

设有一个叶子节点 $x$

情况1

根到 $x$ 的路径长等于 $K$

那显然答案就是 Yes

情况2

走了一次附加的有向边使得路径长为 $K$

考虑这条有向边的终点在哪里：由于走过这条有向边之后还要从它的终点走到 $x$，所以有向边的终点一定要是 $x$ 的一个祖先

记点 $p$ 的深度是 $d_p$，那么假设走了一条 $p\rightarrow q$ 的有向边，总长度就是 $d_p+S+(d_x-d_q)$

其中，$p$ 是树上的任意一个非叶子节点，$q$ 必须是 $x$ 的祖先

要判断是否有 $p,q$ 满足 $d_p+S+(d_x-d_q)=K$，可以考虑枚举 $q$，这样就确定了 $d_x-d_q$，预处理出 $d_p+S$ 可以取哪些值(存在一个 bool 数组里)，如果存在某个 $p$ 使得 $d_p+S=K-(d_x-d_q)$ 那么 $x$ 的答案就是 Yes

一个例子

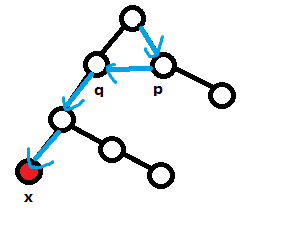
情况3

当然，可能可以走很多次附加的有向边(在一个环上一直绕)

如果一条有向边可以走很多次，那么必须满足它的终点是起点的祖先

又因为终点要是 $x$ 的祖先，所以现在需要找到这样一条路径 $p\rightarrow q$：

满足 $d_x+t*(d_p-d_q+S)=K$ ($t$ 为一个正整数)

其中 $q$ 是 $x$ 的祖先，$p$ 是 $q$ 子树中一个非叶子节点

在dfs时，每到一个非叶子节点就再把以它为根的子树遍历一遍，把所有合法的 $d_p-d_q+S$ 存在 bool 数组里，并在回溯时清除贡献

枚举 $K-d_x$ 的所有约数，判断是否有满足条件的 $d_p-d_q+S$ 即可

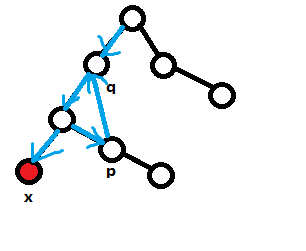
时间复杂度 $O((n+m)^2+m\sqrt{K})$

#include <bits/stdc++.h>
#define N 20005
using namespace std;
typedef long long ll;

template <typename T>
inline void read(T &num) {
	T x = 0, ff = 1; char ch = getchar();
	for (; ch > '9' || ch < '0'; ch = getchar()) if (ch == '-') ff = -1;
	for (; ch <= '9' && ch >= '0'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ '0');
	num = x * ff;
}

int n, ccf, K, S, a[N], d[N];
int head[N], pre[N<<1], to[N<<1], sz;
int ok[1000005], ok2[1000005], ans[N];

inline void addedge(int u, int v) {
	pre[++sz] = head[u]; head[u] = sz; to[sz] = v;
	pre[++sz] = head[v]; head[v] = sz; to[sz] = u;
}

void dfs1(int x, int fa) {
	if (d[x]+S <= 1000000 && x <= ccf) ok[d[x]+S]++;
	for (int i = head[x]; i; i = pre[i]) {
		int y = to[i];
		if (y == fa) continue;
		d[y] = d[x] + a[y];
		dfs1(y, x);
	}
} 

void dfs3(int x, int fa, int rt, int v) {
	if (x > ccf) return;
	int now = d[x] - d[rt] + S;
	if (now <= 1000000) ok2[now] += v;
	for (int i = head[x]; i; i = pre[i]) {
		int y = to[i];
		if (y != fa) dfs3(y, x, rt, v);
	}
}

int stk[N], top;

void solve(int x) {
	if (d[x] == K) {
		ans[x] = 1; return;
	}
	for (int i = 1; i <= top; i++) {
		int y = stk[i];
		int v = d[x] - d[y];
		if (v <= K && ok[K-v]) ans[x] = 1;
	}
	if (d[x] < K) {
		int v = K - d[x];
		for (int i = 1; i * i <= v; i++) {
			if (v % i == 0) {
				if (ok2[i] || ok2[v/i]) ans[x] = 1;
			}
		}
	}
}

void dfs2(int x, int fa) {
	if (x > ccf) {
		solve(x);
		return;
	}
	stk[++top] = x;
	dfs3(x, fa, x, 1);
	for (int i = head[x]; i; i = pre[i]) {
		int y = to[i];
		if (y != fa) dfs2(y, x);
	}
	dfs3(x, fa, x, -1);
	top--;
}

int main() {
	read(n); read(ccf); read(K); read(S); S++;
	swap(ccf, n); n += ccf;
	for (int i = 1, p; i <= n; i++) {
		read(p); read(a[i]); a[i]++;
		addedge(p, i);
	}
	dfs1(0, 0);
	dfs2(0, 0);
	for (int i = ccf + 1; i <= n; i++) puts(ans[i]?"YES":"NO");
	return 0;
}