自动搬运

查看原文

来自洛谷，原作者为

	rui_er 九万里风鹏正举

搬运于2025-08-24 22:24:24，当前版本为作者最后更新于2020-10-11 19:06:13，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

破事水：IOI2020 结束后就想要写这题，但是 spj 当时是锅的，修好后我就秉承鸽子的良好品德一直咕到了现在。

因为 CSP2020 考的有点自闭，所以来做一道 IOI 真题放松一下。

题意简述：构造一个无向图，使得任意两个点之间路径个数与题目给出的相同。

思路：

注：因为洛谷与其他 oj（包括 IOI 官方）的评测方式不同，本题解代码以洛谷为准，在其他 oj 可能无法直接取的 AC，请额外注意。

首先，如果一个图中的一个连通块，拥有多于一个环，那么这种情况肯定不符合题意。为啥呢？画个图理解一下。

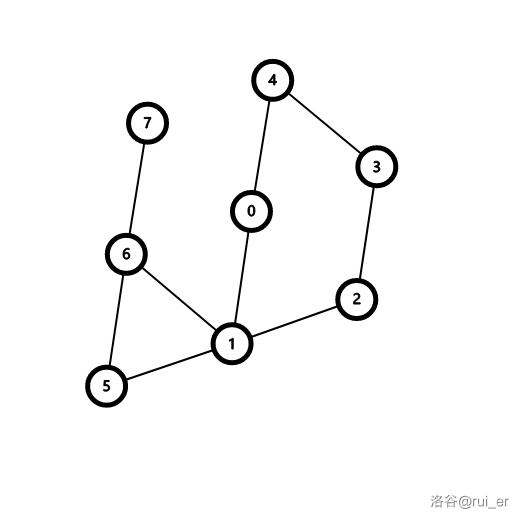
以这张图上 $4\rightarrow 6$ 的路径为例，共有如下情况：

1. $4\rightarrow 0\rightarrow 1\rightarrow 6$
2. $4\rightarrow 0\rightarrow 1\rightarrow 5\rightarrow 6$
3. $4\rightarrow 3\rightarrow 2\rightarrow 1\rightarrow 6$
4. $4\rightarrow 3\rightarrow 2\rightarrow 1\rightarrow 5\rightarrow 6$

因为跨过了两个环，路径条数显然多于三个。

我们得到了构造的初步方向：原图必须是一个由树或基环树组成的森林。

接着找规律：

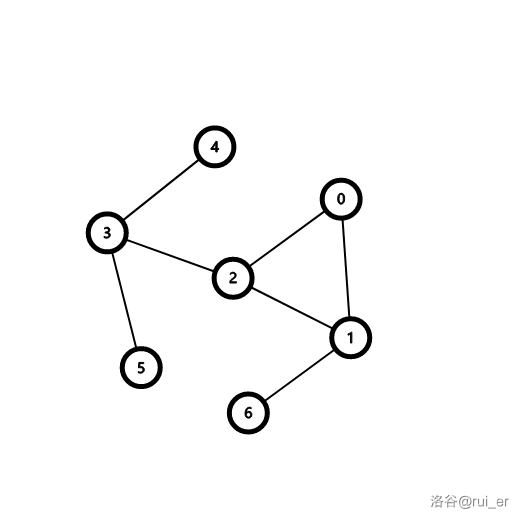
对于这棵基环树，通过手推，发现：

1. 对于任意两个点（比如 $2,4$），它们之间的路径如果全在环外，那么它们之间有且仅有一条路径。
2. 对于任意两个点（比如 $6,3$），它们之间的路径如果至少有一条边一定在环上，那么它们之间有两条路径。

换句话说，就是把所有环上的边先删掉，如果还在连通块内，就只有一条边。

可以看到，如果题目中要求 $u,v$ 之间有三条路径，此时无解。

我们先 dfs 一遍求出连通块，如果连通块内存在要求有三条路径的边，就直接判掉。如果有两个点之间路径要求为零，也可以判掉。剩下的情况就分为两种：树和基环树。

对于连通块内只要求两两之间有一条路径，将其中一个点和连通块内其他所有点相连即可。对于基环树，我们先不考虑路径数为二的边，在剩下的路径数为一的边里面再次 dfs 求出环外的连通块，按照相同方式连接后，每个环外连通块取一个点，将这些点依次连城环即可。

至此我们便得到了正解。

代码：

//By: Luogu@rui_er(122461)
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;

void build(vector<vector<int> > b);

int n, ma, vis[N];
vector<int> block, edge, circle; // 分别为连通块、基环树上的树边和基环树上的环 
vector<vector<int> > graph, res;
void add(int u, int v) {res[u][v] = res[v][u] = 1;}
void dfs(int u) {
//	printf("DFS %d\n", u);
	vis[u] = 1;
	block.push_back(u);
	for(int v=0;v<n;v++) {
		ma = max(ma, graph[u][v]);
		if(!vis[v] && graph[u][v]) dfs(v);
	}
}
void dfsCircle(int u) {
	vis[u] = 2;
	edge.push_back(u);
	for(int v=0;v<n;v++) if(vis[v] == 1 && graph[u][v] == 1) dfsCircle(v);
}
int construct(vector<vector<int> > p) {
//	puts("CONSTRUCT");
	graph = p; n = p.size(); res.resize(n);
	for(int i=0;i<n;i++) res[i].resize(n);
	for(int i=0;i<n;i++) {
		if(vis[i]) continue;
		ma = 1; block.clear(); dfs(i);
//		printf("ROUND %d DFS ENDED WITH MAX=%d\n", i, ma);
		if(ma == 3) return 0;
		int sz = block.size();
		for(int j=1;j<sz;j++) {
			for(int k=0;k<j;k++) {
				if(!graph[block[j]][block[k]]) return 0;
			}
		}
		if(ma == 1) for(int j=1;j<sz;j++) add(block[0], block[j]);
		else {
			circle.clear();
			for(int _=0,j=block[_];_<sz;_++,j=block[_]) {
				if(vis[j] != 1) continue;
				edge.clear();
				dfsCircle(j);
//				puts("DFSCIRCLE ENDED");
				int sz2 = edge.size();
				for(int k=1;k<sz2;k++) {
					for(int l=0;l<k;l++) {
						if(graph[edge[k]][edge[l]] != 1) return 0;
					}
					add(edge[0], edge[k]);
				}
				circle.push_back(edge[0]);
//				printf("CIRCLE ADDED %d\n", edge[0]);
			}
			if(circle.size() <= 2) return 0;
			int sz3 = circle.size();
			for(int j=0;j<sz3;j++) add(circle[j], circle[(j+1)%sz3]);
		}
	}
	build(res);
	return 1;
}/*

void build(vector<vector<int> > b) {
	puts("BUILD");
	for(int i=0;i<b.size();i++) {
		for(int j=0;j<b[i].size();j++) printf("%d ", b[i][j]);
		puts("");
	}
}
int main() {
	vector<vector<int> > a = vector<vector<int> >
							({vector<int>({1, 1, 2, 2}), vector<int>({1, 1, 2, 2})
							, vector<int>({2, 2, 1, 2}), vector<int>({2, 2, 2, 1})});
	build(a);
	printf("CONSTRUCT ENDED WITH RETURN VALUE %d\n", construct(a));
	return 0;
}*/