自动搬运

查看原文

来自洛谷，原作者为

	dead_X Still we rise

搬运于2025-08-24 22:23:54，当前版本为作者最后更新于2022-09-15 08:46:43，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

将序列以长度为 $C$ 分块，那么答案要么在一块里面，要么是一块后缀加一块前缀。

一块里面的很好算，就是对这个区间求最大子段和。

一块后缀加一块前缀比较难算，记 $A_i$ 为这一块后 $i$ 个数的和，$B_i$ 为下一块前 $i$ 个数的和，我们要实现一个直角三角形区域的最大值查询：

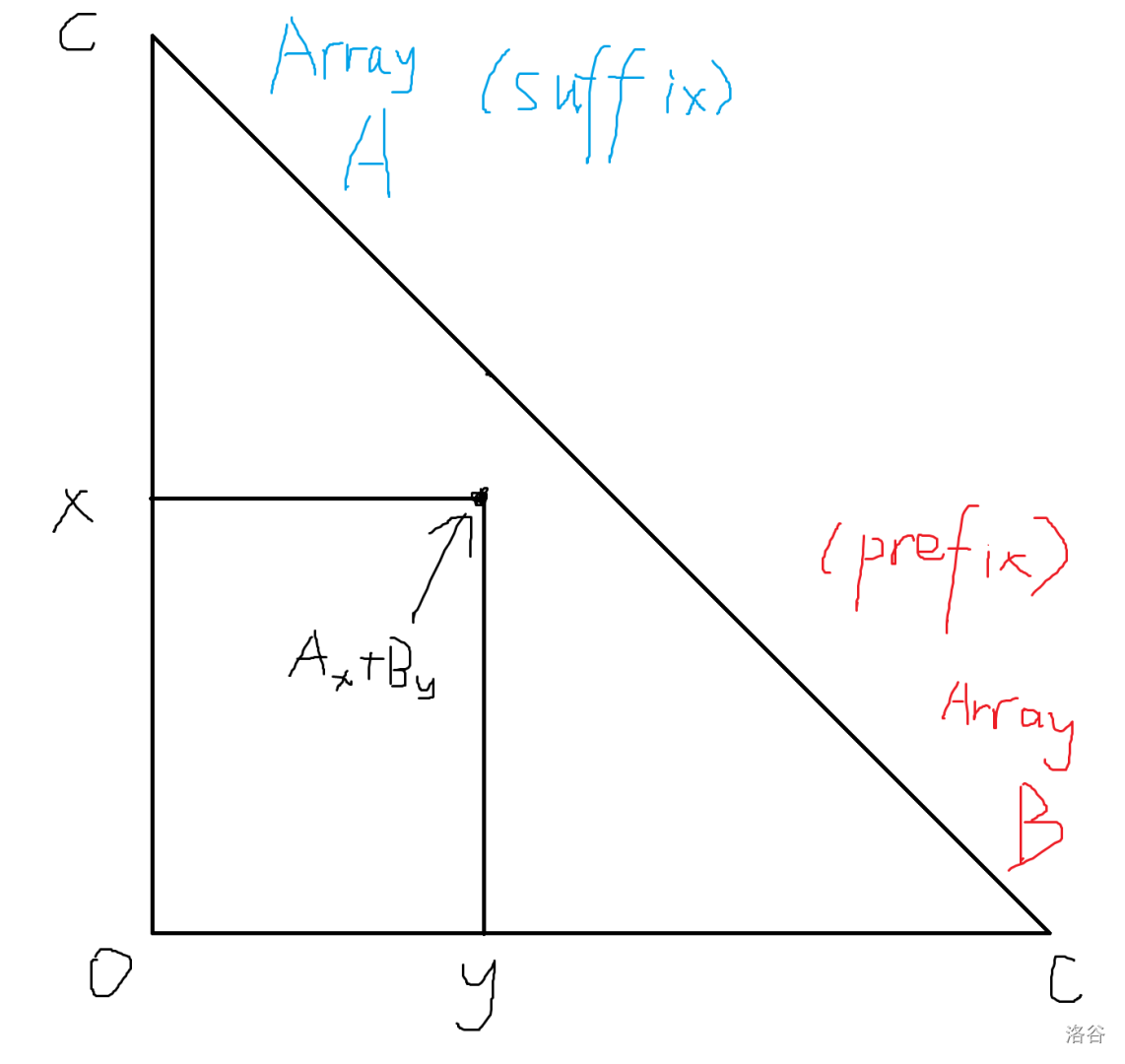
问题转化为 $A$ 数组后缀加，$B$ 数组后缀加，全局所有点最大值。

看到这种等腰直角三角形求值的套路，首先可以通过这种方式来做：

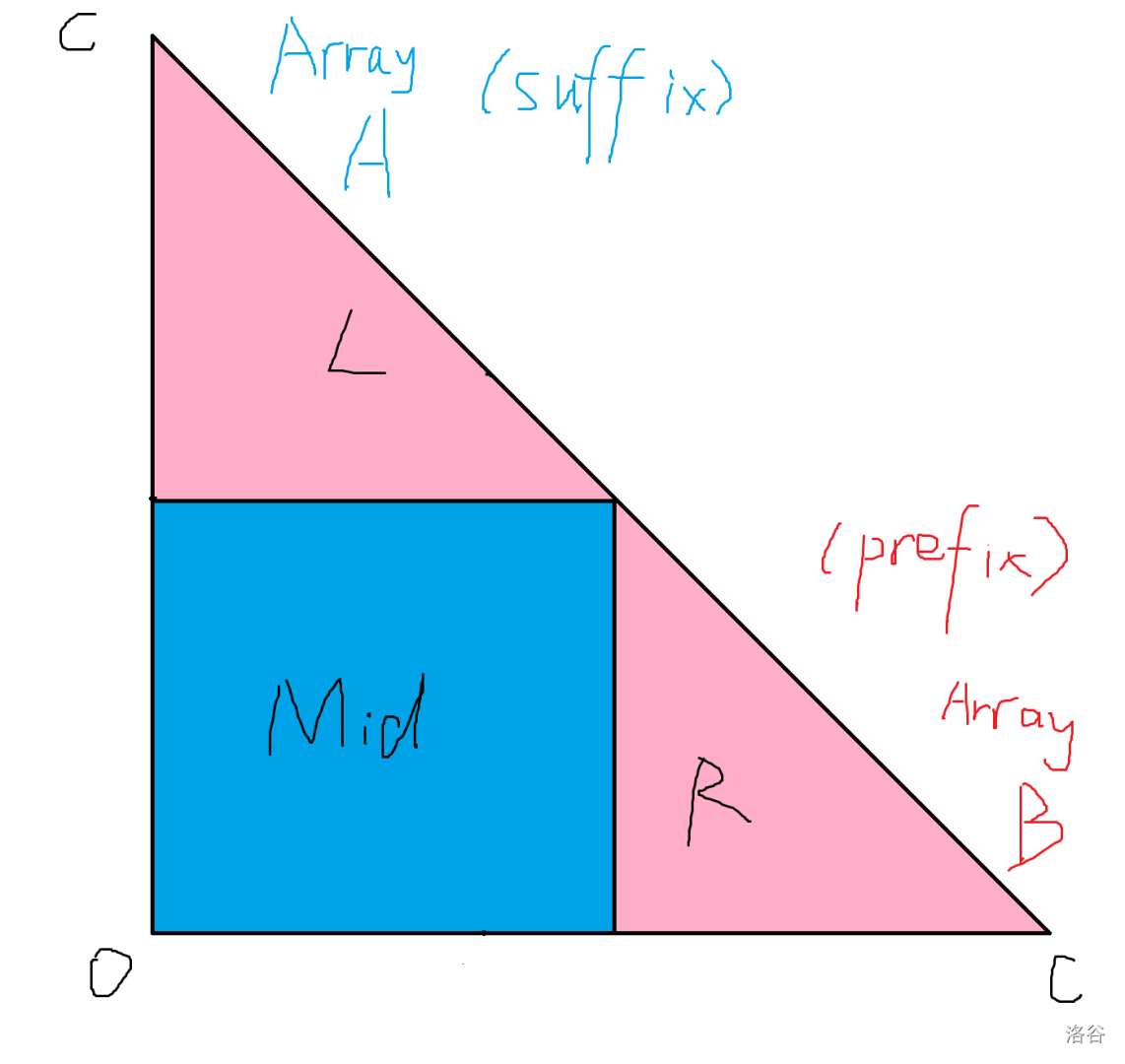
即将三角形拆成两个更小的三角形，然后中间转为矩形求解，矩形求解可以根据两个三角形的信息反推。

看到这个结构就不难想到线段树了吧，我们对于每个节点维护横向最大值，纵向最大值，三角形最大值，合并是平凡的。

于是这样 $A$ 数组和 $B$ 数组的区间修改就可以用带懒标记的线段树做了。

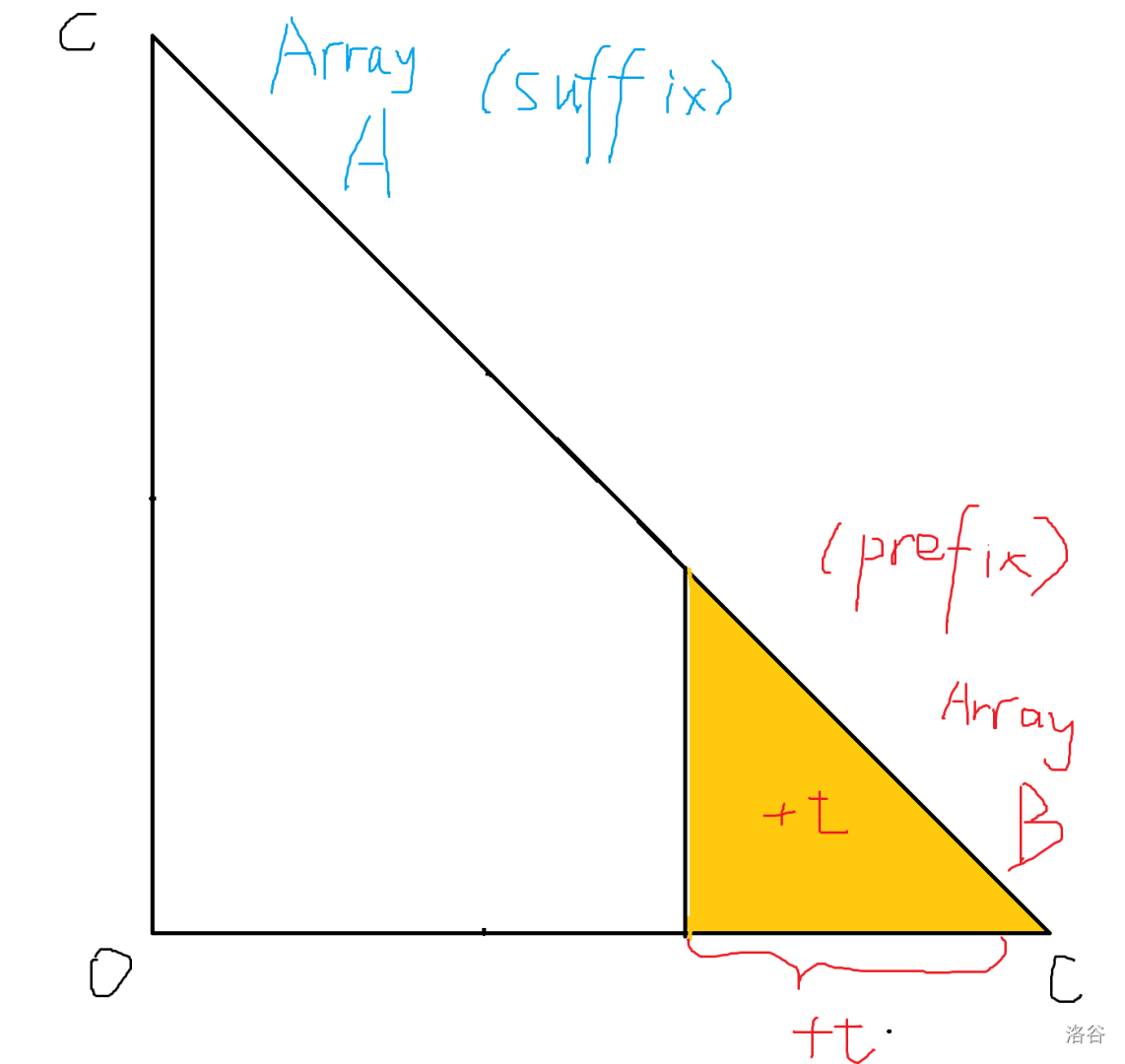
我们递归到线段树上对应这几个区间的节点，将三角形最大值和横向/竖向最大值加上 $t$，然后再把信息合并起来即可。

Corner case 是一块只能取最后若干个，另一块只能取最前若干个。

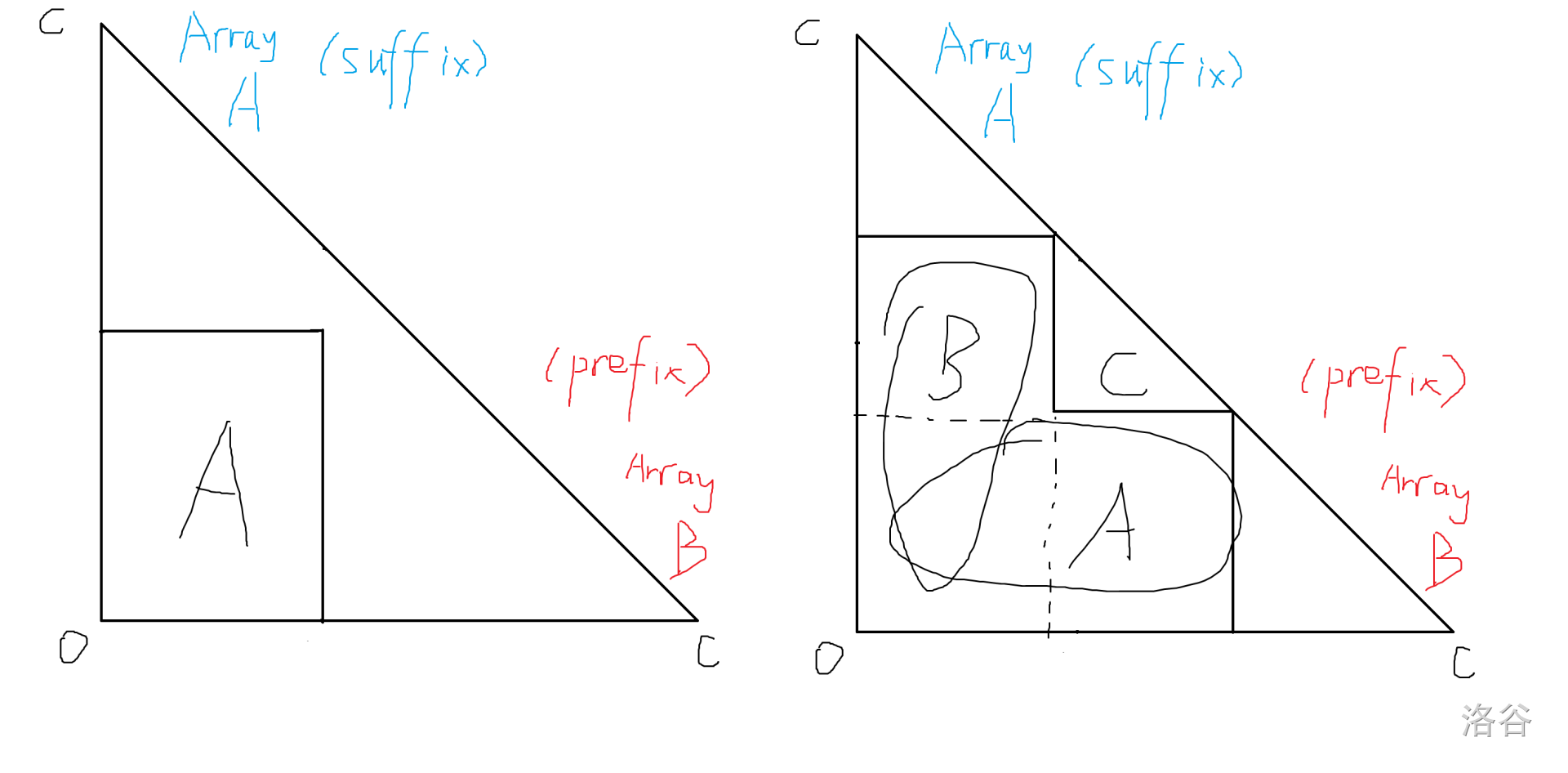
我们也能拆成若干个询问，所以这题做完了。

时间复杂度 $O(m\log n)$，比较卡常，如果不想卡常可以去 gym 上交，如果被卡常了可以洗洗脸多交几发。

一些卡常小技巧：

• 能 build 就不要一个一个 update，把 $n\log n$ 尽可能消掉。
• 线段树不用开到 $4n$，可以计算一个上界。
• 对于 merge 比较慢的信息，可以单侧递归直接返回就单侧递归。
• 快读快写可能没什么用。
• 开 inline 有用。
• 少开 long long 有用。

要代码私聊。