自动搬运

查看原文

来自洛谷，原作者为

	幻影星坚强 この世で造花より綺麗な花は無いわ 何故ならば総ては嘘で出来ている

搬运于2025-08-24 22:23:46，当前版本为作者最后更新于2020-11-13 11:40:25，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

时隔多月重见此题，发现没有题解发现其实考场上的思路是对的把重心当成根就好了（）

• 思路

我们一开始并不能确定根节点是哪里所以我们先不去管它。

假设我们找到了一个根节点，并且它的度数为2，我们考虑怎么做。

一个显然的想法，我们每次从它的左右两个子树中选取深度最大的一个，因为总路程可以看成一个子树->根->另一个子树，而因为对于每一个子树里我们选取的深度都是不增的，所以一个子树->根与根->另一个子树的值都是不增的，总路程也是不增的。

现在的问题是如何找到这样的一个根。我们发现每两次操作都会使两棵子树大小各减一，而如果一个子树的大小与另一颗子树的大小相差2及以上，那么在最后就只会剩下根->子树，我们不能保证有一个合适的方案使其在路程小于等于之前的同时走的路程不增，所以最好的办法是让一个子树的大小与另一颗子树的大小相差1及以下，所以我们可以知道选择的点是重心。

以上是重心度数为2的情况下，我们可以选择重心为根，接下来考虑重心的度数是3该怎么处理。

因为重心的子树大小不会超过 $\left\lfloor\dfrac{n}{2}\right\rfloor$，所以如果其中有一个子树大于等于其他两个子树的和，那么它的大小一定是$\left\lfloor\dfrac{n}{2}\right\rfloor$，我们可以将剩下的两棵子树看成一棵子树来处理。这就成了度数为2的情况。

而如果最大的子树大小小于剩余两个的和，那么我们每次从非上一次选的子树中选择一个最大的（第一次可任意选），这样也能保证路程递减，如图

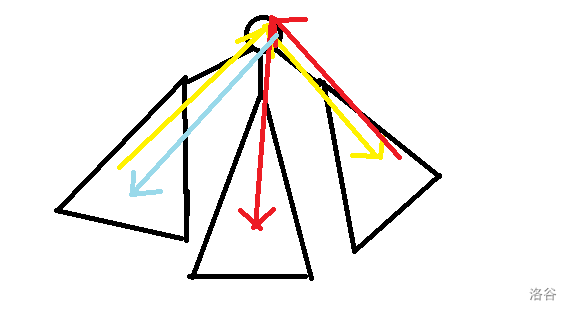
一开始先从黄边走到第三棵子树如果接下来走蓝边的话就和度数为2的情况下一样必然是不增的，假如走红边我们可以用反证法，如果它的长度比第一棵子树里的黄边大，那么它们的长度顺序为第一棵子树黄$<$边第二棵子树红边$<$第三棵子树黄边，那么第一棵子树黄边则是最短的，那么之前第一棵子树的黄边肯定不会选到，选择的节点会在第二棵和第三棵子树之间，他们的深度一定大于第一棵子树的黄边，所以不成立，即第一棵子树黄$>$边第二棵子树红边。

我们可以按照这样的方式进行选择，每次都会在最大的子树和剩下的两个子树里交替选择，而剩下的两个子树也可以交替选择，所以剩余两个子树的和$-$最大的子树大小会不断变小($\Delta$前者的大小始终会$\ge$$\Delta$后者的大小),最终他们会相等,这时就可以将剩余两个子树合并起来,成为度数为2的情况

（有一处细节在代码里）

#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
int hoursRequired(int X, int Y);
int attractionsBehind(int X, int Y);
std::vector<int> createFunTour(int N, int Q);
const int N = 1e5 + 10;
int siz[N], dep[N];
int b[3], tot;
std::vector<pair<int, int> >q[7];
std::vector<int>ans;
int root;
void merge()
{
	while(q[2].size())
	{
		q[1].push_back(q[2][q[2].size() - 1]);
		q[2].pop_back();
	}
	sort(q[1].begin(), q[1].end());
}

void br2()
{
	while(q[0].size() + q[1].size())
	{
		pair<int, int>now = q[0][q[0].size() - 1];
		q[0].pop_back();
		ans.push_back(now.second);
		q[0].swap(q[1]);
	}
	ans.push_back(root);
}

int C(int a, int b, int c)
{
	return a + b + c - max(a, max(b, c));
}
int nn;
void br3()
{
	if(q[0].size() == nn / 2)
	{
		merge();
		if(q[0].size() < q[1].size())
		q[0].swap(q[1]);
		br2();
		return;
	}
	int flag = 0;
	while(1)
	{
		int to = flag;
		for (int i = flag + 1; i <= 2; ++ i)
		{
			if(q[i][q[i].size() - 1] >= q[to][q[to].size() - 1])
			to = i;
		}
		flag = 1;
		pair<int, int>maxs = q[to][q[to].size() - 1];
		ans.push_back(q[to][q[to].size() - 1].second);
		q[0].swap(q[to]);
		q[0].pop_back();
		if(max(max(q[0].size(), q[1].size()), q[2].size()) == C(q[0].size(), q[1].size(), q[2].size()))
		{
			int now = 0;
			if(q[0].size() < q[1].size())
			q[0].swap(q[1]), now = 1;
			if(q[0].size() < q[2].size())
			q[0].swap(q[2]), now = (now == 0 ? 2 : now);
			if(now != 0)
			{
				if(maxs < q[((now - 1) ^ 1) + 1][q[((now - 1) ^ 1) + 1].size() - 1])
				ans.push_back(q[((now - 1) ^ 1) + 1][q[((now - 1) ^ 1) + 1].size() - 1].second), q[((now - 1) ^ 1) + 1].pop_back();
			}
        //此处注意，假如合并的两个子树中有一个是最近选择的，另一个子树的最大深度大于这个，那么要再选择一次，否则合并后下一次选择的深度就不能保证不增了
			merge();
			if(now == 0)
			q[0].swap(q[1]);
			br2();
			return;
		}
	}
	ans.push_back(root);
}

std::vector<int> createFunTour(int n, int Q)
{
	nn = n;
	for (int i = 0; i < n; ++ i)
	{
		siz[i] = attractionsBehind(0, i);
	}
	for (int i = 0; i < n; ++ i)
	{
		if(siz[i] > (n >> 1) && siz[i] < siz[root])
		root = i;
	}
	for (int i = 0; i < n; ++ i)
	{
		if((dep[i] = hoursRequired(root, i)) == 1)
		{
			b[tot] = i;
			++ tot;
		}
	}
	-- tot;
	for (int i = 0; i < n; ++ i)
	{
		if(i != root)
		{
			int to = 0;
			for (int j = 1; j <= tot; ++ j)
			{
				if(hoursRequired(b[j], i) <= dep[i])
				to = j;
			}
			q[to].push_back(make_pair(dep[i], i));
		}
	}
	for (int i = 0; i <= tot; ++ i)
	{
		sort(q[i].begin(), q[i].end());
		printf("%d\n", q[i][0].second);
	}
	if(tot == 1)
	{
		if(q[0].size() < q[1].size())
		q[0].swap(q[1]);
		br2();
	}
	else
	{
		if(q[0].size() < q[1].size())
		q[0].swap(q[1]);
		if(q[0].size() < q[2].size())
		q[0].swap(q[2]);
		br3();
	}
	return ans;
}