自动搬运

查看原文

来自洛谷，原作者为

	a___ 这个家伙很蒻，什么也没有留下qwq

搬运于2025-08-24 22:23:36，当前版本为作者最后更新于2020-08-10 17:08:55，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

update(20/8/18):感谢@loveJYdalao指出错误。

---

算法标签：$\color{#FFFFFF}\colorbox{#E74C3C}{\small\texttt{树上dp}}\ \color{#FFFFFF}\colorbox{#E74C3C}{\small\texttt{贪心}}$

---

这题其实很好写，就是dp状态不太好想。

前置芝士：一个数列的中位数小于等于 $x$ $\Leftrightarrow$ 一个数列有至少 $\left\lfloor\dfrac{len}{2}\right\rfloor+1$ 个数小于等于 $x$。

记 $\operatorname{val}(u,v)$ 表示边 $(u,v)$ 上的边权（或者叫做军队战斗力）。

首先，显然没有无解的情况，因为如果每条边权都置为 $1$，无论如何都不会有人造反。

然后，由于以上性质我们发现对于一条边的边权 我们只关心其是否大于两端点点权，于是
设 $f_{u,0/1}$ 表示
当 $\operatorname{val}(\operatorname{fa}(u),u)\leq a_u\ \ /\ \ \operatorname{val}(\operatorname{fa}(u),u)> a_u$ 时 以点 $u$ 为根的 子树内 满足条件的 边权和的 最大值。
设 $g_{u,0/1}$ 表示
当 $\operatorname{val}(\operatorname{fa}(u),u)\leq a_{\operatorname{fa}(u)}\ \ /\ \ \operatorname{val}(\operatorname{fa}(u),u)> a_{\operatorname{fa}(u)}$ 时 $\operatorname{fa}(u)$ 的子树 $u$，包括边 $(\operatorname{fa}(u),u)$， 边权和的最大值。

举个例子：

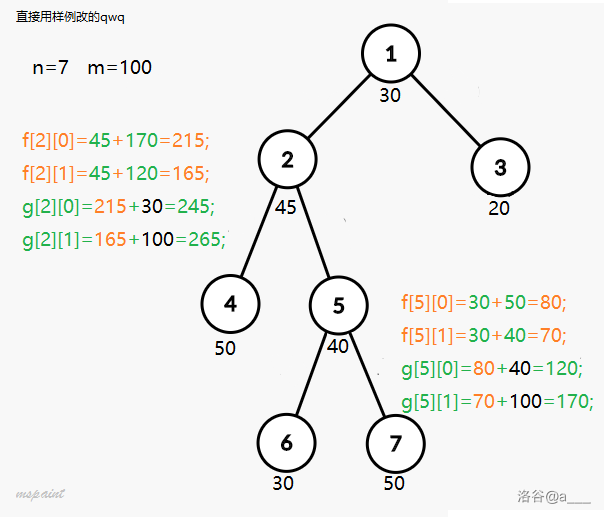
以点 $5$ 为例，其周围有 $3$ 条边，则应存在 $2$ 条边边权小于等于 $40$。当边 $(2,5)$ 边权小于等于 $40$ 时，向下可以有一条边权大于 $40$，所以 $f_{5,0}=30+50$。

显然，如果我们以点 $1$ 为根dfs，最后答案为 $f_{1,0}$。

接下来是状态转移。

1. 已经算出 $\forall v\in \operatorname{son}(u)\ \ \ \ g_{v,0/1}$，求 $f_{u,0/1}$：
   考虑贪心。我们先选所有 $g_{v,0}$，即使所有到儿子的边的边权都小于点 $u$ 点权。对于 $f_{u,0}$ ，此时可以有 $\operatorname{du}(u)-\left(\left\lfloor\dfrac{\operatorname{du}(u)}{2}\right\rfloor+1\right)$ 条边的边权大于点 $u$ 点权；对于 $f_{u,1}$ ，此时可以有 $\operatorname{du}(u)-\left(\left\lfloor\dfrac{\operatorname{du}(u)}{2}\right\rfloor+1\right)-1$ 条边的边权大于点 $u$ 点权。设允许的边权大于 $a_u$ 的边数为 $k$，我们从大到小枚举 $k$ 个 $g_{v,1}-g_{v,0}$，即贪心地考虑将小于 $a_u$ 的边换成大于 $a_u$ 的边即可。
2. 已经算出 $f_{u,0/1}$，求 $g_{u,0/1}$：
   分类讨论：
   1. $a_u<a_{\operatorname{fa}(u)}$
      1. $g_{u,0}$
         1. $a_u<\operatorname{val}(\operatorname{fa}(u),u)\leq a_{\operatorname{fa}(u)}$
         2. $\operatorname{val}(\operatorname{fa}(u),u)\leq a_u<a_{\operatorname{fa}(u)}$
      2. $g_{u,1}$
         1. $a_u<a_{\operatorname{fa}(u)}<\operatorname{val}(\operatorname{fa}(u),u)\leq m$
   2. $a_u=a_{\operatorname{fa}(u)}$
      直接并入1或3
   3. $a_u>a_{\operatorname{fa}(u)}$
      1. $g_{u,0}$
         1. $\operatorname{val}(\operatorname{fa}(u),u)\leq a_{\operatorname{fa}(u)} <a_u$
      2. $g_{u,1}$
         1. $a_{\operatorname{fa}(u)}<\operatorname{val}(\operatorname{fa}(u),u)\leq a_u$
         2. $a_{\operatorname{fa}(u)}<a_u<\operatorname{val}(\operatorname{fa}(u),u)\leq m$

综上：

$$g_{u,0}=\begin{cases}\max\{f_{u,0}+a_u,f_{u,1}+a_{\operatorname{fa}(u)}\}&a_u\leq a_{\operatorname{fa}(u)}\\f_{u,0}+a_{\operatorname{fa}(u)}&a_u>a_{\operatorname{fa}(u)}\end{cases} $$$$g_{u,1}=\begin{cases}f_{u,1}+m&a_u\leq a_{\operatorname{fa}(u)}\\\max\{f_{u,0}+a_u,f_{u,1}+m\}&a_u>a_{\operatorname{fa}(u)}\end{cases} $$

然后从下向上dp即可。

注意到当 $\operatorname{du}(u)\leq 2$ 时，无论如何不可能出现 $\operatorname{val}(\operatorname{fa}(u),u)>a_u$。此时，需特判将 $f_{u,1}$ 置为 $-\inf$。

AC代码