自动搬运

查看原文

来自洛谷，原作者为

	囧仙 你做东方鬼畜音MAD，好吗？

搬运于2025-08-24 22:23:28，当前版本为作者最后更新于2020-07-18 14:20:29，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目大意

有两个黑点，围成了一个圈。你可以通过以下操作扩充这个圈。

• 在两个点之间加入一个白点，并翻转这两个点的颜色。
• 删除一个白点，同时翻转它相邻的两个点的颜色。

翻转的含义是，将白色的点变成黑色，将黑色的点变成白色。

每次操作时，都必须保证操作后点的个数不小于 $2$ 。你可以进行无数次操作。现在经过若干次操作后，得到了一个大小为 $n$ 的圈。接着任取某个位置断开，会形成一个链。

同时，可能有 $m$ 个约束条件。第 $i$ 个约束条件 $(p_i,c_i)$ ，表示这条链的第 $p_i$ 个点应该是 $c_i$ 颜色的。其中，$c_i=0$ 表示该点为黑色， $c_i=1$ 表示该点为白色。

询问最多可以得到多少个满足条件的不同的链。由于可能结果太大，你只需要输出它对 $998244353$ 取模的结果。

两个链不同，当且仅当存在一个位置的点颜色不同。

题解

$\textbf{Subtask 1}\ n,m\le 16$

直接暴力操作，并判断是否符合条件即可。复杂度$\mathcal O(2^n\times n)$ 。

$\textbf{Subtask 2}\ n\le 10^6,m\le 5\times 10^3$

首先，让我们证明一个小结论：黑点的个数总为偶数个。

这个结论非常简单。考虑每次加点操作，如果左右两个点同色，那么黑点个数的变化量为$\pm2$；如果异色，那么相当于交换了两点，数量不变。由于初始时候，黑点数量为 $0$ ，因此任何时候黑点的数量都应该是偶数。

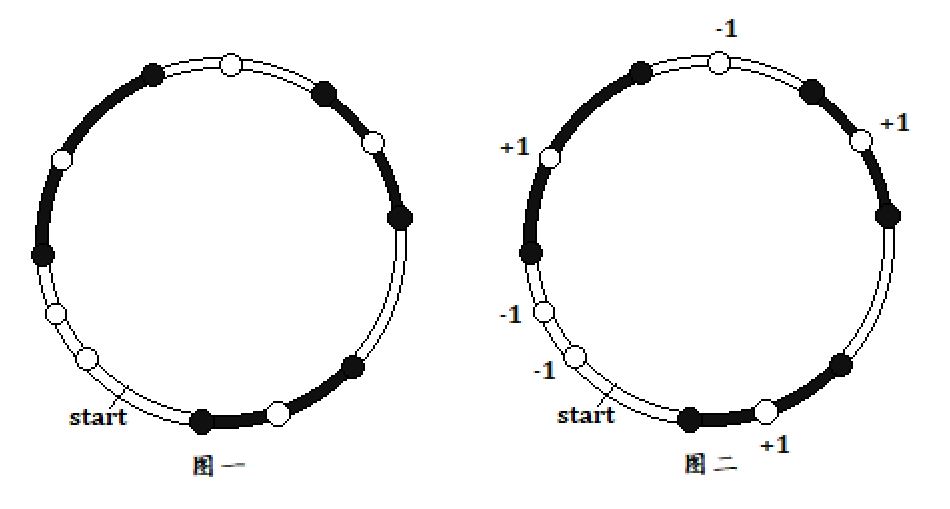
不妨设当前一共有 $p$ 个黑点，则这些黑点将圆弧划分为了 $p$ 段。我们对其进行染色。（如图 $1$ )

我们对圆弧进行染色：白色、黑色、白色……由于只有偶数段圆弧，所以每两个弧之间的颜色不同。

我们将黑色弧上的白点赋值为 $+1$ ，白色弧上的白点赋值为 $-1$ （如图 $2$）。统计所有白点的权值和 $S$ 。由于黑白弧可以交换，所以白点的权值和亦能为 $-S$ 。下面讨论两种操作对 $S$ 的影响。

• 当加入点的两侧都是黑点时，黑点变为白点。由于该操作不会影响其他点的权值，且这三个点权值相同。于是 $S\gets S\pm 3$ 。

• 当加入的点两侧都是白点时，白点变为黑点。显然，新加入的白点的权值与原先两点的权值相反。因此，$S\gets S\pm 3$。

• 当加入的点两侧的点的显色相异时，不妨设其中白点权值为 $a$ 。插入后，原先两侧的点位置交换，原来的白点交换后权值变为了 $-a$。新的点权值与该白点相同，亦为 $-a$ 。于是，$S\gets S-3\times a$。

对于删点操作，由于其是加点操作的互逆操作，因此 $S$ 的变化量也为 $3$ 的倍数。可以这样简要证明：

假设删去一个白点后，重新在该位置重新加入白点，此时 $S$ 不变；而加入白点，$S$ 的变化为 $3$ 的倍数，因此删点操作， $S$ 的变化量亦为 $3$ 的倍数。

初始时，$S=\pm 2$ 。因此终止状态的权值和 $S'$ 必有 ：

$$S'\not \equiv 0 \pmod 3$$

在开头，我们已经证明黑点的个数必为偶数。下证任何一个符合这两个条件的状态，都能由初始状态转移而来。

由于 $S' \not \equiv 0 \pmod 3$ ，因此无论何时都有至少一个白点。我们不断删去白点，直到只剩下两个点，其中也必有白点。同时，由于黑点个数为偶数，所以只有可能有 $0$ 个黑点，即初始状态。因此，从任何满足这两个条件的状态都能仅通过删点回到初始状态。又由于加点操作是删点的逆操作，因此我们只需要按照删点的顺序倒过来操作，就一定能获得该状态。

于是，我们可以用 $\rm dp$ 计算出方案总数。

由于最终我们会给圆环断链，因此就相当于提前给大小为 $n$ 的圆环的每个点编了号。不妨任取一个点开始，编为 $1,2,3\cdots$ 我们设计状态 $dp_{i,j,k}$，表示前 $i$ 个点，黑点个数$\mod 2=j$ 且 $S\mod 3=k$ 的方案总数。于是我们能够得到转移方程：

$$dp_{i,j,k}=\begin{cases} dp_{i-1,0,(k+2)\mod 3}+dp_{i-1,1,k} & j=0\cr dp_{i-1,1,(k+1)\mod 3}+dp_{i-1,0,k} & j=1\end{cases}$$

由于黑白可以交换，所以我们可以钦定第一个点处在白弧上。每讨论一个黑点，黑白弧的情况就会交换。初始时，$dp_{1,0,1}=dp_{1,1,0}=1$，其他的 $i=1$ 的情况都为 $0$ 。答案为 $dp_{n,0,1}+dp_{n,0,2}$。

关于限制条件的问题，我们只需要计算到限制点的时候，舍去不合法的转移方法。如限制点 $a$ 为白点，我们就要舍弃点 $a-1$ 转移到黑点的情况；限制点为白点同理可推。

$\textbf{Subtask 3}\ n\le 10^9,m=0$

如果你已经写出了上面两个$\rm Subtask$的任意一种，经过简单打表，你会发现，设 $f(x)$ 为 $n=x,m=0$ 时的结果，有：

$$f(x)=\begin{cases}1 & x=2 \cr f(x-1)\times 2+1 & x\text{为奇数} \cr f(x-1)\times 2-1 &x\text{为偶数}\end{cases} $$

至于这个式子怎么计算，最简单的方法，就是直接矩阵乘法……当然，你也可以考虑分治。

首先我们能够发现，

$$\begin{aligned}f(2k)&=f(2k-1)\times 2-1\cr&=(f(2(k-1))\times 2+1)\times 2-1\cr&=f(2(k-1))\times 4+1\end{aligned} $$

不妨设 $g(x)=f(2\times x)$ 。则 $g(1)=1,g(n)=4\times g(n-1)-1$。

假设我们要计算 $g(x)$ 用 $g(2)$ 表示的结果，那么我们只需要计算出 $g(\lfloor\frac{x}{2}\rfloor)$ 用 $g(2)$ 表示的结果，稍加修改就能推出用 $g(\lfloor\frac{x}{2}\rfloor)$ 表示 $g(x)$ 的结果。

当然，如果你数学功底足够好，你或许能直接推导出通项公式（

时间复杂度：$\mathcal O(\log_2n)$。

$\textbf{Subtask 4}\ n\le 10^{18},m\le 5\times 10^3$

让我们回到 $\text{Subtask 2}$ 的做法。

很显然，每个点的状态只与上个点有关，因此我们能够压缩掉第一维。

我们能够发现，该式可以矩阵加速递推。具体而言，我们设计一个 $1\times 6$ 的向量矩阵，其中第$(j\times 3+k+1)$ 列表示$dp_{i,j,k}$；然后设计一个转移矩阵，使用矩阵快速幂进行加速转化。

初始矩阵：

$$\begin{bmatrix}0 & a & 0 & b & 0 & 0\end{bmatrix}$$

其中，当点 $1$ 限制为白点时， $a=1$ ，否则 $a=0$ ；

其中，当点 $1$ 限制为黑点时， $b=1$ ，否则 $b=0$ 。

转移矩阵：

$$\begin{bmatrix} 0 & 1 & 0 & 1 & 0 & 0 \cr 0 & 0 & 1 & 0 & 1 & 0 \cr 1 & 0 & 0 & 0 & 0 & 1 \cr 1 & 0 & 0 & 0 & 0 & 1 \cr 0 & 1 & 0 & 1 & 0 & 0 \cr 0 & 0 & 1 & 0 & 1 & 0 \cr \end{bmatrix}$$

$\rm PS:$实际计算转移矩阵的时候，完全可以直接用 $\rm dp$ 式子生成，而不需要手推。

时间复杂度：$\mathcal O(m\times k^3\times \log _2 \frac{n}{m})$。其中，$k$为矩阵大小，即 $k=6$ 。

参考代码

$\text{Subtask 1}$，暴力代码：

#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l;i<=r;i++)
#define dn(l,r,i) for(int i=l;i>=r;i--)
using namespace std;

typedef long long LL;
const int INF =2147483647;
int qread(){
    int w=1,c,ret;
    while((c=getchar())> '9'||c< '0')
    w=(c=='-'?-1:1); ret=c-'0';
    while((c=getchar())>='0'&&c<='9')
    ret=ret*10+c-'0';
    return ret*w;
}
map<int,int> T;
bool chk(int n,int t){
    dn(n-1,2,i){
        int x=(t&-t),p=T[x];
        if(x==0) return false;
        if(p==i) t^=1,t^=(1<<i-1),t-=1<<p; else
        if(p==0) t^=2,t^=(1<<i  ),t>>=1;   else{
            t^=1<<p-1,t^=1<<p+1;
            t=(t&(1<<p)-1)|(t>>p)<<p-1;
        }
    }
    return t==3;
}
int cnt(int n,int t){
    int c=n; up(0,n-1,i){
        if(t&(1<<i)) --c;
    }
    return c;
}
#define pi first
#define ci second
int ans; pair<int,int> P[20]; bool made_by_joesSR=true;
int main(){
    up(0,20,i) T[1<<i]=i;
    int n=qread(),m=qread(),p=(1<<n)-1;
    up(1,m,i){
        int x=qread(),y=qread(); P[i].pi=x,P[i].ci=y;
    }
    up(0,p,i){
        up(1,m,j){
            if(!!(i&(1<<P[j].pi-1))!=P[j].ci) goto nxt;
        }
        if(cnt(n,i)%2==0&&chk(n,i)) ++ans;
        nxt:;
    }
    printf("%d\n",ans);
    return 0;
}

$\text{Subtask 1\~ 3}$，普通$\rm dp$。

#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l;i<=r;i++)
#define dn(l,r,i) for(int i=l;i>=r;i--)
using namespace std;

typedef long long LL;
const int INF =2147483647;
int qread(){
    int w=1,c,ret;
    while((c=getchar())> '9'||c< '0')
    w=(c=='-'?-1:1); ret=c-'0';
    while((c=getchar())>='0'&&c<='9')
    ret=ret*10+c-'0';
    return ret*w;
}
const int MAXC =6+3,MAXM=5e3+3;
int n,m,p=1,A[MAXC],B[MAXC];
const int MOD  =998234353;
#define dp(x,y) ((x)*3+(y))
#define pi first
#define ci second
pair<int,int> P[MAXM]; bool made_by_joesSR=true;
int main(){
    n=qread(),m=qread();
    up(1,m,i) P[i].pi=qread(),P[i].ci=qread();
    sort(P+1,P+1+m);
    if(P[1].pi==1){
        ++p;
        if(P[1].ci==0) A[dp(1,0)]=1;
        else           A[dp(0,1)]=1;
    } else A[dp(1,0)]=A[dp(0,1)]=1;
    up(2,n,i){
        bool a=true,b=true;
        if(P[p].pi==i){if(P[p].ci==0) a=false; else b=false;++p;}
        up(0,1,j) up(0,2,k){
            B[dp(j,k)]=(A[dp(j,(k+2-j)%3)]*a+A[dp(!j,k)]*b)%MOD;
        }
        memcpy(A,B,sizeof(B));
    }
    printf("%d\n",(A[dp(0,1)]+A[dp(0,2)])%MOD);
    return 0;
}

$\text{Subtask 3}$，分治。

#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l;i<=r;i++)
#define dn(l,r,i) for(int i=l;i>=r;i--)
using namespace std;

typedef long long LL;
const int INF =2147483647;
LL qread(){
    LL w=1,c,ret;
    while((c=getchar())> '9'||c< '0') w=(c=='-'?-1:1); ret=c-'0';
    while((c=getchar())>='0'&&c<='9') ret=ret*10+c-'0';
    return ret*w;
}
const int MOD=998234353;
void calc(LL n,int &a,int &b){     
    if(n==1){a=1,b=0;return;}
    LL m=n/2; int p=0,q=0; calc(m,p,q);
    q=((LL)p*q+q)%MOD,p=(LL)p*p%MOD;
    LL t=2ll*m-1; while(t<n){
        p=(LL)p*4%MOD,q=((LL)4*q+1)%MOD; ++t;
    }
    a=p,b=q;
}
LL n,m; bool made_by_joesSR=true;
int main(){
    n=qread(),m=qread();
    if(m) puts("-1"),exit(0);
    if(n%2==0){
        int a,b; calc(n/2,a,b); printf("%d\n",(a+b)%MOD);
    } else{
        int a,b; calc(n/2,a,b); printf("%d\n",(2ll*(a+b)+1)%MOD);
    }
    return 0;
}

$\text{Subtask 4}$，矩阵优化 $dp$

#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l;i<=r;i++)
#define dn(l,r,i) for(int i=l;i>=r;i--)
using namespace std;

typedef long long LL;
const int INF =2147483647;
typedef unsigned long long u64;
u64 qread(){
    u64 w=1,c,ret;
    while((c=getchar())> '9'||c< '0') w=(c=='-'?-1:1); ret=c-'0';
    while((c=getchar())>='0'&&c<='9') ret=ret*10+c-'0';
    return ret*w;
}
const int MOD =998234353;
const int MAXC=6+3,MAXN=5e3+3;
struct mtx{
    int dt[MAXC][MAXC],a,b;
    mtx(int x=0,int y=0):a(x),b(y){memset(dt,0,sizeof(dt));}
    mtx operator *(mtx t){
        int n=a,p=b,m=t.b; mtx r(n,m); up(0,p-1,i) up(0,n-1,j) up(0,m-1,k)
        r.dt[j][k]=((LL)r.dt[j][k]+(LL)dt[j][i]*t.dt[i][k])%MOD;
        return r;
    }
}o(1,6),oo(6,6);
mtx pwr(mtx x,u64 y){
    mtx r=x,t=x; --y; while(y){if(y&1) r=r*t; t=t*t,y>>=1;} return r;
}
#define pi first
#define ci second
#define dp(x,y) ((x)*3+(y))
u64 n,m,lst,T[MAXC]; bool made_by_joesSR=true; pair<u64,bool> P[MAXN];
int main(){
    up(0,1,i) up(0,2,j){
        oo.dt[dp(!i,j)][dp(i,j)]=oo.dt[dp(i,(j+2-i)%3)][dp(i,j)]=1;
    }
    n=qread(),m=qread(); up(1,m,i) P[i].pi=qread(),P[i].ci=qread();
    sort(P+1,P+1+m);
    if(P[1].pi==1){
        if(P[1].ci==0) o.dt[0][dp(1,0)]=1;
        else           o.dt[0][dp(0,1)]=1;
    } else o.dt[0][dp(1,0)]=o.dt[0][dp(0,1)]=1;
    lst=1;
    up(1,m,i){
        if(P[i].pi==1) continue;
        if(lst<P[i].pi-1) o=o*pwr(oo,(P[i].pi-1)-lst);
        memset(T,0,sizeof(T)); bool a=true,b=true;
        if(P[i].ci==0) a=false; else b=false;
        up(0,1,j) up(0,2,k){
            T[dp(j,k)]=(o.dt[0][dp(j,(k+2-j)%3)]*a+o.dt[0][dp(!j,k)]*b)%MOD;
        }
        up(0,5,j) o.dt[0][j]=T[j];
        lst=P[i].pi;
    }
    if(lst!=n) o=o*pwr(oo,n-lst);
    printf("%d\n",(o.dt[0][dp(0,1)]+o.dt[0][dp(0,2)])%MOD);
    return 0;
}