自动搬运

查看原文

来自洛谷，原作者为

	JK_LOVER 却顾所来径，苍苍横翠微。

搬运于2025-08-24 22:23:25，当前版本为作者最后更新于2020-08-04 20:39:46，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题意

使得柱状图的容量为 $X$ 。如果不存在，则输出 $-1$。否则输出任意一种方案。QAQ 。

分析

众所周知构造永远要比解决难度大，考虑这个题的特殊性

• 最左和最右的的柱子永远没法储水。

• 储水的柱子左右总有比它高的。

那么我们如果画这样一张图就一目了然了。

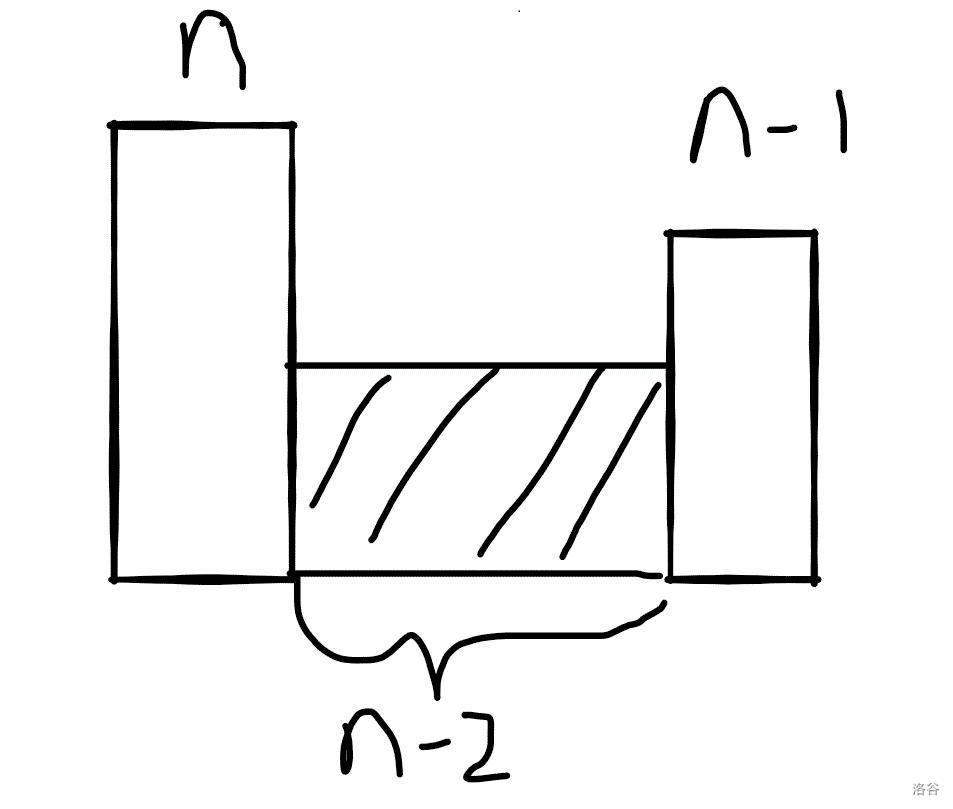
这样所有储水的柱子全在 $n$ 号和 $n-1$ 号柱子之间了。移除一个柱子的那么储水就会减少 $(n-1)-id$ 这样多。那么我们只要将标号有小到大枚举，这样就保证了不重不漏。而无解的情况就只有

$$X > (n-2)\times (n-1) - \frac{((n-2)+1)\times (n-2)}{2} $$

划重点：不要用 $dfs$ 实现这样过程，会很慢。

代码

$\text{80分的dfs}$

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1000100;
LL n,X,maxflow,d;
int ans = 0,top = 0,cnt[N],vis[N];
void dfs(LL f)
{
	if(ans) return;
	if(f == 0){
//		sort(cnt+1,cnt+1+top);
		for(int i = 1;i <= top;i++){
			printf("%d ",cnt[i]);
		}
		printf("%d ",n);
		for(int i = 1;i <= n-2;i++)
		if(!vis[i]) printf("%d ",i);
		printf("%d ",n-1);
		ans = 1;
		exit(0);
	}
	for(int i = 1;i <= n-2;i++)
	{
		if(!vis[i] && (f - ((n-1) - i) >= 0))
		{
			cnt[++top] = i;vis[i] = 1;
			dfs(f - ((n-1)-i));
		}
	}
}
int main()
{
	cin>>n>>X;
	maxflow = (n-1)*(n-2) - (1+(n-2))*(n-2)/2;
	d = maxflow - X;
	if(d < 0){
		printf("-1\n");
		return 0;
	}
	dfs(d);
	return 0;
}

$\text{100分的循环实现}$

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1000100;
LL n,X,maxflow,d;
int ans = 0,top = 0,cnt[N],vis[N];
int main()
{
	cin>>n>>X;
	maxflow = (n-1)*(n-2) - (1+(n-2))*(n-2)/2;
	d = maxflow - X;
	if(d < 0){
		printf("-1\n");
		return 0;
	}
	for(int i = 1;i <= n-2;i++)
	{
		if(d - ((n-1)-i) >= 0)
		{
			vis[i] = 1;
			cnt[++top] = i;
			d -= ((n-1)-i);
		}
	}
//	sort(cnt+1,cnt+1+top);
	for(int i = 1;i <= top;i++){
		printf("%d ",cnt[i]);
	}
	printf("%d ",n);
	for(int i = 1;i <= n-2;i++)
	if(!vis[i]) printf("%d ",i);
	printf("%d ",n-1);
	return 0;
}