自动搬运

查看原文

来自洛谷，原作者为

	panxz2009 2027 高考加油

搬运于2025-08-24 22:23:15，当前版本为作者最后更新于2024-04-16 07:39:46，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

解题思路

离线+并查集做法。

首先，如果没有删边的操作，那么这个有向图事实上只有两种可能，很简单，有环或无环。

对于无环的情况，注意到每个点出度为 $0$ 或 $1$，那么每个弹珠能到达的终止点全部相同，都是下图中的红色点。 由上图中的遍历方式，容易想到并查集的路径压缩。对于无环的情况来说，只需要将相连的两条边加入同一个并查集里即可。
对于有环的情况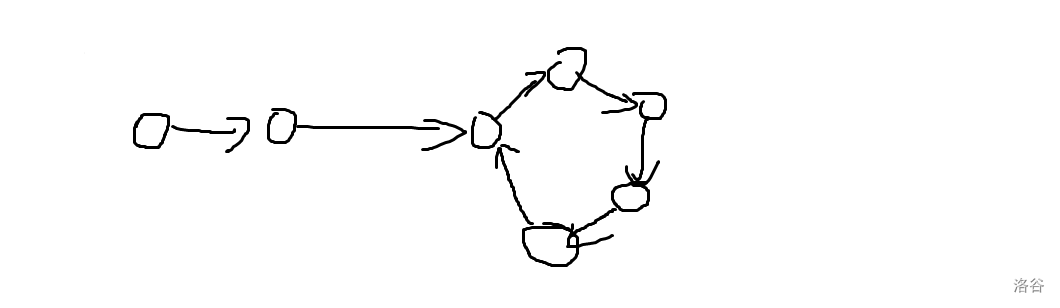， 其实与无环的情况类似，只不过在加入并查集的过程中，如果两个点已经在一个并查集中了，但还是要求合并，说明产生了环，此时只需把这个点的 fa 数组赋值为 $0$。

接下来考虑删边操作。考虑到离线，那么其实可以把询问顺序翻转，删边也就转换成了加边，那么加边的操作其实就与上述的并查集操作类似了。

代码

#include<bits/stdc++.h>
#define pb push_back
#define pii pair<int,int>
#define mkp make_pair
#define ll long long
using namespace std;
const int maxn=3e5+10;
int n,Q,to[maxn],fa[maxn],ans[maxn];
bool t[maxn];
struct ask{int op,x;}ask[maxn];
int getfa(int x)
{
	if(fa[x]==x) return x;
	return fa[x]=getfa(fa[x]);
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&to[i]);
		fa[i]=i;
	}
	scanf("%d",&Q);
	for(int i=1;i<=Q;i++)
	{
		scanf("%d%d",&ask[i].op,&ask[i].x);
		if(ask[i].op==2) t[ask[i].x]=1;
	}
	for(int i=1;i<=n;i++)
	{
		if(t[i] || !to[i]) continue;
		int fx=getfa(i),fy=getfa(to[i]);
		if(fx!=fy) fa[fx]=fy;
		else fa[fx]=0;
	}
	for(int i=Q;i>=1;i--)
	{
		if(ask[i].op==1) ans[i]=getfa(ask[i].x);
		else
		{
			if(!to[ask[i].x]) continue;
			int fx=getfa(ask[i].x),fy=getfa(to[ask[i].x]);
			if(fx!=fy) fa[fx]=fy;
			else fa[fx]=0;
		}
	}
	for(int i=1;i<=Q;i++)
	{
		if(ask[i].op==1)
		{
			if(!ans[i]) puts("CIKLUS");
			else printf("%d\n",ans[i]);
		}
	}
    return 0;
}