自动搬运

查看原文

来自洛谷，原作者为

	Fan_sheng ExplodeZero OJ现任管理员

搬运于2025-08-24 22:23:11，当前版本为作者最后更新于2023-04-02 00:19:53，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

省选两天已经考完了，出考场的时候整个人都是麻着的。这大概是我退役前最后一篇题解了，写一道有价值的黑题纪念一下吧。

性质一：一定存在一种最优的操作顺序，使得所有二操作都在一操作之前。

证明：假如先把 $a[i]$ 用一操作改成 $X$，再用二操作把所有 $X$ 改成 $Y$。显然等价于先用二操作把所有 $X$ 改成 $Y$，再把 $a[i]$ 用一操作改成 $Y$。

性质二：同一个字母不可能进行多于一次的二操作。

证明：假如已经对字母 $a$ 用了二操作，此时场上就没有 $a$ 了。如果再进行一次二操作 $a\rightarrow b$，必然先前存在 $c\rightarrow a$。不如直接 $c\rightarrow b$。

对每个字母建点。每个点对 $(u,v)$，$u$ 向 $v$ 连一条单向边。其中边权为：$s[i]=u\land t[i]\neq v$ 的位置数，如果 $u\neq v$，再加上 $c$。之后会讲这张图的含义。

原问题就可以转化：我们有 $n$ 颗棋子，第 $i$ 颗所在节点代表当前 $i$ 位置的字符，初始放在 $s[i]$ 上。如果进行 $u\rightarrow v$ 的二操作，相当于把 $u$ 上所有棋子移到 $v$ 上。然而这些移过来的棋子还需要通过一操作改成 $t[i]$，再加上二操作的代价，总代价就是 $u$ 到 $v$ 的边权。

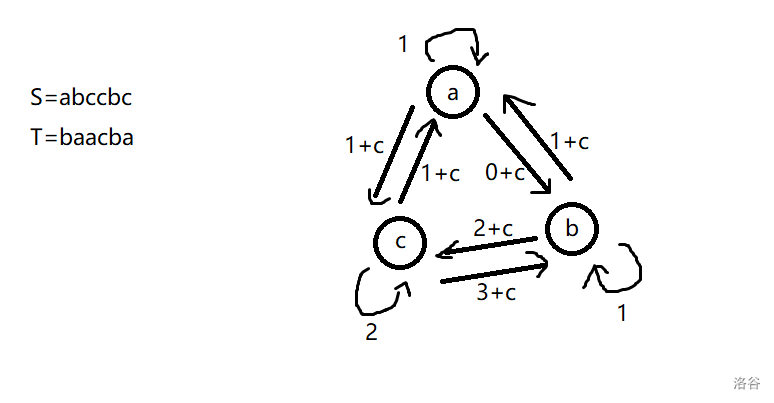
如果感觉抽象的话可以看看图。比如说 $b$ 上面有两颗棋子（分别是 $2$ 号和 $4$ 号）。我们可以用二操作把 $b$ 变成 $a$，但是 $4$ 号的终态应该是 $b$，需要再用一次一操作修改，总代价就是 $b\rightarrow a$ 的边权 $1+c$。

根据性质二，我们要为每个点都确定一条唯一的出边，形成内向基环树森林，每颗棋子都要能通过这些边到达它的终点，同时总代价最小。考虑每个点都先贪心地选最小边权出边，看看会发生什么。

• 对于一棵树（根节点自环），按反拓扑序依次挪动棋子就好了，不会产生任何冲突。

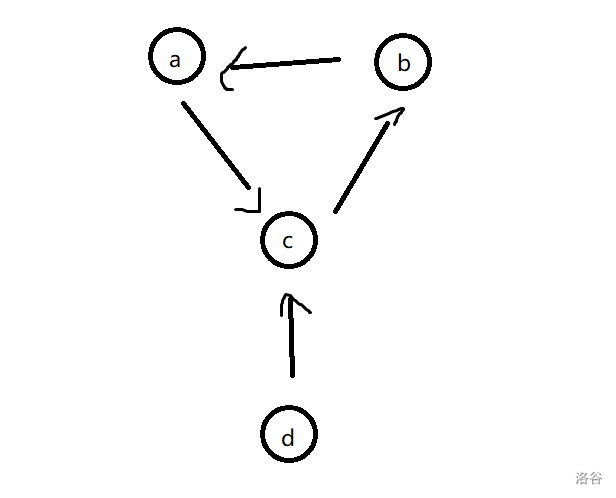
• 对于一棵基环树（如上图），只借助基环树上的边是不行了。可以考虑先把 $a$ 上的棋子通过二操作挪到 $d$ 上，这样 $a$ 节点空出来，就不会冲突了。算出来代价和原来一样。

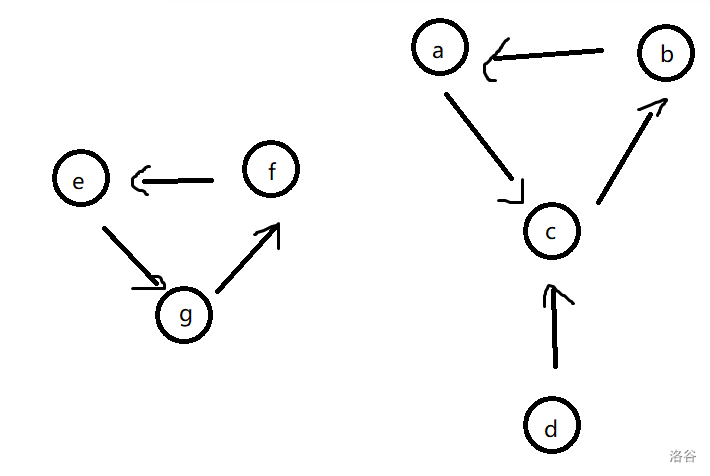
• 对于一个大小 $>1$ 的环，由于不存在叶子节点，必须借助环外的一个点来“中转”才行。如果森林中存在大小 $>1$ 的树/基环树，可以先操作完那棵树/基环树，其叶子节点会空出来。比如这张图，你可以把 $g$ 上棋子都挪到 $d$ 上，再挪到 $f$ 上，就不会冲突了。这样做的代价比原来增加了 $c$。如果图上不存在大小 $>1$ 的树/基环树，就不可能完成挪动，无解。

由于每个环都会额外贡献 $c$，我们开始的贪心策略可能不是最优的，考虑修改某些点的出边。

性质三：存在一种最优的修改策略，使得新图不会产生原图没有的环。

证明：如果出现了新环，环上一定存在一个点的出边被修改过。如果把它改回去，不仅边权会变小，同时新环也会被破开，肯定更优。

所以做法就出来了：先预处理出原图中所有的环。设 $dp[i][S][0/1]$ 表示当前要为第 $i$ 个点选择出边，$S$ 集合中的环已被破开，是否有点的出边被修改过，最小代价。

转移直接枚举出边，如果策略与原来不一样，就可以破开自己所在的环与对方所在的环。根据性质三，我们不需要考虑这么做是否会产生新的环。$0/1$ 那一维用于规避无解情况，那种情况下必须要修改策略才行。我的代码里这样会好写一点，你也可以用其他方式特判；还要注意，全是自环是一种可行的方案。

最多有 $13$ 个大小 $>1$ 的环，时间复杂度 $\mathbb O(\Sigma^2 2^{\frac{\Sigma}{2}})$。

Code

#include<bits/stdc++.h>
#define H(x) ((x)-'a'+1)
using namespace std;
typedef long long ll;
int n,c,w[27][27],nxt[27],cnt,b[27],in[27],spj=1,W[27][27];
char s[1000003],t[1000003];
ll dp[27][1<<13][2];
inline void ckmin(ll &a,ll b){a=(a<b?a:b);}
inline void toposort(){
	for(int i=1;i<=26;i++)in[nxt[i]]++;
	queue<int>q;
	for(int i=1;i<=26;i++)if(!in[i])q.emplace(i),spj=0;
	while(q.size()){
		int h=q.front();q.pop();
		if(!(--in[nxt[h]]))q.emplace(nxt[h]);
	}
	for(int i=1;i<=26;i++)if(in[i]&&nxt[i]!=i){
		++cnt;
		int now=i;
		while(in[now]){
			in[now]=0,b[now]=cnt;
			now=nxt[now];
		}
	}
	if(!cnt){
		ll ans=0;
		for(int i=1;i<=26;i++)ans+=w[i][nxt[i]];
		printf("%lld",ans),exit(0);
	}
}
inline void DP(){
	memset(dp,0x3f,sizeof(dp)),dp[0][0][0]=0;
	for(int i=1;i<=26;i++)
	for(int S=0;S<(1<<cnt);S++)
	for(int t=0;t<2;t++)
	for(int j=1;j<=26;j++){
		int T=S;
		if(b[i]&&nxt[i]!=j)T|=(1<<(b[i]-1));
		if(b[j]&&(nxt[i]!=j||b[i]!=b[j]))T|=(1<<(b[j]-1));
		ckmin(dp[i][T][t|(nxt[i]!=j)],dp[i-1][S][t]+w[i][j]);
	}
	ll ans=LLONG_MAX;
	for(int S=0;S<(1<<cnt);S++)
	for(int t=spj;t<2;t++)
	ckmin(ans,dp[26][S][t]+1ll*c*(cnt-__builtin_popcount(S)));
	printf("%lld",ans),exit(0);
}
int main(){
	scanf("%d%d%s%s",&n,&c,s+1,t+1);
	for(int i=1;i<=n;i++)W[H(s[i])][H(t[i])]++;
	for(int i=1;i<=26;i++){
		w[i][0]=0x3f3f3f3f;
		int tot=0;
		for(int j=1;j<=26;j++)tot+=W[i][j];
		for(int j=1;j<=26;j++){
			w[i][j]=tot-W[i][j];
			if(i!=j)w[i][j]+=c;
			if(w[i][j]<w[i][nxt[i]])nxt[i]=j;
		}
	}toposort(),DP();
}

我果然还是想在洛谷留下一点我的足迹。谢谢你看到这里，你们还有无限的可能，祝前程似锦。

欢迎找 bug，虽然我不太可能有精力修就是了……