自动搬运

查看原文

来自洛谷，原作者为

	Computer1828 我已看不懂我的题解，如题解有误，我也不知道如何修改了，见谅。

搬运于2025-08-24 22:22:53，当前版本为作者最后更新于2020-08-04 13:27:19，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这翻译什么鬼&一血&严重拉低AC率

题目翻译：

有 $n\cdot m$ 个点排成 $n$ 行 $m$ 列，坐标 $(i,j)$ 表示的是第 $i$ 行第 $j$ 列的点。如果两个点 $A(x_1,y_1)$ $B(x_2,y_2)$ 的距离 $\left\vert x_2-x_1 \right\vert + \left\vert y_2-y_1\right\vert = 1$ ，则 $A$ 和 $B$ 之间有边权为 $1$ 的边相连。给定整数 $k$ ，构造一个这个图的生成树，使生成树的直径恰好为 $k$ 。

首先考虑合法的 $k$ 的范围是多少。

不难发现，当 $n$ 为奇数时， $k\in [n+m-2,nm-1]$ ；当 $n$ 为偶数时， $k\in [n+m-1,nm-1]$ 。这里分类讨论特判一下即可。

然后考虑怎么构造一个直径长度为 $k$ 的生成树。可以分类讨论一下。

以下的图中每个格子代表一个点，左上角的格子的坐标是 $(1,1)$ ，右下角的格子的坐标是 $(n,m)$ ，相邻的格子之间有一条边权为 $1$ 的边，红色粗线表示的是生成树的边。

当 $n$ 为奇数时，可以先构造出 $k = n+m-2$ 的情况：

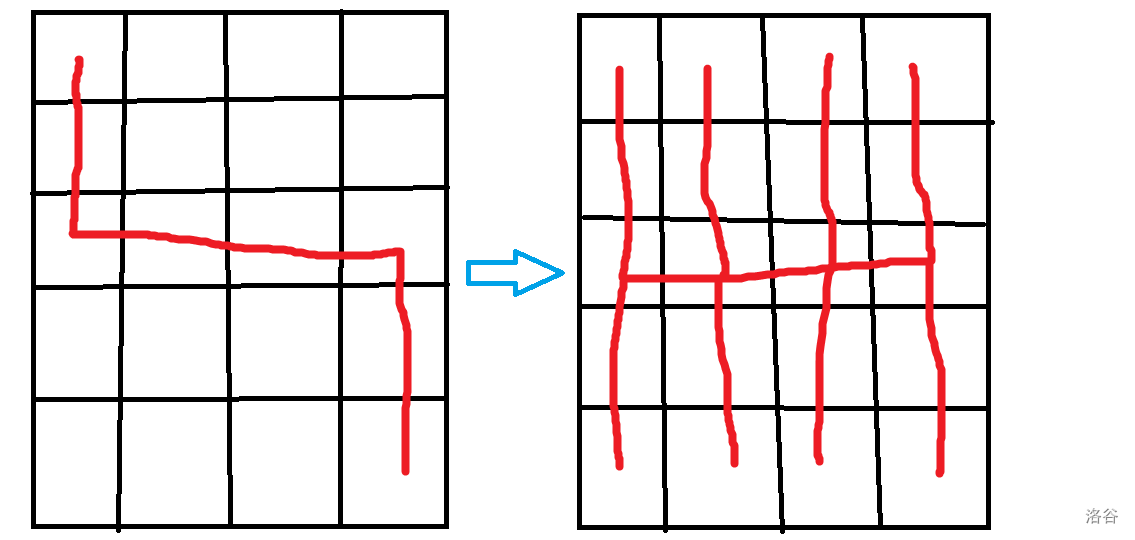
然后构造出 $k = nm-1$ 的情况：

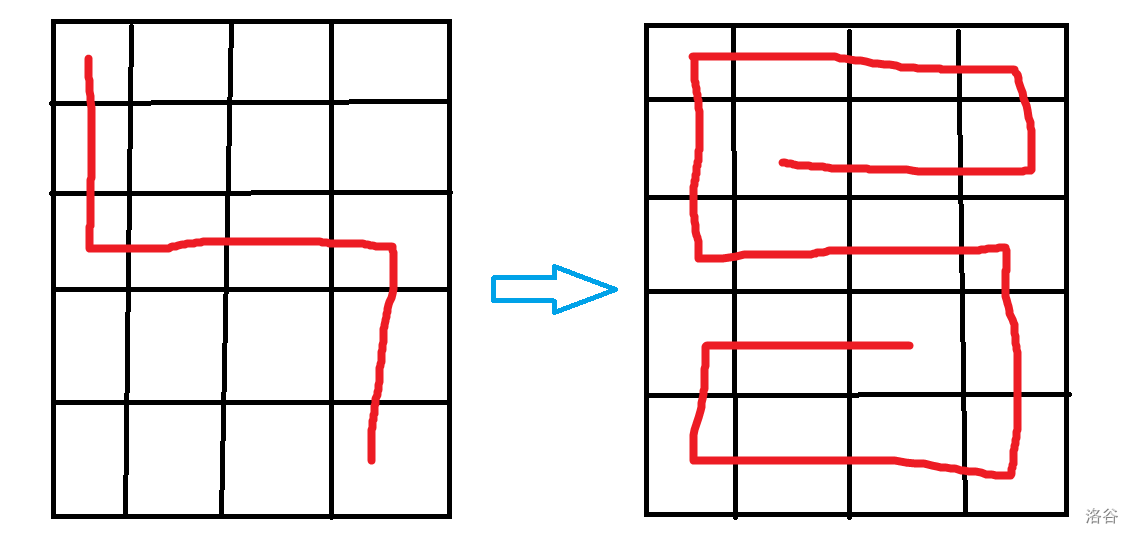
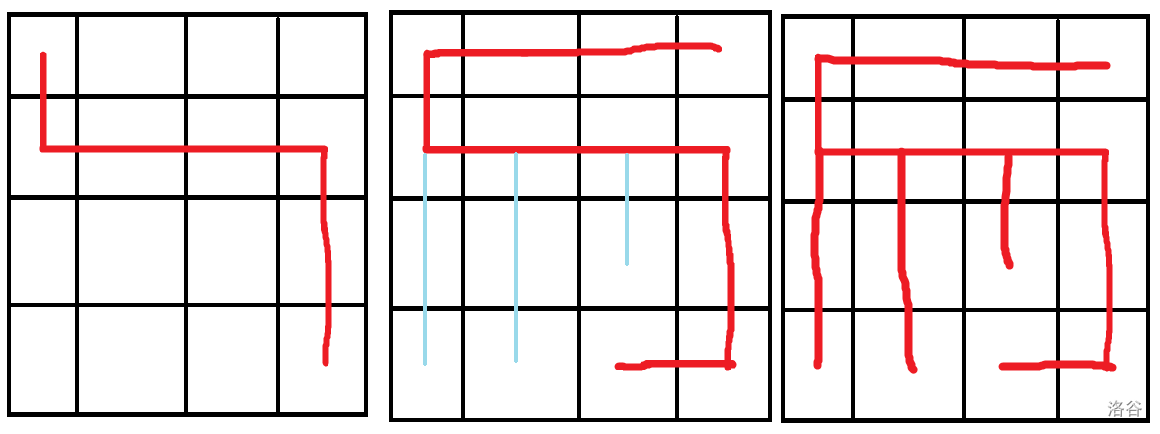
思考一下是如何从左边构造出右边的（以下是 $n = 5,m = 4,k = 9$ 的情况）：

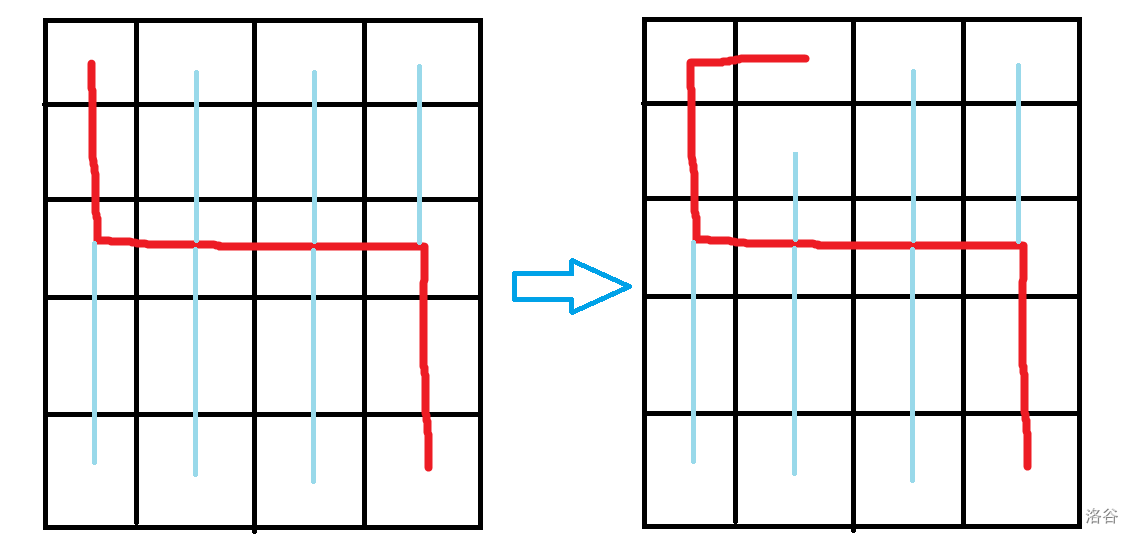
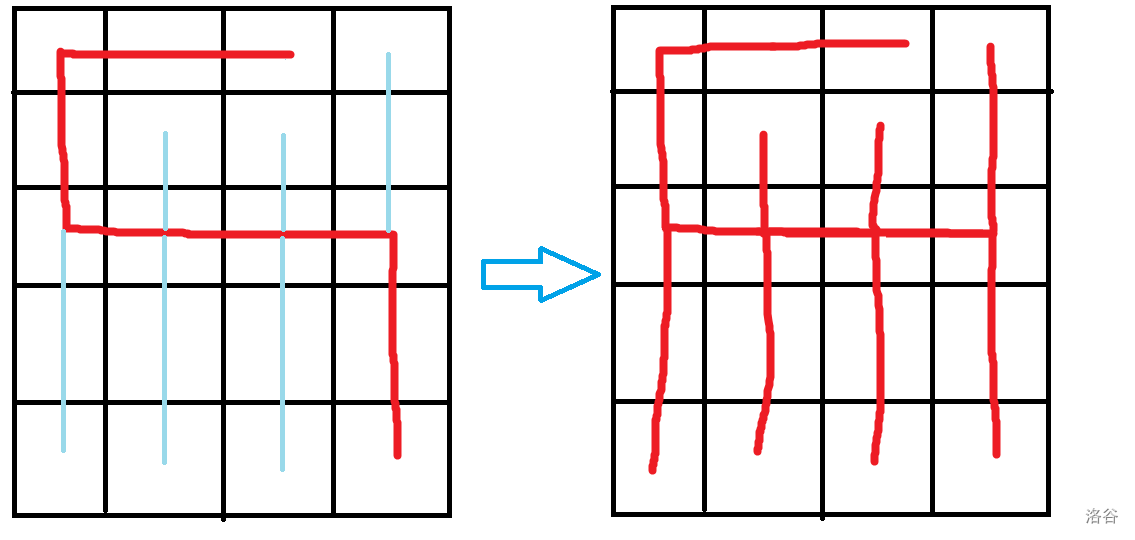
也就是说，先构造出一条主干 A ，然后以主干的端点为起点，继续构造（假设后来构造的叫主干 B ），直到主干 A 的长度加上主干 B 的长度 $= k$ 为止。对于其它不在主干 A 或主干 B 上的点，沿竖直方向连接到主干 A 上。

当 $n$ 为偶数时，仿照上面的做法就行了（以下是 $n = 4,m = 4,k = 10$ 的情况）:

代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,k;
bool flag;
int f[1005][1005];
inline void add(int x1,int y1,int x2,int y2){
	if(flag) swap(x1,y1),swap(x2,y2);
	printf("%d %d %d %d\n",x1,y1,x2,y2);
}
inline void dosth1(){
	if(k<n+m-2 || k>=n*m){
		printf("NIE\n");
		return ;
	} 
	printf("TAK\n");
	k -= n+m-2;
	for(int i = 1;i<=n/2;++i) add(i,1,i+1,1);
	for(int i = 1;i<m;++i) add(n/2+1,i,n/2+1,i+1);
	for(int i = 1;i<=n/2;++i) add(i+n/2+1,m,i+n/2,m);
	for(int i = 1;i<=n/2;++i) for(int j = 2;j<=m;++j) f[i][j] = 1;
	for(int i = 1;i<=n/2;++i) for(int j = 1;j<m;++j) f[i+n/2+1][j] = -1;
	for(int i = 1;i<=n/2 && k;++i){
		if(i%2 == 1){
			for(int j = 2;j<=m && k;++j){
				if(j == 2){
					if(i == 1) add(i,j,i,j-1);
					else add(i,j,i-1,j);
				}else add(i,j,i,j-1);
				f[i][j] = 0,k--;
			}
		}else{
			for(int j = m;j>=2 && k;--j){
				if(j == m) add(i,j,i-1,j);
				else add(i,j,i,j+1);
				f[i][j] = 0,k--;
			}
		}
	}
	for(int i = n;i>n/2+1 && k;--i){
		if(i%2 == 1){
			for(int j = m-1;j>=1 && k;--j){
				if(j == m-1){
					if(i == n) add(i,j,i,j+1);
					else add(i,j,i+1,j);
				}else add(i,j,i,j+1);
				f[i][j] = 0,k--;
			}
		}else{
			for(int j = 1;j<m && k;++j){
				if(j == 1) add(i,j,i+1,j);
				else add(i,j,i,j-1);
				f[i][j] = 0,k--;
			}
		}
	}
	for(int i = 1;i<=n;++i) for(int j = 1;j<=m;++j) if(f[i][j]) add(i,j,i+f[i][j],j);
}

inline void dosth2(){
	if(n == 2) swap(n,m),flag = true;
	if(k<n+m-1 || k>=n*m){
		printf("NIE\n");
		return ;
	} 
	printf("TAK\n");
	k -= n+m-2;
	for(int i = 1;i<n/2;++i) add(i,1,i+1,1);
	for(int i = 1;i<m;++i) add(n/2,i,n/2,i+1);
	for(int i = 1;i<=n/2;++i) add(i+n/2-1,m,i+n/2,m);
	for(int i = 1;i<n/2;++i) for(int j = 2;j<=m;++j) f[i][j] = 1;
	for(int i = 1;i<=n/2;++i) for(int j = 1;j<m;++j) f[i+n/2][j] = -1;
	for(int i = 1;i<n/2 && k;++i){
		if(i%2 == 1){
			for(int j = 2;j<=m && k;++j){
				if(j == 2){
					if(i == 1) add(i,j,i,j-1);
					else add(i,j,i-1,j);
				}else add(i,j,i,j-1);
				f[i][j] = 0,k--;
			}
		}else{
			for(int j = m;j>=2 && k;--j){
				if(j == m) add(i,j,i-1,j);
				else add(i,j,i,j+1);
				f[i][j] = 0,k--;
			}
		}
	}
	for(int i = n;i>n/2 && k;--i){
		if(i%2 == 1){
			for(int j = 1;j<m && k;++j){
				if(j == 1) add(i,j,i+1,j);
				else add(i,j,i,j-1);
				f[i][j] = 0,k--;
			} 
		}else{
			for(int j = m-1;j>=1 && k;--j){
				if(j == m-1){
					if(i == n) add(i,j,i,j+1);
					else add(i,j,i+1,j);
				}else add(i,j,i,j+1);
				f[i][j] = 0,k--;
			}
		}
	}
	for(int i = 1;i<=n;++i) for(int j = 1;j<=m;++j) if(f[i][j]) add(i,j,i+f[i][j],j);
}
int main(){
	scanf("%d%d%d",&n,&m,&k);
	if(m%2 == 1) swap(n,m),flag = true;
	if(n%2 == 1) dosth1();
	else dosth2();
	return 0;
}

其实代码可以写得更短，并不需要冗杂的分类讨论，但是不分类讨论的写法的细节过于复杂，不便在此赘述。