自动搬运

查看原文

来自洛谷，原作者为

	王鲲鹏 亦余心之所善兮，虽九死其犹未悔。

搬运于2025-08-24 22:22:50，当前版本为作者最后更新于2020-09-25 10:47:12，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

LGV 引理（Lindstrom-Gessel-Viennot lemma）

本文主要分为对 引理的阐述与证明 和 这道题的解法。然鹅OIer 不需要证明。

LGV 引理 内容

• $G$ 是一个有限的带权有向无环图。每个顶点的度是有限的，不存在有向环（所以路径数量是有限的）。
• 起点 $A=\{a_1,\cdots,a_n\}$，终点 $B=\{b_1,\cdots,b_n\}$。
• 每条边 $e$ 有权 $w_e$，并假定值属于某 交换环 。
• 对于一个有向路径 $P$，定义 $\omega(P)$ 为路径上所有边权的积。
• 对任意顶点 $a$，$b$，定义 $e(a,b)=\sum\limits_{P:a \to b}{\omega(P)}$。

设矩阵

$$M= \begin{pmatrix} e(a_1,b_1) & e(a_1,b_2) & \cdots & e(a_1,b_n) \\ e(a_2,b_1) & e(a_2,b_2) & \cdots & e(a_2,b_n) \\ \vdots & \vdots & \ddots & \vdots \\ e(a_n,b_1) & e(a_n,b_2) & \cdots & e(a_n,b_n) \\ \end{pmatrix} $$

从 $A$ 到 $B$ 的不相交路径 $P=(P_1,P_2,\cdots,P_n)$，$P_i$ 表示从 $a_i$ 到 $b_{\sigma(i)}$ 的一条路径，其中 $\sigma$ 是一个排列（置换），并且满足对任意 $i\not=j$，$P_i$ 与 $P_j$ 没有公共点。记 $\sigma(P)$ 表示 $P$ 对应的排列。

引理说明，$M$ 的行列式是所有从 $A$ 到 $B$ 的不相交路径 $P=(P_1,\cdots,P_n)$ 的带符号和。其中符号指 $\sigma(P)$ 的逆序数的奇偶性： $(-1)^{\text{逆序数}}$，记为 $\mathrm{sign}(\sigma(P))$。

$$\mathrm{det}(M)=\sum_{P:A\to B}{\mathrm{sign}(\sigma(P))\prod_{i=1}^{n}\omega(P_i)} $$

证明

对一组路径 $P$，若对任意 $i\not=j$，$P_i$ 与 $P_j$ 无公共点，则称 $P$ 是一组不相交路径，否则为一组相交路径。为了简便，在下面相交路径记作 $P^c$，不相交路径记作 $P^u$。不做特殊说明时，$P$ 为一组平凡的路径。当带下标时，指一条路径。定义 $\omega(P)=\omega(P_1)\omega(P_2)\cdots\omega(P_n)$。

根据定义，

$$\begin{aligned} \mathrm{det}(M) &=\sum_{\sigma \in S_n}\mathrm{sign}(\sigma)\prod_{i=1}^{n}e(a_i,b_{\sigma(i)}) \\ &=\sum_{\sigma \in S_n}\mathrm{sign}(\sigma)\prod_{i=1}^{n}\sum_{P_i:a_i \to b_{\sigma(i)}}\omega(P_i) \end{aligned} $$

$\prod_{i=1}^{n}\sum_{P_i:a_i \to b_{\sigma(i)}}\omega(P_i)$ 展开后对应所有排列为 $\sigma$ 的路径组 $P$ ，

$$\begin{aligned} \mathrm{det}(M) &=\sum_{\sigma \in S_n}\mathrm{sign}(\sigma)\sum_{P}\omega(P),P:(a_1,\cdots,a_n)\to(b_{\sigma(1)},\cdots,b_{\sigma(n)}) \\ &= \sum_{P:A \to B}\mathrm{sign}(\sigma(P))\omega(P) \end{aligned} $$

现在等式的形式已与定理相像，但是 $P$ 的含义不同。

$$\mathrm{det}(M)= \sum_{P^u:A \to B}\mathrm{sign}(\sigma(P^u))\omega(P^u)+\sum_{P^c:A \to B}\mathrm{sign}(\sigma(P^c))\omega(P^c) $$

故若引理成立，必有 $\sum_{P^c:A \to B}\mathrm{sign}(\sigma(P^c))\omega(P^c)=0$ 。

设 $C$ 为所有 $P^c$ 构成的集合。如果我们能构造一个双射关系 $f:C \to C$，满足对任意 $P^c\in C$， $\omega(f(P^c))=\omega(P^c)$，$\mathrm{sign}(\sigma(f(P^c)))=-\mathrm{sign}(\sigma(P^c))$，根据重排列定理，

$$\sum_{P^c}\mathrm{sign}(\sigma(P^c))\omega(P^c) =\sum_{P^c}\mathrm{sign}(\sigma(f(P^c)))\omega(f(P^c)) $$$$\begin{aligned} \sum_{P^c}\mathrm{sign}(\sigma(P^c))\omega(P^c) &= \frac{1}{2}\sum_{P^c}\mathrm{sign}(\sigma(P^c))\omega(P^c)+\frac{1}{2}\sum_{P^c}\mathrm{sign}(\sigma(f(P^c)))\omega(f(P^c)) \\ &= \frac{1}{2}\sum_{P^c}\mathrm{sign}(\sigma(P^c))\omega(P^c)+\frac{1}{2}\sum_{P^c}-\mathrm{sign}(\sigma(P^c))\omega(P^c) \\ &= 0 \end{aligned} $$

确实可以构造：

考虑 $P=(P_1,P_2,\cdots,P_n)$，$P \in C$，中找到最小的二元组 $(i,j)$ 满足 $P_i$ 和 $P_j$ 有交，将相交之后的路径交换一下，交换后得到 $P'$ 。显然有 $P' \in C$，$P' \not= P$。

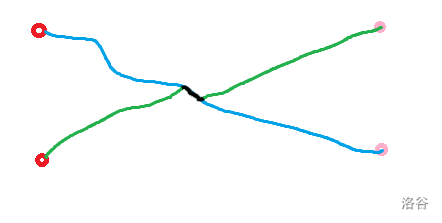
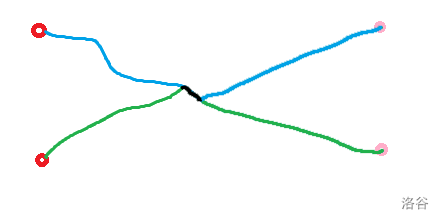
这里就不写式子了 可以直观理解一下 就是因为懒，因为边还是那些边，边权属于交换环，所以 $\omega(P)$ 不变。另一个影响是交换了两条路径的终止节点，即交换了排列中的两个元素，根据我们学前班就学过的线性代数，逆序对数的奇偶改变，所以 $\mathrm{sign}(\sigma(P'))=-\mathrm{sign}(\sigma(P))$。

最后我们还可以注意到，对于 $P'$，最小的二元组还应该是 $(i,j)$，那么 $f(P')=P$。籍此可证 $f$ 是双射。

证毕。

完结撒花lalala

差点忘了这道题还没有说...

LuoguP6657 模板

好像比定理削了好多东西...

因为这是在方格图上，因为坐标是单调的，当 $\sigma \not=(1,2,\cdots,n)$ 时，显然不存在不相交路径。

$$\text{右式}=\sum_{P:(P_i:a_i\to b_i)}1$$

即为所求。

那么构造矩阵，$e(a_i,b_j)=\binom{b_j-a_i+n-1}{n-1}$。高斯消元求行列式即可。

参考资料

1. 维基百科 挺详细的就是没中文...
2. OI Wiki.

真·完结撒花~~~

---

update 2021-05-27 感谢 @oisdoaiu 的指正