自动搬运

查看原文

来自洛谷，原作者为

	有趣的问题 心有无羁鸿鹄志，思存一举大鹏鸣

搬运于2025-08-24 22:22:45，当前版本为作者最后更新于2022-11-09 22:41:40，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

提供一种不用倒三角形也不用单调队列的做法。

题意

给定一个等边三角形的数字阵，求所有边长为给定值的子三角形的最大值之和。

思路

看到这题，很容易想到用一个类似 ST 表的东西来做。对于每个点，我们维护以该点为三角形上顶点的子三角形的最大值。参考 ST 表的做法，我们只用维护边长为 $2$ 的次方的子三角形，然后用某种方法拼出查询所需要的三角形就可以了。

怎么拼呢？设查询的三角形边长为 $h$，也就是题目中输入的 $k$，那么显然我们需要用边长为 $2^{\log_2 k}$ 的三角形来拼它。首先需要下图中的三个：

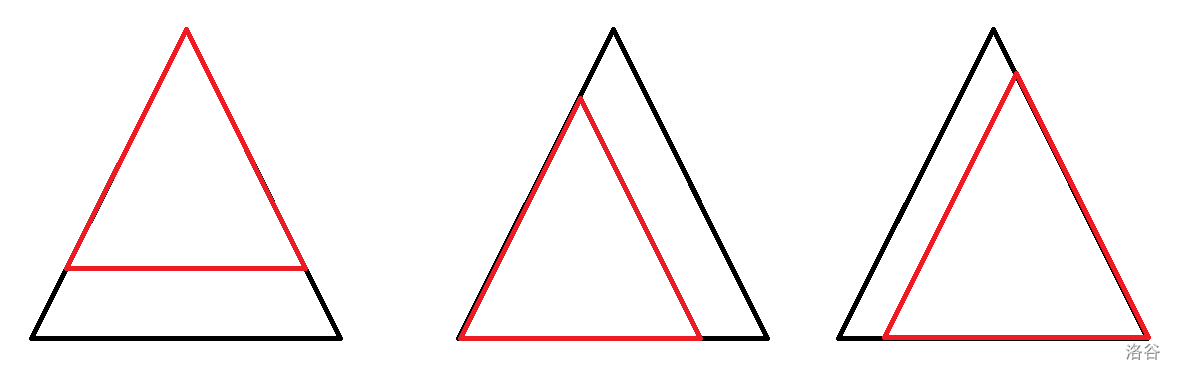
然后我们发现一个严重的问题：中间可能会有一个小三角形没有被覆盖到！

于是我们可以在底部正中间再放一个同样大小的三角形：

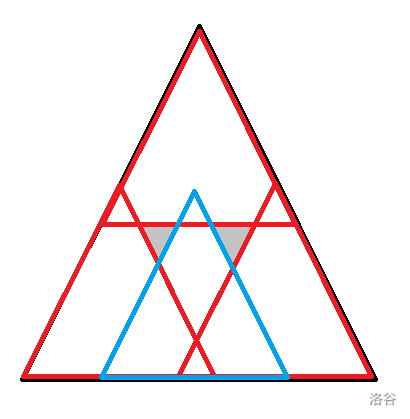
可是问题并没有完全解决，图中灰色的两块仍然没有被覆盖到啊……

于是我们发扬人类智慧：放一个不行，就放三个！

就有了下面这个：

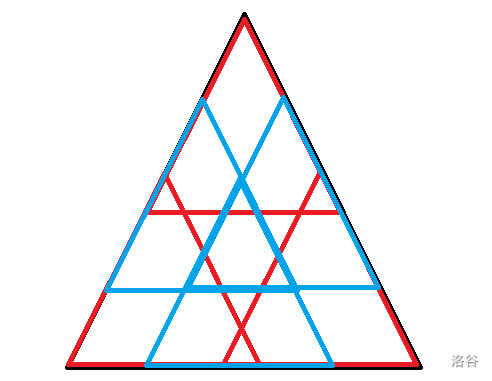
容易证明，这样一定可以把中间的部分覆盖完（考虑红色三角形边长恰好是大三角形边长一半的情况）。

实现细节

想到这些，我兴致勃勃的写完交了一发：MLE。然后发现被毒瘤出题人卡空间了。注意到这题的询问子三角形大小是固定的，因此我们的 ST 表可以滚动起来，保留 $\log_2 k$ 的值就可以了。另外位运算什么的细节也比较多，比较考验仔细程度。

丑陋的代码

#include <bits/stdc++.h>
using namespace std;
int n,h,val[3005][3005],st[3005][3005][2],lg[3005],k;
long long ans;
int query(int x,int y){
	int l=x+h-1,r=y+h-1; 
	int u=k&1;
	int ans=max(st[x][y][u],max(st[l-(1<<k)+1][y][u],st[l-(1<<k)+1][r-(1<<k)+1][u]));
	if(k<=1)return ans;
	int cha=(h-(1<<k))>>1;
	ans=max(max(ans,st[l-(1<<k)+1][y+cha][u]),max(st[x+cha][y][u],st[x+cha][y+cha][u]));
	return ans; 
}
signed main(){
    freopen("star.in","r",stdin);
    freopen("star.out","w",stdout);
	cin>>n>>h;
	k=log2(h);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			scanf("%d",&val[i][j]);
			st[i][j][0]=val[i][j];
		}
	}
	for(int t=1;t<=k;t++){
		int u=t&1,v=u^1;
		for(int i=1;i+(1<<t)-1<=n;i++){
			for(int j=1;j<=i;j++){
				st[i][j][u]=max(max(st[i][j][v],st[i+(1<<t-1)][j][v]),st[i+(1<<t-1)][j+(1<<t-1)][v]);
				if(t>1){
					st[i][j][u]=max(max(st[i][j][u],st[i+(1<<t-1)][j+(1<<t-2)][v]),max(st[i+(1<<t-2)][j][v],st[i+(1<<t-2)][j+(1<<t-2)][v]));
				}
			}
		}
	}
	for(int i=1;i<=n-h+1;i++){
		for(int j=1;j<=i;j++){
			ans+=query(i,j);
		}
	}
	cout<<ans;
	return 0;
}