自动搬运

查看原文

来自洛谷，原作者为

	chen_qian 退谷了家人们

搬运于2025-08-24 22:22:44，当前版本为作者最后更新于2022-08-12 12:03:32，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

以下做法来自大佬Daniel13265，复杂度为线性。

考虑暴力的 $\text{dp}$。定义 $f_{i,j}$ 表示前 $i$ 个分成 $j$ 段的答案。方程如下。复杂度 $O(n^2)$

$$f_{i,j}=\max\limits_{l=i-k}^{i-1}(f_{l,j-1}+\max\limits_{r=l+1}^{i}(a_r)) $$

考虑如何优化这个 $\text{dp}$，显然枚举过程已经是最优，只能从状态上简化。可以发现这样一个事实，我们之前枚举的大部分状态对于最终的答案都是没有贡献的。借此，我们发现对于 $i$，只有 $f_{i,\left \lceil \frac{i}{k} \right \rceil }$ 对之后的答案有贡献。证明如下

• 若 $j<\left \lceil \frac{i}{k} \right \rceil$，那么必定有一段长度大于 $k$。

• 若 $j>\left \lceil \frac{i}{k} \right \rceil$，由上分析可知后面最少也要 $\left \lceil \frac{n-i}{k} \right \rceil$ 段，所以有 $j+\left \lceil \frac{n-i}{k} \right \rceil >\left \lceil \frac{i}{k} \right \rceil + \left \lceil \frac{n-i}{k} \right \rceil \geqslant \left \lceil \frac{n}{k} \right \rceil$ 一定不满足。

所以记 $g_i=f_{i,\left \lceil \frac{i}{k} \right \rceil }$。根据如上的方程，能够向 $g_i$ 贡献的只有满足 $i-k\leqslant j \leqslant i-1$ 且 $\left \lceil \frac{i}{k} \right \rceil-1=\left \lceil \frac{j}{k} \right \rceil$ 的 $j$。所以方程为：

$$g_{i}=\max _{j=i-k}^{k \times\left\lfloor\frac{i-1}{k}\right\rfloor}\left(g_{j}+\max _{k=j+1}^{i} a_{k}\right) $$

做到这里，就可以用单调栈+线段树做到 $O(n\log n)$。已经可以解决这个问题，也是大部分题解所用到的。

接下来就是如何优化到线性。

根据上面的 $\text{dp}$ 我们发现，序列实际上是被分割成 $\left \lceil \frac{n}{k} \right \rceil$，每段为 $k$ 长度。每一段只能对下一段贡献答案。那么我们可以通过对于每一段进行预处理，同时修改同一块中的枚举顺序来加速回答问题。如下图。

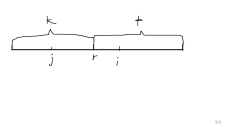
$r$ 为块的分界点我们从块的右端点倒序枚举需要更新的 $i$。显然左端点 $j$ 也在更新。如果我们假设 $s(l,r)$ 是区间 $[l,r]$ 的最大值，对于处于 $[j,r]$ 之间 $k$ 其产生的贡献是 $\max(g_k+s(k+1,r),g_k+s(r,i))$，对于后面的一部分 $s(r,i)$ 只与 $i$ 有关，只需要维护前一个块中的后缀最大值即可，对于前面一部分只与 $k$ 有关，同样可以在移动 $i$ 的过程中维护。做到 $O(1)$ 转移。复杂度为 $O(n)$。

#include<bits/stdc++.h>
#define N 1000005
#define ll long long
using namespace std;
int n,m,a[N];
ll f[N],maxn[N];
int x[N];
int pos[N],L[N],R[N],numb;
int main(){
   scanf("%d%d",&n,&m);
   for(int i=1;i<=n;i++) scanf("%d",&a[i]);
   numb=n/m;
   for(int i=1;i<=numb;i++){
   	L[i]=R[i-1]+1;
   	R[i]=i*m;
   }
   if(R[numb]<=n) numb++,L[numb]=R[numb-1]+1,R[numb]=n;
   for(int i=1;i<=numb;i++){
   	for(int j=L[i];j<=R[i];j++){
   		if(j==L[i]) x[j]=a[j];
   		else x[j]=max(x[j-1],a[j]);
   	}	
   }
   for(int i=L[1];i<=R[1];i++) f[i]=x[i];
   for(int i=R[1];i>=L[1];i--) maxn[i]=max(maxn[i+1],f[i]);
   for(int k=2;k<=numb;k++){
   	ll mx=0;
   	int j=R[k-1],mx2=0;
   	while(j>R[k]-m){
   		mx=max(mx,f[j]+mx2);
   		mx2=max(mx2,a[j]);
   		j--;
   	}
   	for(int i=R[k];i>=L[k];i--){
   		mx=max(mx,f[j]+mx2);
   		f[i]=max(mx,maxn[j]+x[i]);
   		mx2=max(mx2,a[j]);
   		maxn[i]=max(maxn[i+1],f[i]);
   		j--;
   	}
   	
   }
   cout<<f[n]<<endl;
   return 0;
}