自动搬运

查看原文

来自洛谷，原作者为

	command_block 众水皆昂首，饮月唯我一。

搬运于2025-08-24 22:22:43，当前版本为作者最后更新于2021-07-14 16:03:56，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题意 ： 商店里有 $n$ 个物品，每个物品有种类与价格。

对于第 $i$ 个种类，需要购买商品的个数在 $[l_i,r_i]$ 之间。

求出前 $k$ 便宜的方案的价钱，或指出不存在。

$n,m,k\leq 2\times 10^5$ ，时限$\texttt{2s}$。

---

• Part0

先介绍解决这类“前 $k$ 优”问题的一个通用思路。

我们考虑方案与方案之间的转移。

对于方案 $S$ ，记 ${\rm trans}(S)$ 为 $S$ 的后继方案集合（具体定义暂不明确）。

我们按以下流程求解问题。

• 将花费最小的方案加入小根堆中

• 重复执行直到堆为空，或已得到所有答案

  • 将堆顶方案 $S$ 输出并弹出

  • 将 ${\rm trans}(S)$ 中的各个方案加入堆中

考虑怎样设计 ${\rm trans}(S)$ 才能使得这个算法正确。

将 $S$ 向 ${\rm trans}(S)$ 连边，形成一张有向图。

• 所有方案形成一棵以花费最小的方案为根的外向树。

  这保证了不重不漏。

• ${\rm trans}(S)$ 的权值都大于等于 $S$ 的权值。

这样，不难证明前 $k$ 优的方案构成一个包含根的联通块。我们前述的算法可以找出这个联通块。

• Part1 : $m=1,l=r$

将物品按照价格从小到大排序，花费最小的方案是选择最左的 $l$ 个物品。

我们按如下的方法构造 $\rm trans$ ：

• 将最左的能右移的物品右移若干，但不能跨越其他已选的物品。

不难发现，这样调整之后权值必然变大，且得到所有方案的方法数恰都为 $1$。符合我们的要求。

如图是一个方案对应的调整方法。

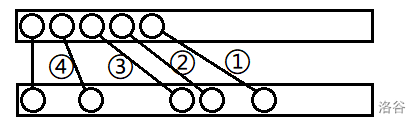
观察 ： 在任意时刻，一定是前面有一个前缀是紧密连续的，然后将这个前缀的末端向右移若干。

美中不足的是，单个 $\rm trans(S)$ 集合的大小可能达到 $O(n)$ ，不能保证复杂度。

我们改而让物品每次只能右移一位，并加入当前物品的概念，将 $\rm trans$ 改为 ：

• 将当前物品改为紧密前缀的末端（最靠左的能右移的物品）。

• 将当前物品右移一位。

不难发现这两种 $\rm trans$ 是等价的。“当前物品的连续移动”对应前文“将最左的能右移的物品右移若干”。

形式化地，记 $(x,y,z)$ 表示前缀 $[1,x]$ 还没有动，当前物品位于 $y$ ，当前物品右侧的物品位于 $z$ 的方案。

转移 ： $(x,y,z)\rightarrow (x,y+1,z)$ 或 $(x-1,x+1,y-1)$。分别对应“移一步”与“ ‘当前物品’前移然后移一步”。

• Part1.5 : $m=1$

只需要稍作修正，对于初始未移动的前缀 $(y-1,y,+\infty)$ ，钦定其可以转移到 $(y,y+1,+\infty)$ （多选一个）即可。

• Part2 : $m>1,l_i=r_i=1$

最优方案是每个种类选择最小的。

按如下的方法构造 $\rm trans$ ：

从前往后考虑种类，记当前种类为 $p$。

• 将种类 $p$ 所选的数右移一位。

• 将 $p$ 后移若干，再将种类 $p$ 所选的数右移一位。

可惜，单个 $\rm trans(S)$ 集合的大小不能保证。

原先的 $\rm trans(S)$ 的结构形如图上半部。

我们将儿子的权值从小到大排序，然后将儿子串起来（如图下半部），即可将度数变小。

在本题中，我们将种类按照 最小值与次小值的差 从小到大排序，然后如此构造 $\rm trans$ ：

• 将种类 $p$ 所选的数右移一位。

• 将 $p$ 后移一位，再将种类 $p$ 所选的数右移一位。

• 若 $p$ 所在种类目前选择次小值，则恢复为最小值。然后将 $p$ 后移一位，再将种类 $p$ 所选的数右移一位。

  （我们的排序能保证这一步权值不降）

  这一步具体的情形如下图 ：

  

• Part3 : 一般情况

考虑 Part1.5 中的算法，其实就是将 $m=1$ 的问题变成了一个黑箱，支持 $O(\log n)$ 得到下一个最优的解。

观察 Part2 中的算法，其实就是维护 $m$ 个黑箱（排好序的数组），操作中只需要访问黑箱的下一个解。

将这两个算法配合起来即可 $O(n\log n)$ 解决本题。

#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#define ll long long
#define pb push_back
#define MaxN 200500
using namespace std;
const ll INF=1ll<<60;
struct Data{
  int x,y,z;ll sum;
  bool operator < (const Data &A) const
  {return sum>A.sum;}
};
struct SeqDS
{
  vector<ll> ans;
  vector<int> a;
  priority_queue<Data> q;
  int l,r;
  void calc(int p)
  {
    if (p<ans.size())return ;
    if (q.empty()){ans.pb(INF);return ;}
    Data now=q.top();q.pop();
    int x=now.x,y=now.y,z=now.z;ll sum=now.sum;
    ans.pb(sum);
    if (z==a.size()-1&&x+1==y&&y+1<r)q.push((Data){x+1,y+1,z,sum+a[y+1]});
    if (y>=0&&y+1<=z)q.push((Data){x,y+1,z,sum-a[y]+a[y+1]});
    if (x>=0&&x+1<y)q.push((Data){x-1,x+1,y-1,sum-a[x]+a[x+1]});
  }
  void Init()
  {
    sort(a.begin(),a.end());
    if (l>a.size()){ans.pb(INF);ans.pb(INF);return ;}
    r=min(r,(int)a.size());
    ll sum0=0;
    for (int i=0;i<l;i++)sum0+=a[i];
    q.push((Data){l-2,l-1,a.size()-1,sum0});
    calc(0);calc(1);
  }
}T[MaxN];
struct Data2{
  int p,j;ll sum;
  bool operator < (const Data2 &A) const
  {return sum>A.sum;}
};
int tp[MaxN];
bool cmp(int A,int B)
{return T[A].ans[1]-T[A].ans[0]<T[B].ans[1]-T[B].ans[0];}
priority_queue<Data2> q;
int n,m,k;
int main()
{
  scanf("%d%d%d",&n,&m,&k);
  for (int i=1,c,x;i<=n;i++){
    scanf("%d%d",&c,&x);
    T[c].a.pb(x);
  }
  ll sum0=0;
  for (int i=1;i<=m;i++){
    scanf("%d%d",&T[i].l,&T[i].r);
    T[i].Init();tp[i]=i;
    sum0=min(INF,sum0+T[i].ans[0]);
  }
  sort(tp+1,tp+m+1,cmp);
  int cnt=0;
  q.push((Data2){0,0,sum0});
  while(cnt<k&&!q.empty()){
    Data2 now=q.top();q.pop();
    int p=now.p,j=now.j;ll sum=now.sum;
    if (sum>=INF)break;
    printf("%lld\n",sum);cnt++;
    if (p<m&&j==1)
      q.push((Data2){p+1,1,sum-T[tp[p]].ans[1]+T[tp[p]].ans[0]-T[tp[p+1]].ans[0]+T[tp[p+1]].ans[1]});
    if (p<m)
      q.push((Data2){p+1,1,sum-T[tp[p+1]].ans[0]+T[tp[p+1]].ans[1]});
    if (p>=1){
      T[tp[p]].calc(j+1);
      q.push((Data2){p,j+1,sum-T[tp[p]].ans[j]+T[tp[p]].ans[j+1]});
    }  
  }for (int i=cnt+1;i<=k;i++)puts("-1");
  return 0;
}