自动搬运

查看原文

来自洛谷，原作者为

	dengyaotriangle 我弱弱 您强强 嘤嘤嘤

搬运于2025-08-24 22:22:31，当前版本为作者最后更新于2020-06-24 17:07:43，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

首先，我们要求的是一个子树和状物体，那么就可以先考虑一个点，对于它的所有祖先的答案的贡献。

首先考察 $c,c+1,c+2,\cdots$ 的二进制表示。

随便选一个 $c$，就比如说 $c=3$：

那么 $c,c+1,c+2,\cdots$ 的二进制表示就是：

$$\begin{matrix}+0&=&0011\\+1&=&0100\\+2&=&0101\\+3&=&0110\\+4&=&0111\\+5&=&1000\\+6&=&1001\\+7&=&1010\\+8&=&1011\\+9&=&1100\\\cdots&\cdots&\cdots\end{matrix} $$

我们随便找一位来看，比如说第二低的位：

$$\begin{matrix}+0&=&00{\color{red}1}1\\+1&=&01{\color{red}0}0\\+2&=&01{\color{red}0}1\\+3&=&01{\color{red}1}0\\+4&=&01{\color{red}1}1\\+5&=&10{\color{red}0}0\\+6&=&10{\color{red}0}1\\+7&=&10{\color{red}1}0\\+8&=&10{\color{red}1}1\\+9&=&11{\color{red}0}0\\\cdots&\cdots&\cdots\end{matrix} $$

按顺序串起来是 $1001100110\cdots$，我们发现，这是以 $0011$ 为循环节的串。

进一步地观察上方表格其它列，我们发现，第 $k$ 低位组成的01串的循环节长度是 $2^{k+1}$，是 $\underbrace{00\cdots0}_{2^k\text{个}}\underbrace{11\cdots 1}_{2^k\text{个}}$

我们考虑对于每一位分别计算贡献。那么，根据题面，对于每一位，它对它的 $0,1,2,\cdots$ 级祖先的贡献，就依次是上面表格中的那一列的值。

而我们要求的是每一个点的异或和，所以说其实对于第 $k$ 位，就是相当于把它的第

$$\begin{matrix}[0\times2^{k+1}+a,0\times2^{k+1}+a+2^k)\cup\\ [1\times2^{k+1}+a,1\times2^{k+1}+a+2^k)\cup\\ [2\times2^{k+1}+a,2\times 2^{k+1}+a+2^k)\cup\\\cdots\end{matrix} $$

级祖先的答案异或上 $2^k$

上面的那些区间可以很容易地根据我们之前找到的规律求出来，（循环节是 $2^{k+1}$，其中有 $2^k$ 个$1$）

而那个 $a$，代表的是一个循环节中的 $\cdots0000{\color{red}1}11\cdots$ 的那个 $\color{red}1$ 的位置。它也可以经过简单的数学推导或者看上面的表格找规律，使用位运算求得。

但怎么维护把上述那么多区间全异或上 $2^k$ 呢？一种简单的想法是使用树上差分，在第

$$\begin{matrix} 0\times2^k+a&1\times2^k+a\\2\times2^k+a&3\times2^k+a\\4\times2^k+a&5\times2^k+a\\\cdots&\cdots\end{matrix}$$

级祖先的差分数组上均异或上 $2^k$，就可以了，这样就可以保证在进入区间的时候答案异或 $2^k$，出区间时再异或回去。

但是我们有这么多的区间，树上差分依然是 $O(n^2)$ 的

但是，观察到，所有要异或 $2^k$ 的差分数组，它们的下标 $\mod 2^k$ 都一样，这就意味着，我们可以开一个新的差分数组，$s_{k,i}$，它等于所有当前dfs到的，深度 $d\mod 2^k=i$ 的所有的点的差分数组。

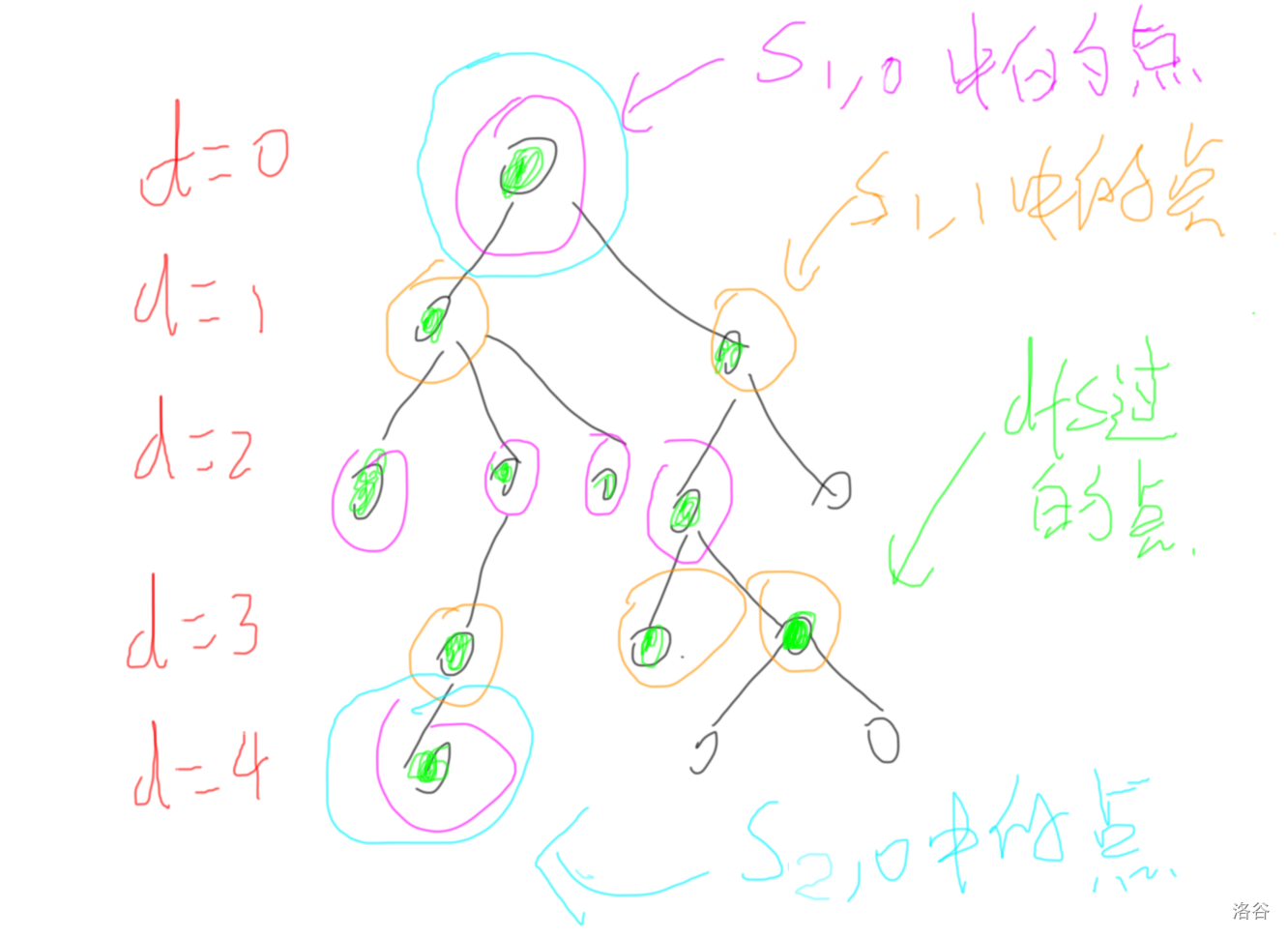
大概是这样（好丑）↑

那么，我们发现，我们修改的那很多的差分，就是单独地改了一个 $s_{k,a}$，这样就是 $O(1)$ 的了

但是怎么找到一个点的差分值呢？我们发现，它的差分值，就等于进入这个点的子树前的 $s_{k,d}$ （$d$为该点深度） 与出该点子树后的 $s_{k,d}$ 的异或差（其实就是异或和）

原因见下图。

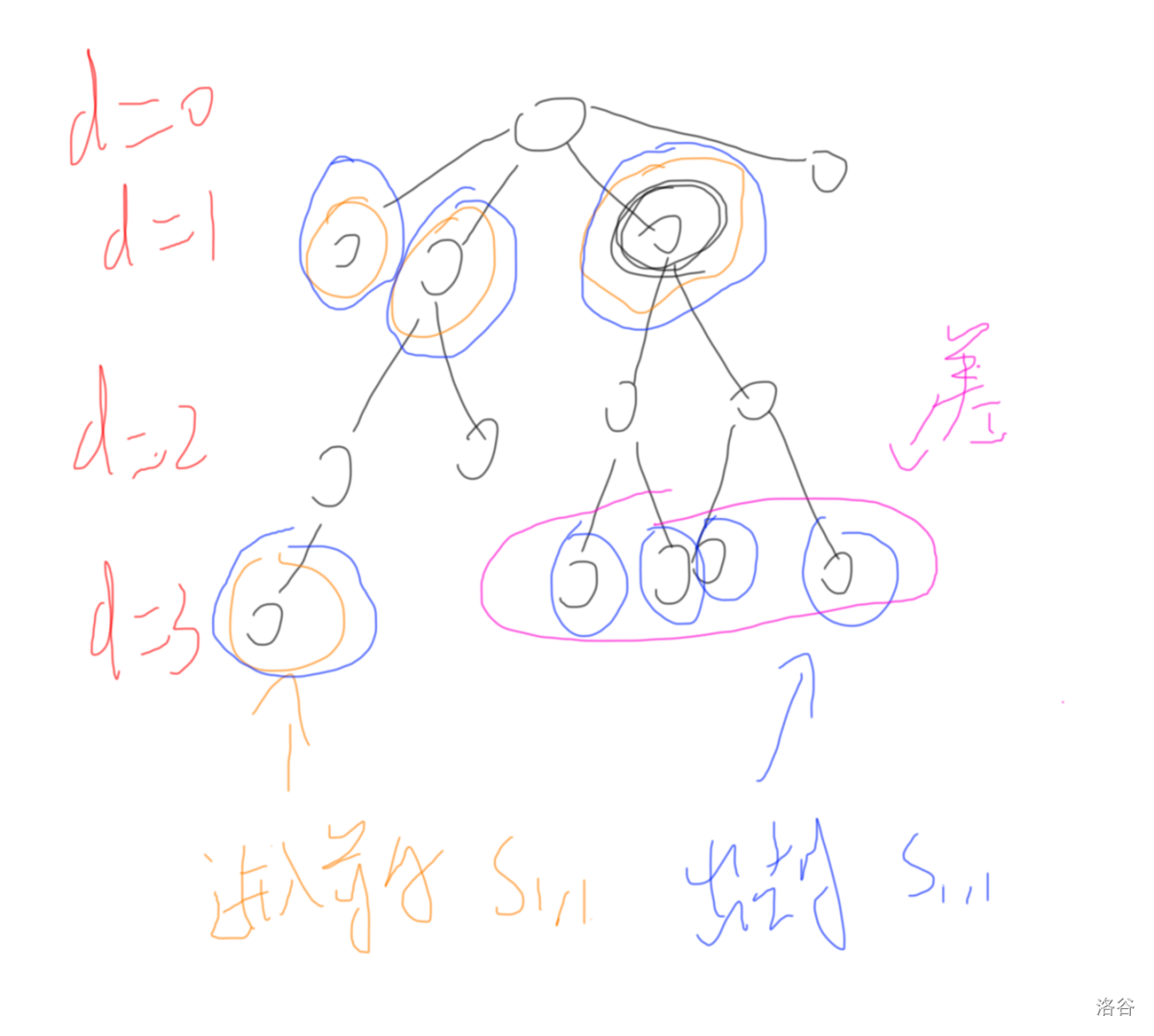
因为我们一个点的差分，就是其子树内的点对于 $s_{k,d}$ 的修改，而这样做差刚好就只算了子树内贡献，所以是对的。

所以，我们对于每一个节点的每一位，都可以 $O(1)$ 地计算贡献和差分数组，所以总复杂度 $O(n\log n)$

上述题解提供的是基础思路，具体的计算和实现可以看代码。

本做法因为只使用了树上差分而没有使用高级数据结构，所以常数很小。

#include<bits/stdc++.h>
using namespace std;
//dengyaotriangle!

const int maxl=21;
const int maxn=1<<maxl;

int n;
unsigned a[maxn];
vector<int> adj[maxn];
unsigned w[maxl][maxn];

unsigned long long tans=0;

unsigned dfs(int u,unsigned d){
    unsigned ans=a[u];
    for(int j=0;j<maxl;j++)w[j][(d+a[u])&((1u<<j)-1u)]^=1u<<j;
    for(int j=0;j<maxl;j++)ans^=w[j][d&((1u<<j)-1u)];
    for(int i=0;i<adj[u].size();i++){
        int v=adj[u][i];
        ans^=dfs(v,d+1);
    }
    for(int j=0;j<maxl;j++)ans^=w[j][d&((1u<<j)-1u)];
    //cerr<<u<<' '<<ans<<endl;
    tans+=ans;
    return ans;
}

int main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=2;i<=n;i++){
        int f;cin>>f;
        adj[f].push_back(i);
    }
    dfs(1,0);
    cout<<tans;
    return 0;
}