自动搬运

查看原文

来自洛谷，原作者为

	pythoner713 Hope deferred maketh the something sick.

搬运于2025-08-24 22:22:17，当前版本为作者最后更新于2020-11-29 22:44:06，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

蒟蒻初学计数DP，这篇题解的代码是照着 lyd 书上的思路写的。希望对初学者有所帮助，望大佬轻喷。

题意十分清晰，求满足三个条件的连通图数量。

乍一眼看难以下手。因为「连通图」「割边」这些概念都是沿用自图论，但问题在于统计图的数量，而这又是一个数论问题。

如果我们从图论角度出发，不难想出一个暴力做法：对于包含 $n$ 个节点的图，一共有 $\frac{n(n-1)}{2}$ 条可能的边，我们二进制枚举每条边是否存在，从而得到所有 $n$ 个节点的图。然后对于每个图，都 $\text{Tarjan}$ 求出割边数量，判断是否符合条件。然而复杂度已经高达 $O(2^{n^2}\times n)$，当场劝退。

于是只能考虑用数学方法计算出答案，这时就要请出计数DP了。

计数DP，顾名思义，就是统计数量的DP。听上去好像没什么，但它统计的一般是诸如「方案数」等更抽象、难以统计的玩意儿，所以思维难度蛮高。光说不练假把戏，我们来到题练练手：

$$\text{求 }n\text{ 个节点的无向联通图有几个？}$$

此处节点有序。是不是跟这题有点像？从DP角度考虑，不妨设 $h[i]$ 表示 $i$ 个节点的无向连通图数量。然后重点来了：由于直接统计有些困难，我们先考虑不合法的方案数，也就是非联通图数，然后用无向图总数减去非联通图数便是答案。

根据上面的分析，每条边可有可无，因此对于 $i$ 个节点，共有 $2^{\frac{i(i-1)}{2}}$ 个无向图。然后对于非联通图来说，我们考虑 $1$ 号节点，它必定属于某个连通块。我们枚举这个连通块的大小 $j$，也就是在剩下 $i-1$ 个节点中选出 $j-1$ 个与节点 $1$ 相连，有$\binom{i-1}{j-1}$ 种选法。而根据定义，这坨大小为 $j$ 的连通块有 $h[j]$ 个不同形态。然后对于外面剩余的 $i-j$ 个节点随意构成无向图，共有 $2^{\frac{(i-j)(i-j-1)}{2}}$ 种方案。因此不合法方案数便是这三者之积：$h[j]\times\binom{i-1}{j-1}\times2^{\frac{(i-j)(i-j-1)}{2}}$。再用总数减去这些非法方案数就，得到了通项公式：

$$h[i]=2^{\frac{i(i-1)}{2}}-\sum_{j=1}^{i-1}h[j]\times\binom{i-1}{j-1}\times2^{\frac{(i-j)(i-j-1)}{2}} $$

代码实现：

	for(int i = 2; i <= n; i++){
		h[i] = qpow(2, i * (i - 1) / 2);
		for(int j = 1; j < i; j++){
			h[i] -= h[j] * C[i - 1][j - 1] % P * qpow(2, (i - j) * (i - j - 1) / 2) % P;
			h[i] = (h[i] % P + P) % P;
		}
	}

（感觉我解释得好烂啊）。这便是计数DP的一道例题了（

我们接下来会发现这个 $h$ 有点用。

回到本题，它只是在上题的基础上加了割边不超过 $m$ 条的限制条件，我们考虑给DP数组多加一维：另 $f[i][j]$ 表示 $i$ 个节点构成的包含 $j$ 条割边的无向连通图数量。先考虑 $j>0$ 如何转移。

没有割边的图就是双联通分量，于是我们照葫芦画瓢，考虑节点 $1$ 所在的双联通分量。我们枚举这个双联通分量的大小 $k$，也就是在剩下的 $i-1$ 个节点中选出 $k-1$ 个节点与 $1$ 构成双联通分量，共有 $f[k][0]\times\binom{k-1}{i-1}$ 种方案（$f[k][0]$ 割边为0，即双联通分量数）。

然后考虑外部节点的连接方案数，我们开一个新数组记录。由于外部节点不一定连通，我们得多开一维记录有几个连通块：令 $g[i][j][k]$ 表示由 $i$ 个节点构成的、有 $j$ 个连通块的、含 $k$ 条割边的无向图数量。其实这个 $g$ 只是 $f$ 的升级版，多了一维记录连通块数量的 $j$ 维度，方便转移。瞧，把每个双联通分量看成一个点，就形成了一棵树，像这样：

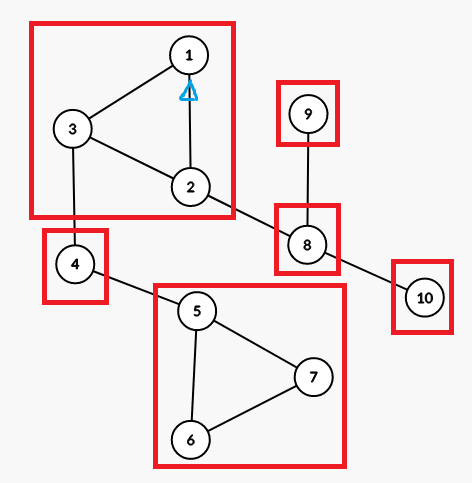
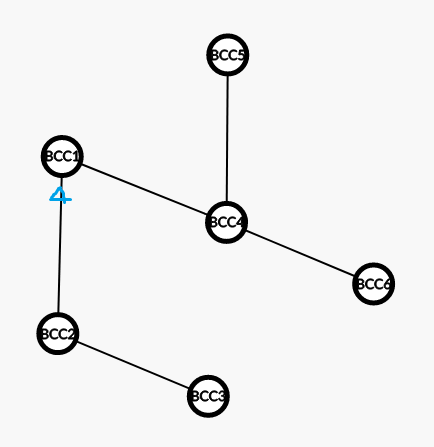
回到 $f[i][j]$，删除了 $1$ 所在这个双联通分量后，还剩 $i-k$ 个节点 。假设还剩 $x$ 个连通块 （在上图中 $x=2$），则还剩下 $j-x$ 个割边 （因为每个连通块贡献一条割边）。留意标斜体的这三处，不正好对应 $g$ 的三个维度吗？即 $g[i-k][x][j-x]$ 。然后外面每个连通块都可以连通到这 $k$ 个点中的任意一个，所以有 $k^x$ 个连接方案。

综上所述，枚举 $x$， 外部节点的方案数即为两者之积之和 $\sum_{x=1}^{\min(i-k,j)}g[i-k][x][j-x]\times k^x$

这时，将外部节点方案数，乘上内部节点方案数 $f[k][0]\times\binom{k-1}{i-1}$ 就得到了总方案数：

$$f[i][j]=\sum_{k=1}^{i-1}\left( f[k][0]\times\binom{k-1}{i-1}\times \sum_{x=1}^{\min(i-k,j)}g[i-k][x][j-x]\times k^x\right) $$

这不就是书上的公式么。那么对于 $j>0$，$f[i][j]$ 就算完了。What about $f[i][0]$ ?

上 $\text{OEIS}$ 找找，$f[i][0]$ 就是 $i$ 个节点构成的双联通分量数量A095983。它不正好等于 $i$ 个点的无向图数量减去至少包含一条割边的无向图数量吗？

惊奇地发现，前者就是本文开篇讲的 $h$ 数组！而后者，根据定义，就是 $f[i][j] (j>0)$ 的和呀。于是我们就有：

$$f[i][0]=h[i]-\sum_{j=1}^{i-1}f[i][j]$$

因此 $f$ 数组的DP顺序其实是 $j>0$ 先，$j=0$ 后：

for(int j = 1; j < i; j++){
			for(int k = 1; k < i; k++){
				int tmp = 0;
				for(int x = 1; x <= min(i - k, j); x++){
					tmp = (tmp + g[i - k][x][j - x] * qpow(k, x) % P) % P;
				}
				f[i][j] = (f[i][j] + f[k][0] * C[i - 1][k - 1] % P * tmp % P) % P;
			}
		}
		f[i][0] = h[i];
		for(int j = 1; j < i; j++){
			f[i][0] -= f[i][j];
			f[i][0] = (f[i][0] % P + P) % P;
		}

最后考虑如何求出 $g[i][j][k]$，我们考虑这 $i$ 个点中编号最小的点所在的连通块。枚举该连通块的大小 $p$ 和割边数量 $q$，则这个连通块的方案数为 $f[p][q]\times \binom{i-1}{p-1}$。我们再在这 $p$ 个点中选一个用于与删掉的双连通块相连，显然有 $p$ 种选法。图中其他部分又有 $g[i-p][j-1][k-q]$ 种方案，所以得到转移方程（由于赶时间搬了段书上原话）：

$$g[i][j][k]=\sum_{p=1}^{i}\sum_{q=0}^{k}f[p][q]\times \binom{i-1}{p-1}\times p\times g[i-p][j-1][k-q] $$

至此，这道题大功告成。

---

$$h[i]=2^{\frac{i(i-1)}{2}}-\sum_{j=1}^{i-1}h[j]\times\binom{i-1}{j-1}\times2^{\frac{(i-j)(i-j-1)}{2}} $$$$f[i][j]=\sum_{k=1}^{i-1}\left( f[k][0]\times\binom{k-1}{i-1}\times \sum_{x=1}^{\min(i-k,j)}g[i-k][x][j-x]\times k^x\right) $$$$f[i][0]=h[i]-\sum_{j=1}^{i-1}f[i][j]$$ $$g[i][j][k]=\sum_{p=1}^{i}\sum_{q=0}^{k}f[p][q]\times \binom{i-1}{p-1}\times p\times g[i-p][j-1][k-q] $$

---

刚才有个朋友问 $\texttt{pythoner713}$ 发生肾么事了，我说怎么回事，给我发了一几张截图。我一看！噢！原来是 $f,g$ 两个数组，一个两维，一个三维。两者间循环更新，是不是要写记忆化搜索？我说不用，只要跟着这 $4$ 个方程依次转移，就可以保证每个状态都恰好更新到。

#include<bits/stdc++.h>
#define int long long
#define P 1000000007
using namespace std;

int ans, n, m, _2[4000], C[60][60], f[60][60], g[60][60][60], h[60];

int qpow(int A, int B){
	int r = 1;
	while(B){
		if(B & 1) r = (r * A) % P;
		A = (A * A) % P, B >>= 1;
	}
	return r;
}

signed main(){
	cin >> n >> m;
	_2[0] = 1;
	for(int i = 1; i <= 2500; i++) _2[i] = (_2[i - 1] << 1) % P;
	for(int i = 0; i <= 50; C[i++][0] = 1){
		for(int j = 1; j <= i; j++){
			C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % P;
		}
	}
	h[1] = 1;
	for(int i = 2; i <= n; i++){
		h[i] = _2[i * (i - 1) / 2];
		for(int j = 1; j < i; j++){
			h[i] -= h[j] * C[i - 1][j - 1] % P * _2[(i - j) * (i - j - 1) / 2] % P;
			h[i] = (h[i] % P + P) % P;
		}
	}
	g[0][0][0] = 1;
	for(int i = 1; i <= n; i++){
		for(int j = 1; j < i; j++){
			for(int k = 1; k < i; k++){
				int tmp = 0;
				for(int x = 1; x <= min(i - k, j); x++){
					tmp = (tmp + g[i - k][x][j - x] * qpow(k, x) % P) % P;
				}
				f[i][j] = (f[i][j] + f[k][0] * C[i - 1][k - 1] % P * tmp % P) % P;
			}
		}
		f[i][0] = h[i];
		for(int j = 1; j < i; j++){
			f[i][0] -= f[i][j];
			f[i][0] = (f[i][0] % P + P) % P;
		}
		for(int j = 1; j <= i; j++){
			for(int k = 0; k < i; k++){
				for(int p = 1; p <= i; p++){
					for(int q = 0; q <= k; q++){
						g[i][j][k] = (g[i][j][k] + (f[p][q] * C[i - 1][p - 1] % P * p % P * g[i - p][j - 1][k - q] % P)) % P;
					}
				}
			}
		}
	}
	for(int i = 0; i <= min(m, n); i++){
		ans = (ans + f[n][i]) % P;
	}
	cout << ans;
	return 0;
}