自动搬运

查看原文

来自洛谷，原作者为

	WanderingTrader 间歇而无奈的自嘲，在否定中重塑自我，如浴火重生的凤凰。——我，程序员

搬运于2025-08-24 22:22:14，当前版本为作者最后更新于2020-06-17 22:17:34，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这题是一道树上操作题，难度不大。

题目分析

其实就是判断一个多叉树中的各子树大小是否相同。
如果以每个节点为根重构树，复杂度将达到$O(n^2)$，在$1\le n\le10^6$的情况下显然是不行的，只能拿到Subtask 1的40分。这样的数据规模要求我们把复杂度降到$O(n\log n)$甚至常数稍大的$O(n)$。
这意味着我们只能执行一次重构树操作，就以节点1为根吧。

我们自造一组强度略高的数据，如下：

7
1 2
3 1
4 2
5 2
4 6
3 7

手算得样例输出：

5 6 7

我们把整棵树画出来即为：

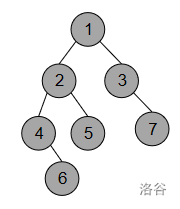
以1为根，计算各结点的子树大小（包含自己）：

7 4 2 2 1 1 1

然后让每个节点找自己子结点的子树大小，以及$n$减去自己大小的值：

4 2
2 1 3
1 5
1 5
6
6
6

我们看到，只有第$5,6,7$行的数字完全相同，满足条件，所以输出5 6 7
大体思路就是这样，主要还是看代码吧。

代码

首先我们用一个邻接表：

#define N 1000005
#define _for(x,y) for(int i = x;i <= y;i ++)
vector <int> es[N];

初始化：

#include <bits/stdc++.h>
using namespace std;
#define N 1000005
#define _for(x,y) for(int i = x;i <= y;i ++)
vector <int> es[N];
bool root[N];
int d[N],n;
int main()
{
	scanf("%d",&n);
	int u,v;
	_for(1,n - 1)
	{
		scanf("%d%d",&u,&v);
		es[u].push_back(v);
		es[v].push_back(u);
	}
	return 0;
}

这里我们对for循环做了一个重定义，主要是想少打几个字吧。

$d[x]$表示$x$的子树大小，$root[x]$表示是否可以作为根。

然后就是模板dfs：

int dfs(int x,int fa)
{
	int size = es[x].size(),num = 0;
	root[x] = 1;
	_for(0,size - 1)
		if(es[x][i] != fa)
		{
			d[x] += dfs(es[x][i],x);
		}
	++ d[x]; 
	return d[x];
}

这里我们用接近$O(n)$的复杂度（每个节点走一次）计算出了各子树的大小，还需要判断能否成为根。

我们使用这个$num$表示比较值，如果$num=0$，直接$num=d[es[x][i]]$（此时已计算完成），否则比较$num$和$d[es[x][i]]$的值，如果不同直接$root[x]=0$。

_for(0,size - 1)
	if(es[x][i] != fa)
	{
		d[x] += dfs(es[x][i],x);
		if(!num)
			num = d[es[x][i]];
		if(num != d[es[x][i]]) root[x] = 0;
	}

然后还要判断$n-d[x]$是否和$num$相等，这里有两点注意：

1. 如果$num$还是0，即x是叶子结点，直接跳过
2. 如果x=1（根节点）直接跳过

代码：

if(x != 1 && num && num != n - d[x]) root[x] = 0;

整个dfs过程：

int dfs(int x,int fa)
{
	int size = es[x].size(),num = 0;
	root[x] = 1;
	_for(0,size - 1)
		if(es[x][i] != fa)
		{
			d[x] += dfs(es[x][i],x);
			if(!num)
				num = d[es[x][i]];
			if(num != d[es[x][i]]) root[x] = 0;
		}
	++ d[x]; 
	if(x != 1 && num && num != n - d[x]) root[x] = 0;
	return d[x];
}

可能有点复杂，但相较于set去重，这种方法常数小一点，时间较为稳定。
做完dfs以后，跑一遍$n$个结点，$root[i]=1$就输出：

dfs(1,0);
_for(1,n)
	if(root[i])
		printf("%d ",i);

全部代码：

#include <bits/stdc++.h>
using namespace std;
#define N 1000005
#define _for(x,y) for(int i = x;i <= y;i ++)
vector <int> es[N];
bool root[N];
int d[N],n;
int dfs(int x,int fa)
{
	int size = es[x].size(),num = 0;
	root[x] = 1;
	_for(0,size - 1)
		if(es[x][i] != fa)
		{
			d[x] += dfs(es[x][i],x);
			if(!num)
				num = d[es[x][i]];
			if(num != d[es[x][i]]) root[x] = 0;
		}
	++ d[x]; 
	if(x != 1 && num && num != n - d[x]) root[x] = 0;
	return d[x];
}
int main()
{
	scanf("%d",&n);
	int u,v;
	_for(1,n - 1)
	{
		scanf("%d%d",&u,&v);
		es[u].push_back(v);
		es[v].push_back(u);
	}
	dfs(1,0);
	_for(1,n)
		if(root[i])
			printf("%d ",i);
	return 0;
}

多叉树的操作题相对二叉树来说可能较为简单，主要就是dfs要写对。有些常见操作（比如求结点大小，求结点深度）等可以打成模板存好，要用的时候 Ctrl+C+V 可以借鉴一下。

$\mathrm{The\ End.}$