自动搬运

查看原文

来自洛谷，原作者为

	犇犇犇犇 菜qaq

搬运于2025-08-24 22:21:55，当前版本为作者最后更新于2020-05-18 22:26:35，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这里是官方题解qaq
这道题其实本质就是个图上的博弈论
核心就是标记必胜点和必败点，只要对着图手动操作一遍就有思路了。个人认为思维难度并不大，但是貌似代码实现上的细节比较多

对于 $10\%$ 的数据，保证图是一条链。

由于是一条链，所以情况是唯一的，直接链表模拟即可。具体见代码。

代码：

#include <bits/stdc++.h>
using namespace std;
int n,m,q,nxt[500005],a,b;
int main()
{
	cin>>n>>m>>q;
	for(int i=1;i<=m;i++)
	{
		cin>>a>>b;
		nxt[a]=b; //由于是链表
	}
	for(int i=1;i<=q;i++)
	{
		cin>>a>>b;
		int k=-1,x=a,f=0; //x表示当前位置，k表示当前走棋的人
		while(nxt[x])
		{
			k=-k; //每次转换走棋的人
			x=nxt[x]; //走到下一个位置
			if(x==b) //到终点
			{
				cout<<k<<endl;
				f=1;
				break;
			}
		}
		if(!f)
			cout<<k<<endl; //如果走到终点，则无法动的人输
	}
	return 0;
}

不难发现这个题是个图上的博弈论的问题。我们自然可以考虑到在图上标记必胜点以及必败点。
首先终点为必败点，所有出度为0的点均为必败点，然后所有能一步到达必败点的点为必胜点，下一步只能到必胜点的点为必败点。于是我们便可以根据这个规则给所有点标记，最后如果起点没有标到，那么就平局。

给张图理解下： 这里有一张图，终点为 $10$，我们从终点开始判断起点的情况。其中必败点标记为红色，必胜点标记为蓝色。

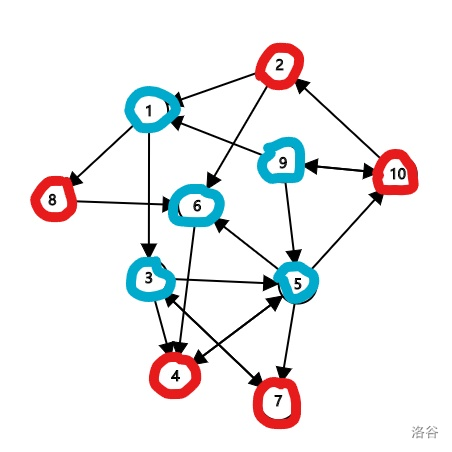
首先，终点10为必败点。9,5能到达10，所以9，5为必胜点。
7，4由于是死路（及走到这个点无路可走）为必败点，标记为红色，于是3，6能到达4，7，故为必胜点。
8能到达的所有点(6)均为必胜点，所以8为必败点。
1能到达必败点8，所以1为必胜点。
2能到达的所有点(1)均为必胜点，所以2为必败点。
这样我们就能得到所有起点的情况了。

对于 $50\%$ 的数据，$1\leq n\leq 10^3$，$1\leq m\leq 2\times10^3$，$1\leq q\leq 10$。

这一档主要就是对于上面那种方法比较暴力的解决方法。每次暴力枚举所有点，看看是否能更新，知道不能更新为止。复杂度 $O(qn^2)$

对于 $70\%$ 的数据，$1\leq n\leq 10^5$，$1\leq m\leq 2\times10^5$，$1\leq q\leq 10$。

这一档就是给一些常数比较大的做法，或者是一些玄学带 log 做法的做法。比如用优先队列判断度数最小的点以及，起点终点搜两遍的做法。

对于 $100\%$ 的数据，$1\leq n\leq 10^5$，$1\leq m\leq 5\times10^5$，$1\leq q\leq 500$。

我们可以发现只要一个点的所有出点的状态（即确定是否为必胜点或必败点）时，那个点的状态我们便能确定。因为若它有一条边指向必败点，则它为必胜点。若它所有边都指向必胜点，那么他就是必败点。所以我们就能想到然后建反向边（因为我们需要从已经确定的点去修改未知的点，即需要知道哪些点会通到它），用一个数组记录它的出度，一个数组记录当前的标记（必胜点或必败点）。
我们用一个队列保存当前可以确定状态的点（即出度为0的点，由于我们只需要讨论反向边的图，所以这里出度即为原图的入度），如果找到一个必败点，那么立即修改所有能通到它的点，把这些点标记为必胜点，并且将能通到这些必胜点的点出度减一。同时我们在减去出度的时候看出度是否为0，如果为0，那么这个点的状态即可确定，放进队列。相当于将已经确定状态的点从图中删去。时间复杂度 $O(qm)$

关于这个时间复杂度，有人私信我说这个复杂度会不会TLE。其实我生成数据的时候在我本地电脑上跑了10s+，但是洛谷评测机上开个O2只用了500ms（我写T4数据的时候也是一样的情况）。

代码：

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 5e5+5;
const int MAXM = 5e5+5;
inline int read()
{
	int x=0,f=1;char c=getchar();
	while(c<'0' || c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();}
	return x*f;	
}
int n,m;
int p[MAXN],vic[MAXN],out[MAXN];
int cnt,head[MAXM],f[MAXN],d[MAXN];
struct edge
{
	int v,nxt;
}e[MAXM*2];
inline void addedge(int u,int v)
{
	cnt++;
	e[cnt].v=v;
	e[cnt].nxt=head[u];
	head[u]=cnt;
}
queue<int> q;
void del(int u)
{
	f[u]=1;
	for(int i=head[u];i;i=e[i].nxt)
	{
		int v=e[i].v;
		d[v]--;
		if(d[v]==0)
			q.push(v);
	}	
} //当前点已经确定状态点删去
int main()
{
	int Q;
	n=read();m=read();Q=read();
	for(int i=1;i<=m;i++)
	{
		int a,b;
		a=read();b=read();
		addedge(b,a); //建反向边
		p[a]++;  //入度
		out[b]++; //出度
	}
	while(Q--)
	{
		int x,y;
		while(!q.empty()) q.pop();
		x=read();y=read();
		memset(f,0,sizeof(f)); 
		memset(d,0,sizeof(d));
		memset(vic,0,sizeof(vic)); //初始化
		for(int i=1;i<=n;i++)
		{
			d[i]=p[i];
			if(p[i]==0) 
				q.push(i); //若当前点出度为0，放进队列
		} 
		q.push(y); //将终点放进队列
		vic[y]=1; //终点为必败点
		while(!q.empty())
		{
			int u=q.front();
			q.pop();
			if(f[u]==1) 
				continue; //已经被访问过
			if(vic[x]!=0)
				break; //小优化，若起点状态已经确定，那就不需要继续搜索了
			del(u); //u已经能确定状态了，将它删去
			if(vic[u]==1)//如果u为必败点，那么所有能通往它的点为必胜点  
			{
				for(int i=head[u];i;i=e[i].nxt) 
				{
					int v=e[i].v;
					if(vic[v]==0)
					{
						vic[v]=-1;
						del(v); //v为必胜点，状态确定，将它删去
					}
				}	
			}
			else if(out[u]==0)
			{
				vic[u]=1; //若u在原图出度为0，则为必败点
			}
			else //u状态未确定
			{
				vic[u]=1; //u能走到的所有点为必胜点，u为必败点
				for(int i=head[u];i;i=e[i].nxt) //将所有能通到必败点标为必胜点
				{
					int v=e[i].v;
					if(vic[v]==0)
					{
						vic[v]=-1;
						del(v); //删去
					}
				}		
			}		
		}
		cout<<-vic[x]<<endl; //输出起点状态
	}
	return 0;
}