Yesterday Once More

0
15011418730 LV 7 @ 2025-8-24 22:21:53
自动搬运

查看原文

来自洛谷，原作者为

zhanghuanrui
网名 Silvefish | We are preparing for the world of tomorrow.

搬运于2025-08-24 22:21:53，当前版本为作者最后更新于2024-11-21 16:28:43，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P6557 Yesterday Once More 题解

原题链接

题意简述

给定一个 $n$ 行 $m$ 列的方格表，其中有一些为障碍格。现在需要用若干个（可以为 $0$ ） $1 \times k$ 或 $k \times 1$ （ $k \ge 2$ ）的长条覆盖方格表，要求长条之间不重叠且不覆盖障碍物。长条并不需要将方格表无障碍的地方完全覆盖。

首先需要输出放置长条的方案数。然后给定 $T$ 次修改（修改之间相互独立），每次修改是下面 $5$ 种之一：
- $1\ x\ y$ ，表示将 $(x,y)$ 的位置设为有障碍。
- $2\ x$ ，表示将第 $x$ 行全部设为有障碍。
- $3\ y$ ，表示将第 $y$ 列全部设为有障碍。
- $4\ x\ y\ t$ ，表示将 $(x,y),(x,y+1),\cdots,(x,y+t)$ 设为有障碍。
- $5\ x\ y\ t$ ，表示将 $(x,y),(x+1,y),\cdots,(x+t,y)$ 设为有障碍。
对于每次修改还需要输出修改过后的方格表的放置方案数。

$1 \le n \le m \le 15$ ， $0 \le T \le 1000$ ，保证 $1,4,5$ 类修改不超过 $100$ 次。

子问题的做法

我们先来考虑对于一次修改要如何求解。本题中长条的放置方式可能会杂乱无章，如果直接记录每个长条的位置，状态数将会是天文数字。

注意到 $n$ 和 $m$ 都很小，因此我们可以尝试使用插头 DP。

我们可以从上往下从左到右依次决定每个无障碍的格子有没有被长条覆盖，以及它被哪个方向的长条覆盖。假设我们目前在考虑第 $i$ 行第 $j$ 列的格子。我们的一种最终方案可能是这样：

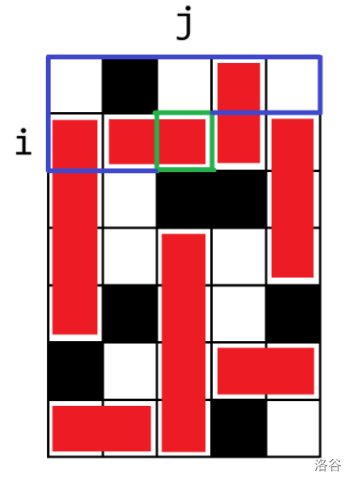
绿色是我们当前正在考虑的格子。那么我们此时就已经确定了上图中蓝色部分的状态。可以发现，蓝色部分对下方仍未确定的方格有影响的只有这一条边界：

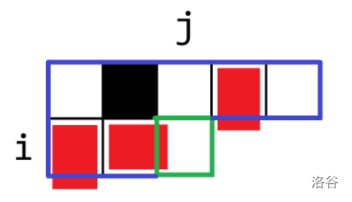
在上图中我们可以看到，有一些红色的长条穿过了边界，这是因为通过蓝色区域得到的信息我们知道这些地方有长条向下延伸，但是我们并不需要知道它们具体在什么地方开始延伸，也不需要立刻确定它们在什么地方停止延伸。我们把像这样的“可能跨过某一条边界延伸”的东西叫做插头。

我们可以发现，任意时刻恰好有 $m+1$ 个可能的插头，其中每列各有一个位置，第 $i$ 行上还有一个（不过这个插头位置有可能在方格表的边界，这时我们就要求它一定不延伸）。因此，我们就可以用一组 $(S,t)$ 表示一组插头的状态，其中 $S$ 表示向下延伸的列构成的集合， $t$ 表示第 $i$ 行的那个插头是否向右延伸。

这时，我们就可以设计 DP 状态了：我们令 $dp_{i,j,S,t}$ 表示我们已经填完 $(i,j)$ 时，此时的插头状态为 $(S,t)$ 的方案数。

转移时，我们可以使用刷表法，即用 $(i,j-1)$ 的状态来更新 $(i,j)$ （当然，我们要用 $(i-1,m)$ 来更新 $(i,1)$ ）。根据 $(i,j-1)$ 位置的插头状态，我们可以通过枚举 $(i,j)$ 是否放置长条以及它的延伸方向进行转移，具体细节可以看代码。

最后的答案就是 $dp_{n,m,\varnothing,0}$ ，因为我们填完最后一个方格的时候，所有的插头必须处于不延伸状态。

高效支持修改

好了，现在我们已经可以求出每次修改的答案了。然而，根据上述分析，求解一组修改的时间复杂度为 $O(nm2^m)$ ，如果对每次修改都进行完整的 DP，总复杂度高达 $O(Tnm2^m)$ ，无法承受。

注意到每次修改至多只会修改一行或一列，而且修改之间相互独立。因此我们在处理修改时，应该有相当多的信息不会改变。

假设我们有这么一个修改：将第 $i$ 行的第 $l$ 至第 $r$ 个格子设为障碍。

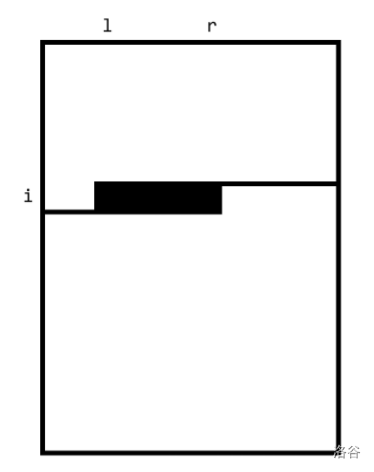
我们可以发现，如果我们还是从上往下从左往右依次考虑每个格子，一直到 $(i,l-1)$ （ $l=1$ 时为 $(i-1,m)$ ）的位置，我们计算出的 DP 数组都会和没有修改时的一样。因此这上半部分可以直接沿用未修改的方格表的 DP 信息。那下半部分怎么办呢？我们只需要对原来的方格表按照从下往上从右往左的顺序再 DP 一遍，就可以直接使用 $(i,r+1)$ （仍然要注意注意边界情况）处的 DP 信息了。

最后，我们还需要枚举两部分边界处的插头状态，由于横向的和第 $[l,r]$ 列的插头已经被障碍物堵住了，因此只可能在 $[1,l-1]$ 和 $[r+1,m]$ 列的插头可以延伸。我们记从上往下的 DP 数组为 $dpl$ ，从下往上的为 $dpr$ ，那么直接枚举这些插头的状态我们就可以得到答案：

$ans=\sum\limits_{S \subseteq \{1,2,\cdots,l-1\}\cup\{r+1,r+2,\cdots,m\}} dpl_{i,l-1,S,0} \times dpr_{i,r+1,S,0}$

注意边界情况的特判。这是处理横向修改的方法。处理纵向修改时，只需要将原方格表旋转 $90 \degree$ 即可。

深挖数据范围

这样，我们似乎就得到了一个 $O(nm+T)(2^m+2^n)$ 的算法，似乎非常紧张。然而，仔细分析，我们就会发现，如果修改类型是整行或整列修改，那么上面式子中的 $\{1,2,\cdots,l-1\}\cup\{r+1,r+2,\cdots,m\}$ 将会变为空集，从而答案的计算过程实际上是 $O(1)$ 的。因此，记 $T'$ 为 $1,4,5$ 类型修改的数量，我们的算法的复杂度实际上是 $O((nm+T')(2^m+2^n)+T)$ 的，可以通过此题。

代码

最后，Talk is cheap, show me the code.

总用时：4.37s

峰值时间：300ms

峰值内存：292.07MB
```
#include <bits/stdc++.h>
#define int long long
#ifdef zhr_debug
#define debug printf
#else
void debug(const char* s,...){}
#endif
using namespace std;
const int mod=998244353;
void add(int &x,int y){x+=y;if(x>=mod)x-=mod;}
void freopen(string file){freopen((file+".in").c_str(),"r",stdin);freopen((file+".out").c_str(),"w",stdout);}
int n,m,qq;
int a[25][25];
struct query
{
	int op;
	int x,y;
	int v;
};
query q[1020];
int ans[1020];
int dpl[17][17][33000][2];
int dpr[17][17][33000][2];
void solve()//进行插头 DP
{
	memset(dpl,0,sizeof(dpl));
	dpl[0][m][0][0]=1;
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
	{
		auto now=dpl[i][j],pre=(j==1 ? dpl[i-1][m] : dpl[i][j-1]);
		for(int s=0;s<(1<<m);s++) for(int t:{0,1})
		{
			if(!pre[s][t]) continue;
			if(t && (s>>j-1&1)) continue;//(i,j) 上方和左方同时需要延伸，矛盾
			if(!a[i][j])
			{
				if(!(t || (s>>j-1&1))) add(now[s][t],pre[s][t]);//当前格为障碍，只有上方和左方同时不要延伸才合法
				continue;
			}
			if(t)
			{
				if(j<m && !(s>>j&1) && a[i][j+1]) add(now[s][t],pre[s][t]);//横向插头向 (i,j+1) 延伸
				add(now[s][0],pre[s][t]);//横向插头不继续延伸
			}
			else if(s>>j-1&1)
			{
				if(i<n && !t && a[i+1][j]) add(now[s][t],pre[s][t]);//纵向插头向 (i+1,j) 延伸
				add(now[s^(1<<j-1)][t],pre[s][t]);//纵向插头不继续延伸
			}
			else
			{
				add(now[s][t],pre[s][t]);//这一格什么也不填
				if(i<n && a[i+1][j]) add(now[s|(1<<j-1)][t],pre[s][t]);//创建一个向 (i+1,j) 延伸的插头
				if(j<m && !(s>>j&1) && a[i][j+1]) add(now[s][1],pre[s][t]);//创建一个向 (i,j+1) 延伸的插头
			}
		}
	}
	memset(dpr,0,sizeof(dpr));
	dpr[n+1][1][0][0]=1;
	for(int i=n;i>=1;i--) for(int j=m;j>=1;j--)
	{
		auto now=dpr[i][j],pre=(j==m ? dpr[i+1][1] : dpr[i][j+1]);
		for(int s=0;s<(1<<m);s++) for(int t:{0,1})
		{
			if(!pre[s][t]) continue;
			if(t && (s>>j-1&1)) continue;
			if(!a[i][j])
			{
				if(!(t || (s>>j-1&1))) add(now[s][t],pre[s][t]);
				continue;
			}
			if(t)
			{
				if(j>1 && !(s>>j-2&1) && a[i][j-1]) add(now[s][t],pre[s][t]);
				add(now[s][0],pre[s][t]);
			}
			else if(s>>j-1&1)
			{
				if(i>1 && !t && a[i-1][j]) add(now[s][t],pre[s][t]);
				add(now[s^(1<<j-1)][t],pre[s][t]);
			}
			else
			{
				add(now[s][t],pre[s][t]);
				if(i>1 && a[i-1][j]) add(now[s|(1<<j-1)][t],pre[s][t]);
				if(j>1 && !(s>>j-2&1) && a[i][j-1]) add(now[s][1],pre[s][t]);
			}
		}
	}
}
int query(int x,int y,int v)
{
	static int ret;ret=0;
	static int yl,yr;yl=y;yr=y+v;
	auto L=(yl==1 ? dpl[x-1][m] : dpl[x][yl-1]),R=(yr==m ? dpr[x+1][1] : dpr[x][yr+1]);
	for(int s=((1<<m)-1)^((1<<yr)-(1<<yl-1));;s=s-1&(((1<<m)-1)^((1<<yr)-(1<<yl-1))))//枚举可能延伸的插头集合
	{
		add(ret,L[s][0]*R[s][0]%mod);
		if(!s) break;
	}
	return ret;
}
signed main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>a[i][j];
	cin>>qq;
	for(int i=1;i<=qq;i++)//将询问离线，因为要横竖各做一遍
	{
		cin>>q[i].op;
		if(q[i].op==2) cin>>q[i].x;
		if(q[i].op==3) cin>>q[i].x;
		if(q[i].op==4) cin>>q[i].x>>q[i].y>>q[i].v;
		if(q[i].op==5) cin>>q[i].x>>q[i].y>>q[i].v;
		if(q[i].op==1) cin>>q[i].x>>q[i].y,q[i].op=4,q[i].v=0;//类型 1 的询问可以转化为类型 4
	}
	solve();
	ans[0]=dpr[1][1][0][0];
	for(int i=1;i<=qq;i++)
	{
		if(q[i].op==2) ans[i]=query(q[i].x,1,m-1);
		if(q[i].op==4) ans[i]=query(q[i].x,q[i].y,q[i].v);
	}
	for(int i=1;i<=max(n,m);i++) for(int j=1;j<i;j++) swap(a[i][j],a[j][i]);
	swap(n,m);solve();//交换横竖再做一遍
	for(int i=1;i<=qq;i++)
	{
		if(q[i].op==3) ans[i]=query(q[i].x,1,m-1);
		if(q[i].op==5) ans[i]=query(q[i].y,q[i].x,q[i].v);
	}
	for(int i=0;i<=qq;i++) printf("%lld\n",ans[i]);
}
```