1 条题解

  • 0
    @ 2025-8-24 22:21:50

    自动搬运

    查看原文

    来自洛谷，原作者为

    avatar 辰星凌
    时过而不知泪已落 —散华礼弥

    搬运于2025-08-24 22:21:50，当前版本为作者最后更新于2020-06-15 11:05:33，作者可能在搬运后再次修改，您可在原文处查看最新版

    自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

    以下是正文

    【题解】Crni [P6551] [SP7884]

    My Blog\mathcal{My}\ \mathcal{Blog}

    传送门：Crni [P6551]\text{Crni [P6551]} [SP7884]\text{[SP7884]}

    【分析】

    这是一道套路题，用到了很多关于矩阵的处理技巧，但找到解决方法后会发现它的思维难度其实并不高，主要是代码实现较困难，所以也可以视其为膜你题。

    【前缀和的套路】

    找子矩阵基本都会用到前缀和，常见的查询子矩阵可以直接容斥，例如维护二维树状数组时用到的方法：

    设 S[x][y]=∑i=1x∑j=1ya[i][j]S[x][y]=\sum_{i=1}^{x} \sum_{j=1}^{y} a[i][j]，那么递推式为 S[i][j]=S[i][j]= S[i−1][j]+S[i][j−1]−S[i−1][j−1]+a[i][j]S[i-1][j]+S[i][j-1]-S[i-1][j-1]+a[i][j]

    如果要查询以 (x1,y1)(x1,y1) 为左下角，以 (x2,y2)(x2,y2) 为右下角的矩阵和，∑i=x1y1∑j=x2y2a[i][j]=\sum_{i={x_1}}^{y_1} \sum_{j={x_2}}^{y_2} a[i][j]= S[x2][y2]−S[x1−1][y2]−S[x2][y1−1]+S[x1−1][y1−1]S[x2][y2]-S[x1-1][y2]-S[x2][y1-1]+S[x1-1][y1-1]

    在预处理式子时需要从左上角一直递推到右下角，而稍复杂一点的需要统计多个方向（没错，就是此题了），即从最多 44 个角落（左上，左下，右上，右下）开始向其对角处递推，得到多个助于统计答案的前缀和数组。

    【预处理】

    回到此题。

    为方便处理，将矩阵中的黑点设为 11，白点设为 00 。

    对于所有的黑点，先预处理出 44 个数组：

    (1).(1). RD[i][j]RD[i][j]： 以 (i,j)(i,j) 为右下角的黑矩阵个数。

    (2).(2). LU[i][j]LU[i][j]： 以 (i,j)(i,j) 为左上角的黑矩阵个数。

    (3).(3). LD[i][j]LD[i][j]： 以 (i,j)(i,j) 为左下角的黑矩阵个数。

    (4).(4). RU[i][j]RU[i][j]： 以 (i,j)(i,j) 为右上角的黑矩阵个数。

    但如果暴力枚举的话 O(n4)O(n^4) 复杂度过高，需要考虑合理继承前面求出的信息。

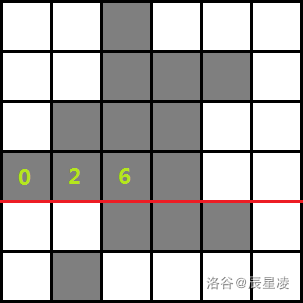
    以 RDRD 为例，为便于推导，我们先在矩阵中枚举一条辅助线，假设已经求出了第 ii 行前 j−1j-1 列的 RDRD 信息，如图为 i=4,j=4i=4,j=4 的情况：

    定义 H[i][j]H[i][j] 为点 (i,j)(i,j) 向上最多可以延伸的距离（或者说高度），如果 a(i,j)a(i,j) 为白块，H[i][j]=0H[i][j]=0 。

    处理方法如下：

    对于点 (i,j)(i,j) 找到同一列前面第一个 HH 小于它的位置 (i,k)(i,k)。

    由于 [k+1,j][k+1,j] 的高度都大于 jj，那么将会有 H[i][j]∗(j−k)H[i][j]*(j-k) 个点可以作为黑矩形的左上角（右下角为 (i,j)(i,j)），但是将 (i,j)(i,j) 自己作为左上角时黑矩阵大小只有 11，所以要减去 11 。

    另外以 (i,k)(i,k) 为右下角的黑矩阵都可以将长度扩大 j−kj-k，即变成以 (i,j)(i,j) 为右下角，但以 (i,k)(i,k) 为右下角的情况没有计算在 RD[i][k]RD[i][k] 以内，所以要加上 11 。

    得到递推式为：RD[i][j]=H[i][j]∗(j−k)−1+RD[i][k]+1RD[i][j]=H[i][j]*(j-k)-1+RD[i][k]+1 。

    于是时间复杂度就被优化到了 O(n3)O(n^3)，但还不够优秀。

    现在的问题是如何快速找 kk，方法同 Largest\text{Largest} Rectangle\text{Rectangle} in\text{in} a\text{a} Histogram\text{Histogram} （题解），直接单调栈维护即可。

    在上面那张图中 H[4][1]=1,H[4][2]=2,H[4][3]=4,H[4][4]=3H[4][1]=1,H[4][2]=2,H[4][3]=4,H[4][4]=3，所以 j=4j=4 时的决策点 k=2k=2，因此 RD[3][4]=3∗2−1+RD[3][2]+1RD[3][4]=3*2-1+RD[3][2]+1 。

    同理可得 LU,LD,RULU,LD,RU 。

    【统计答案】

    依旧是枚举辅助线：

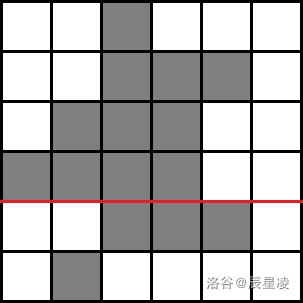
    先求出下边界在红线上面的黑矩形个数，即 ∑i=1x∑j=1nRD[i][j]\sum_{i=1}^{x} \sum_{j=1}^{n} RD[i][j]（或者 LD[i][j]LD[i][j]），

    再求出上边界紧贴在红线下面的黑矩阵个数，即 ∑j=1nLU[x+1][j]\sum_{j=1}^{n}LU[x+1][j]（或者 RU[x+1][j]RU[x+1][j]），

    将二者相乘，再对于每一条辅助线算出的结果求和，得到相对位置为上下的黑矩形总对数。（其实也可以固定红线上面，红线下面求总个数）

    同理枚举竖线，可得相对位置为左右的黑矩形总对数。

    但这样会有算重复的情况，如下图绿色部分和蓝色部分：

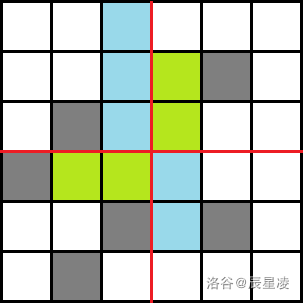
    因此还要减去相对位置既有上下又有左右的黑矩形对数，也就是在十字线对角象限的黑矩形对数，求法和前面大致相同。为方便处理，要任选两个方向计算矩阵前缀和（递推式和二维树状数组的一样）：

    (1).(1). $S_{RD}[x][y]=\sum_{i=1}^{x} \sum_{j=1}^{y} RD[i][j]$
    前缀和递推方向：左上 → 右下 。
    矩阵前缀和意义：右下角在 (i,j)(i,j) 左上面的黑矩阵个数。

    (2).(2). $S_{LU}[x][y]=\sum_{i=n}^{x} \sum_{j=n}^{y} RD[i][j]$
    前缀和递推方向：右下 → 左上 。
    矩阵前缀和意义：左上角在 (i,j)(i,j) 右下面的黑矩阵个数。

    (3).(3). $S_{LD}[x][y]=\sum_{i=1}^{x} \sum_{j=n}^{y} RD[i][j]$
    前缀和递推方向：右上 → 左下 。
    矩阵前缀和意义：左下角在 (i,j)(i,j) 右上面的黑矩阵个数。

    (4).(4). $S_{RU}[x][y]=\sum_{i=n}^{x} \sum_{j=1}^{y} RD[i][j]$
    前缀和递推方向：左下 → 右上 。
    矩阵前缀和意义：右上角在 (i,j)(i,j) 左下面的黑矩阵个数。

    最后，此题细节较多，变量名没设好的话很容易搞混。

    时间复杂度为：O(n2)O(n^2) 。

    【Code】

    #include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#define Re register int
#define For(i,a,b) for(Re i=a;i<=b;++i)
#define Por(i,a,b) for(Re i=a;i>=b;--i)
#define print() for(Re i=1;i<=n;puts(""),++i)for(Re j=1;j<=n;++j)
using namespace std;
const int N=1003,P=10007;
int n,Q[N],A[N][N],H[N][N],SS[N][N];char ch[N];
inline void in(Re &x){
    int f=0;x=0;char c=getchar();
    while(c<'0'||c>'9')f|=c=='-',c=getchar();
    while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
    x=f?-x:x;
}
int RD[N][N];
inline void get_RD(){//RD[i][j]: 以i,j为右下角的黑矩形个数(1,1)→(n,n) 
    memset(H,0,sizeof(H));
    For(i,1,n)For(j,1,n)if(A[i][j])H[i][j]=H[i-1][j]+1;
//  print()printf("%d ",H[i][j]);puts("");
    For(i,1,n){
    	Re h=1,t=0;
    	For(j,1,n)if(!A[i][j])RD[i][j]=-1;
    	RD[i][Q[++t]=0]=-1;
    	For(j,1,n){
            while(h<=t&&H[i][Q[t]]>=H[i][j])--t;
            if(h<=t&&A[i][j])RD[i][j]=RD[i][Q[t]]+1+H[i][j]*(j-Q[t])-1;
            Q[++t]=j;
    	}
    	For(j,1,n)if(RD[i][j]<0)RD[i][j]=0;
    }
//  print()printf("%d ",RD[i][j]);puts("");
}
int LU[N][N];
inline void get_LU(){//LU[i][j]: 以i,j为左上角的黑矩形个数(n,n)→(1,1) 
    memset(H,0,sizeof(H));
    Por(i,n,1)Por(j,n,1)if(A[i][j])H[i][j]=H[i+1][j]+1;
//  print()printf("%d ",H[i][j]);puts("");
    Por(i,n,1){
    	Re h=1,t=0;
    	Por(j,n,1)if(!A[i][j])LU[i][j]=-1;
    	LU[i][Q[++t]=n+1]=-1;
    	Por(j,n,1){
            while(h<=t&&H[i][Q[t]]>=H[i][j])--t;
            if(h<=t&&A[i][j])LU[i][j]=LU[i][Q[t]]+1+H[i][j]*(Q[t]-j)-1;
            Q[++t]=j;
    	}
    	Por(j,n,1)if(LU[i][j]<0)LU[i][j]=0;
    }
//  print()printf("%d ",LU[i][j]);puts("");
}
int LD[N][N];
inline void get_LD(){//LD[i][j]: 以i,j为左下角的黑矩形个数(1,n)→(n,1)
    memset(H,0,sizeof(H));
    For(i,1,n)Por(j,n,1)if(A[i][j])H[i][j]=H[i-1][j]+1;
//  print()printf("%d ",H[i][j]);puts("");
    For(i,1,n){
    	Re h=1,t=0;
    	Por(j,n,1)if(!A[i][j])LD[i][j]=-1;
    	LD[i][Q[++t]=n+1]=-1;
    	Por(j,n,1){
            while(h<=t&&H[i][Q[t]]>=H[i][j])--t;
            if(h<=t&&A[i][j])LD[i][j]=LD[i][Q[t]]+1+H[i][j]*(Q[t]-j)-1;
            Q[++t]=j;
    	}
    	Por(j,n,1)if(LD[i][j]<0)LD[i][j]=0;
    }
//  print()printf("%d ",LD[i][j]);puts("");
}
int RU[N][N];
inline void get_RU(){//RU[i][j]: 以i,j为右上角的黑矩形个数(n,1)→(1,n)
    memset(H,0,sizeof(H));
    Por(i,n,1)Por(j,n,1)if(A[i][j])H[i][j]=H[i+1][j]+1;
//  print()printf("%d ",H[i][j]);puts("");
    Por(i,n,1){
    	Re h=1,t=0;
    	For(j,1,n)if(!A[i][j])RU[i][j]=-1;
    	RU[i][Q[++t]=0]=-1;
    	For(j,1,n){
            while(h<=t&&H[i][Q[t]]>=H[i][j])--t;
            if(h<=t&&A[i][j])RU[i][j]=RU[i][Q[t]]+1+H[i][j]*(j-Q[t])-1;
            Q[++t]=j;
    	}
    	For(j,1,n)if(RU[i][j]<0)RU[i][j]=0;
    }
//  print()printf("%d ",RU[i][j]);puts("");
}
inline int U_D(){//加上-下 
    Re ans=0,S=0;
    For(i,1,n){
    	For(j,1,n)(ans+=S*LU[i][j]%P)%=P;//用【左上角为(i,j)的矩阵LU】固定在辅助线下面
    	For(j,1,n)(S+=RD[i][j])%=P;//用【右下角为(i,j)的矩阵RD】求辅助线上边的总个数
    }
    return ans%P;
}
inline int L_R(){//加左-右 
    Re ans=0,S=0;
    For(j,1,n){
    	For(i,1,n)(ans+=S*LU[i][j]%P)%=P;//用【左上角为(i,j)的矩阵LU】固定在辅助线右边
    	For(i,1,n)(S+=RD[i][j])%=P;//用【右下角为(i,j)的矩阵RD】求辅助线左边的总个数
    }
    return ans%P;
}
inline int LU_RD(){//减左上-右下 
    Re ans=0;memset(SS,0,sizeof(SS));
    For(i,1,n-1)For(j,1,n-1){
    	SS[i][j]=((RD[i][j]+SS[i-1][j]+SS[i][j-1])%P-SS[i-1][j-1]+P)%P;
    	//十字线左上角的用【右下角为(i,j)的矩阵RD】求总和
    	(ans+=SS[i][j]*LU[i+1][j+1]%P)%=P;//用【左上角为(i,j)的矩阵LU】固定十字线的右下角
    }
    return ans;
}
inline int RU_LD(){//减右上-左下 
    Re ans=0;memset(SS,0,sizeof(SS));
    For(i,1,n-1)Por(j,n,2){
    	SS[i][j]=((LD[i][j]+SS[i-1][j]+SS[i][j+1])%P-SS[i-1][j+1]+P)%P;
    	//十字线右上角的用【左下角为(i,j)的矩阵LD】求总和
    	(ans+=SS[i][j]*RU[i+1][j-1]%P)%=P;//用【右上角为(i,j)的矩阵RU】固定十字线的左下角
    }
    return ans;
}
int main(){
//  freopen("crni.in","r",stdin);
//  freopen("crni.out","w",stdout);
    in(n);
    For(i,1,n){
    	scanf("%s",ch+1);
    	For(j,1,n)A[i][j]=(ch[j]=='C');
    }
    get_RD(),get_LU(),get_LD(),get_RU();
    printf("%d\n",((U_D()+L_R())%P-(LU_RD()+RU_LD())%P+P)%P);
//  fclose(stdin);
//  fclose(stdout);
    return 0;
}
    • 1

    [COCI 2010/2011 #2] CRNI

    信息

    ID
    5534
    时间
    1000ms
    内存
    128MiB
    难度
    6
    标签
    递交数
    0
    已通过
    0
    上传者
    1. 关于
    2. 联系我们
    3. 隐私
    4. 服务条款
    5. Language
    6. 主题
    3. Worker 0, 30ms