自动搬运

查看原文

来自洛谷，原作者为

	yzc2005 いつの日か粉になって散るだけ

搬运于2025-08-24 22:21:47，当前版本为作者最后更新于2020-07-29 16:54:13，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

一、定义

• 点：每个方格的四个角
• 一种筑墙方案的区域：被墙框柱的点集

我们的任务即是要确定一种合法的筑墙方案（其区域包含了所有关键方格的四个角），使得筑墙的代价最小

二、引理

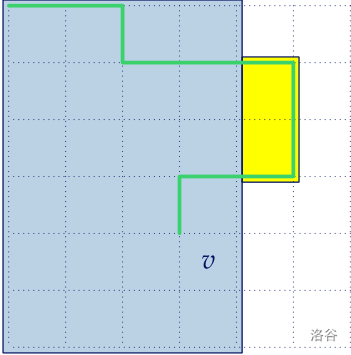
• 此筑墙方案一定包含最左上角的点到每个方格的左上角的点的最短路。

• 证明：

我们用归纳调整的思想。假设我们已经求出一个合法的筑墙方案，且存在一个关键方格 $u$，满足左上角到此点左上角的最短路不被包含在区域内。显然地，此最短路一定被这道墙分割成了若干段，在墙内的段和在墙外的段交替出现。我们把区域扩展到在墙外的段（即用这部分在墙外的段代替连接这一段两端点的墙的部分），相当于把原墙和最短路部分合并。这样，不仅墙的区域扩大了，而且由最短路的定义，新方案的代价肯定不劣于原方案。于是新的方案肯定不劣。一直这样调整下去直到无法继续进行优化，最终得到的结果便满足原命题的任意一个状态。

引理即得证。

三、做法

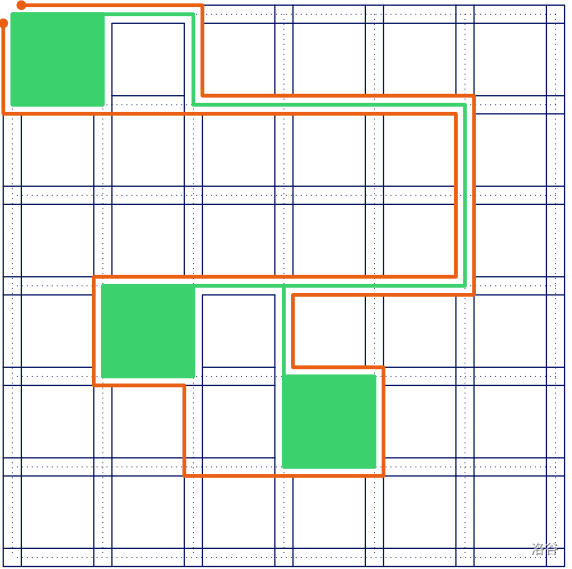
现在我们的任务就是，给定一些最短路，求出包含这些最短路（即墙的区域包含所有最短路上的点）的方案的最小代价。

又因为所有最短路构成了一棵最短路树，所以我们只要满足筑墙方案不穿过最短路即可。考虑把每一个点再拆成四个小点（一个方格对应 16 个点），在原图基础上再在相邻的、不穿过任意一条最短路树的边两点之间连一条边权为 0 的边，跑最短路即可。

四、代码

实在太难实现了，先鸽子了.jpg（