自动搬运

查看原文

来自洛谷，原作者为

	MarchKid_Joe 3.17 the last day

搬运于2025-08-24 22:21:32，当前版本为作者最后更新于2022-09-20 22:34:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P6517 [CEOI2010 day1] alliances

算法

• 网络流黑白染色

题目

一共给出了 $4$ 种限制。

第 $1$ 种结点：与四连通的 $1$ 个邻居 Union。

第 $2$ 种结点：与四连通的 $2$ 个邻居 Union。

第 $3$ 种结点：与四连通的 $3$ 个邻居 Union。

第 $4$ 种结点：与四连通的 $4$ 个邻居 Union。

但是第 $2$ 种结点还有一个坑：就是不能同时与上下或左右 Union。

最后输出一种可行方案。

思路

看到这种配对的问题，自然要考虑网络流黑白染色思想了。

规定：对于二元组 $(i,j)$，若 $i+j$ 为奇数，则为黑点；否则，为白点。而且：黑点只向白点连边，但是白点不向黑点连边。

有无解

判断是否有解只需要判断：黑点的权值和是否等于结盟数（也就是最大流）。

建图

初始化

源点 $s$ 向所有黑点连边，权值为输入的数据。

所有白点向汇点 $t$ 连边，权值为输入的数据。

联盟关系

分为两部分：

先考虑不包括第 $2$ 种结点的情况（非人类点）：

首先，判断黑白点，若是白点，跳过；否则：黑点向白点连边，权值为 $1$。

再考虑包括第 $2$ 种结点的情况：

发现人类比较特殊，含有两条限制：不能同时与上下或左右 Union。

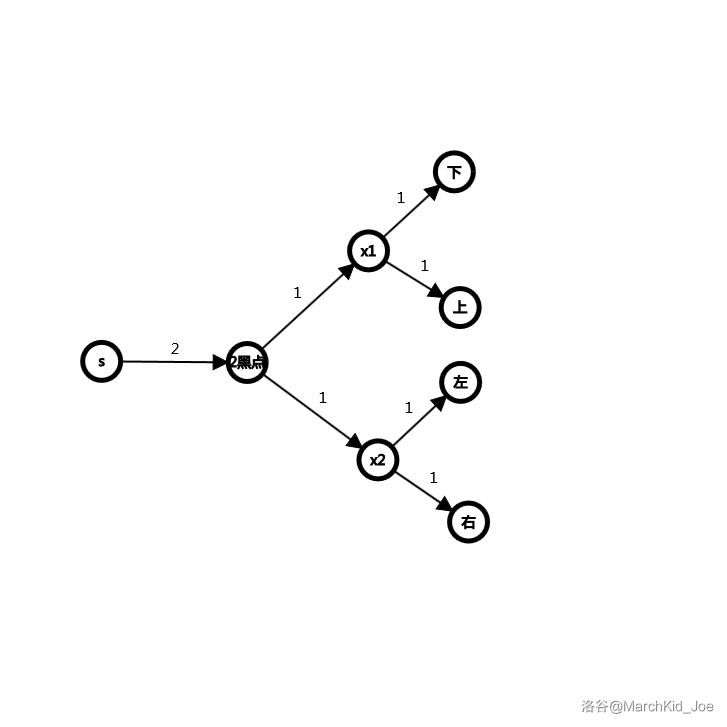
那我们只需要把人类拆为 $3$ 个点：第一个为初始点 $x$，第二个为管理上下方向的结点 $x_1$，第三个为管理左右的结点 $x_2$。

对于初始点，仍然限流为 $2$。

对于其他两个结点：

若此节点为黑点：

从初结点分别向 $x_1$ 和 $x_2$ 连接一条权值为 $1$ 的边。然后 $x_1$ 向这个结点的上下结点连边，权值为 $1$；$x_2$ 向这个结点的左右结点连边，权值为 $1$。

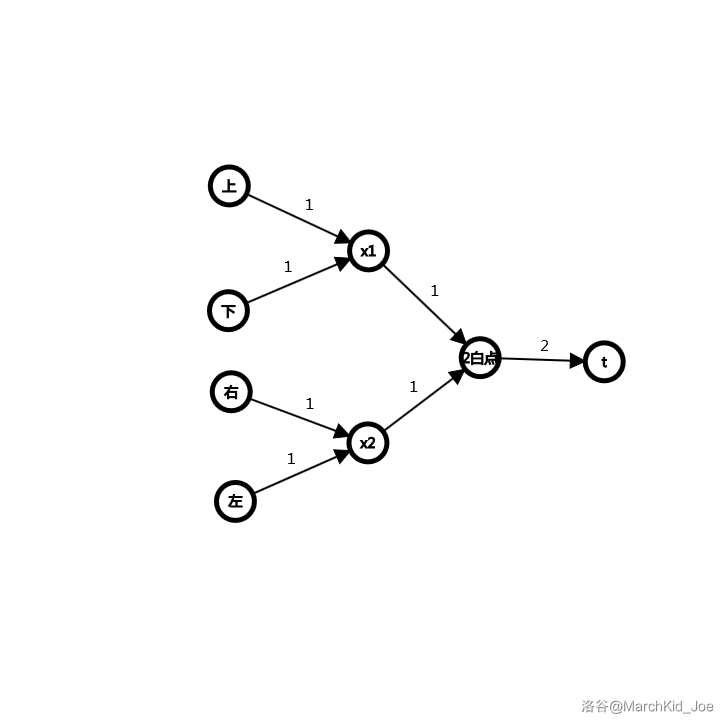
若此节点为白点：

从 $x_1$ 和 $x_2$ 分别向初结点连接一条权值为 $1$ 的边。然后这个结点的上下结点向 $x_1$ 连边，权值为 $1$；这个结点的左右结点向 $x_2$ 连边，权值为 $1$。

发现黑白点就是反着建图。

建图总结

源点 $s$ 向黑点连边。

白点向汇点 $t$ 连边。

黑点向白点连边。

把第 $2$ 种结点——人类拆了。

最大流

网络流模板。

统计答案

正边没有流或者反边有流则证明这条边连接的两个结点 Union。

提醒

注意普通点 $1,3,4$ 向人类点 $2$ 连边时不是向初始点 $x$ 连边，而是向另外两个管辖方向的点连边。（我吃亏了）

网络流反边流量为 $0$。（我又吃亏了）

答案的图的大小是原图的 $3$ 倍。（我又双吃亏了）

最好将 $(1,1)$ 结点设为黑点，这样就不用特判只有一个点的情况了（不特判 $98$ 分）。因为如果 $(1,1)$ 是白点，黑点贡献（联盟数量）为 $0$，最大流也是 $0$，就判断为有解了，显然错误。（我又双叒吃亏了）

编号方式：

$n$ 行 $m$ 列：

对于二元组 $(i,j)$，编号为 $i\times(m-1)+j$。

对于第 $k$ 个人类的管辖方向的点，编号为 $n\times m+2\times k-x\qquad x\in[0,1]$。

统计答案时要原图结点的坐标，开个桶，下标为二元组对应的编号，内容存相应的二元组就行了。

这是我的编号方式。（这次没吃亏）

Code

#include <bits/stdc++.h>
using namespace std;
#define judge ((i + dx[k] >= 1 && j + dy[k] >= 1 && i + dx[k] <= n && j + dy[k] <= m) && (a[i + dx[k]][j + dy[k]]))
//judge 判断是否越界，是否为无人区。
const int inf = 1 << 30;
const int N = 70 + 5;
const int M = 3 * N * N;
const int s = M - 1;//原点
const int t = M - 2;//汇点
namespace IO
{
    struct type//二元组，其实就是pair<int,int>
    {
        int x, y;
        friend bool operator<(const type &A, const type &B){return A.x != B.x ? A.x < B.x : A.y < B.y;}
        type(int x = 0, int y = 0) : x(x), y(y){}
    };
    template <typename Type> void read(Type &n)
    {
        Type w=1;char x=getchar();n=0;
        while(x<'0'||x>'9'){if(x=='-')w=-1;x=getchar();}
        while(x>='0'&&x<='9'){n=(n<<1)+(n<<3)+(x^48);x=getchar();}
        n*=w;
    }
    template <typename Type,typename...Etc> void read(Type &n,Etc &...etcs)
    {
        read(n);read(etcs...);
    }
    template <typename Type> void write(Type x)
    {
        if(x<0) putchar('-'),x=-x;
        if(x>9) write(x/10);
        putchar(x%10+'0');
    }
}
using namespace IO;
namespace network//网络流模板，此部分不解释
{
    struct edge
    {
        int u;
        int v;
        int w;
        int nxt;
        edge(int u = 0, int v = 0, int w = 0, int nxt = 0) : u(u), v(v), w(w), nxt(nxt){}
    };
    edge e[M << 4];
    int head[M];
    int dep[M];
    int cur[M];
    int ecnt = 1;
    void add(int u, int v, int w)
    {
        e[++ecnt] = edge(u, v, w, head[u]); head[u] = ecnt;
        e[++ecnt] = edge(v, u, 0, head[v]); head[v] = ecnt;
    }
    bool bfs()
    {
        queue<int> q;
        memcpy(cur, head, sizeof(cur));
        memset(dep, 0, sizeof(dep));
        dep[s] = 1;
        q.push(s);
        while (!q.empty())
        {
            int u = q.front();
            q.pop();
            for (int i = head[u]; i; i = e[i].nxt)
            {
                int v = e[i].v;
                if (e[i].w && !dep[v])
                {
                    dep[v] = dep[u] + 1;
                    q.push(v);
                }
            }
        }
        return dep[t];
    }
    int dfs(int u, int flow)
    {
        if (u == t)
            return flow;
        int i, rest = flow;
        for (i = cur[u]; i; i = e[i].nxt)
        {
            int v = e[i].v;
            if (e[i].w && dep[v] == dep[u] + 1)
            {
                int k = dfs(v, min(e[i].w, rest));
                rest -= k;
                e[i].w -= k;
                e[i ^ 1].w += k;
                if (!rest)
                    break;
            }
        }
        cur[u] = i;
        return flow - rest;
    }
    int maxflow()
    {
        int ans = 0;
        while (bfs())
            ans += dfs(s, inf);
        return ans;
    }
}
using namespace network;
int n, m, sum;
int a[N][N], b[N * 3][N * 3];//原图和答案图，记得开 3 倍
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
//下，上，右，左
int personcnt;
//人的个数
map<type, type> person;
//人拆出来的两个管辖方向的点
map<type, bool> Union;
//判断两个点是否联合。
type point[M];
//桶存相应的点的坐标
bool black(type p)//判断是否为黑点
{
    return !((p.x + p.y) & 1);
}
int get_num(type p)//得到二元组的编号
{
    return (p.x - 1) * m + p.y;
}
void get_edge()//建边
{
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            read(a[i][j]);
            type now = type(i, j);
            sum += a[i][j] * black(now);
            if (black(now))//s->黑点
                add(s, get_num(now), a[i][j]);
            else//白点->t
                add(get_num(now), t, a[i][j]);
            point[get_num(now)] = now;
            if (a[i][j] == 2)
            {
                ++personcnt;//人类+1
                person[now] = type(n * m + 2 * personcnt - 1, n * m + 2 * personcnt);//拆点
                point[person[now].x] = now;
                point[person[now].y] = now;
                if (black(now))//黑点->x1,x2
                {
                    add(get_num(now), person[now].x, 1);
                    add(get_num(now), person[now].y, 1);
                }
                else//x1,x2->白点
                {
                    add(person[now].x, get_num(now), 1);
                    add(person[now].y, get_num(now), 1);
                }
            }
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            type u = type(i, j);
            if (!black(u) || a[i][j] == 0)
                continue;//白点，无人区不连边
            for (int k = 0; k < 4; k++)
            {
                type v = type(i + dx[k], j + dy[k]);
                if (judge)
                {
                    if (a[i + dx[k]][j + dy[k]] == 2)//连向的点是人类
                    {
                        if (a[i][j] == 2)//当前点是人类
                        {
                            if (k < 2)//上下
                                add(person[u].x, person[v].x, 1);
                            else//左右
                                add(person[u].y, person[v].y, 1);
                        }
                        else//当前点是普通点
                        {
                            if (k < 2)
                                add(get_num(u), person[v].x, 1);
                            else
                                add(get_num(u), person[v].y, 1);
                        }
                    }
                    else//连向的点是普通点
                    {
                        if (a[i][j] == 2)
                        {
                            if (k < 2)
                                add(person[u].x, get_num(v), 1);
                            else
                                add(person[u].y, get_num(v), 1);
                        }
                        else
                            add(get_num(u), get_num(v), 1);
                    }
                }
            }
        }
    }
}
void get_map()
{
    for (int i = 1; i <= n * 3; i++)
        for (int j = 1; j <= m * 3; j++)
            b[i][j] = '.';//初始化全部没人
    for (int i = 2; i <= ecnt; i += 2)//Union
    {
        if (e[i].u != s && e[i].v != t && !e[i].w)
        {
            int u = get_num(point[e[i].u]);
            int v = get_num(point[e[i].v]);
            Union[type(u, v)] = true;
            Union[type(v, u)] = true;
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            if (a[i][j])//若当前不是无人区
            {
                int xl = 3 * (i - 1) + 1, xr = 3 * i;
                int yl = 3 * (j - 1) + 1, yr = 3 * j;
                int xmid = (xl + xr) >> 1, ymid = (yl + yr) >> 1;
                b[xmid][ymid] = 'O';
                for (int k = 0; k < 4; k++)
                    if (judge && Union.count(type(get_num(type(i, j)), get_num(type(i + dx[k], j + dy[k])))))//判断四个方向是否 Union
                        b[xmid + dx[k]][ymid + dy[k]] = 'X';
            }
        }
    }
}
signed main()
{
    int total = 0;
    read(n, m);
    get_edge();//建边
    if (sum != maxflow())//判断
    {
        printf("Impossible!");
        return 0;
    }
    get_map();//答案
    for (int i = 1; i <= n * 3; i++)//print
    {
        for (int j = 1; j <= m * 3; j++)
        {
            putchar(b[i][j]);
        }
        putchar('\n');
    }
    return 0;//never give up.
}

后言

感谢

ao 对本人错误思想的指出及正确思想的提供。

感谢管理员大大抽出时间审核。