自动搬运

查看原文

来自洛谷，原作者为

	command_block 众水皆昂首，饮月唯我一。

搬运于2025-08-24 22:20:56，当前版本为作者最后更新于2020-04-20 08:15:00，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

• 原版 : P5617 [MtOI2019]不可视境界线

建议去看看我的题解,可以帮助理解本文。关于面积计算和预处理就不赘述了。

首先这是有决策单调性的。前置芝士 : DP的决策单调性优化总结

• 方法0

  考虑枚举起点,断环为链,就变成了原版问题。

  那么显然有$O(n^2k)$的背包做法,总复杂度就是$O(n^3k)$.

  为了方便对拍这里给出代码:

#include<algorithm>
#include<cstdio>
#include<cmath>
#include<ctime>
#define db long double
using namespace std;
const db Pi=acos(-1);
inline int read(){
  register int X=0;
  register char ch=0;
  while(ch<48||ch>57)ch=getchar();
  while(ch>=48&&ch<=57)X=X*10+(ch^48),ch=getchar();
  return X;
}
int n,k,R,L,x[2050],s[1050],tp[1050][1050];
db cir,f[1050][1050],ts[40500];
inline db c(int b,int a){
  if (x[b]-x[a]>=R+R)return cir+(x[b]-x[a])*1e-10;
  return ts[x[b]-x[a]];
}
int st[1050];
db ans;
void calc(int bg)
{
  f[1][1]=cir;
  for (int i=2;i<=n+1;i++)
    for (int j=2;j<=k+1;j++){
      f[i][j]=0;
      for (int p=1;p<i;p++){
        db sav=f[p][j-1]+c(i,p);
        if (sav>f[i][j]){
          f[i][j]=sav;
          tp[i][j]=p;
        }
      }
    }
  db tmp=f[n+1][k+1]-cir;
  if (tmp>ans){
    ans=tmp;
    for (int p=tp[n+1][k+1],c=k;p;p=tp[p][c--])
      st[c]=p;
    for (int i=1;i<=k;i++)st[i]=(st[i]+bg-2+n)%n+1;
    sort(st+1,st+k+1);
  }
}
int main()
{
  if (n>1000)return 0;
  n=read();k=read();R=read();L=read();
  cir=Pi*R*R;
  for (int i=1;i<=R+R;i++)
    ts[i]=(Pi-acos(0.5*i/R)*2)*R*R+sqrt(R*R-i*i*0.25)*i;
  for (int i=1;i<=n;i++)
    s[i+n]=(s[i]=read())+L;
  x[0]=-100000;
  db ans=0;
  for (int i=0;i<n;i++){
    for (int j=1;j<=n+1;j++)
      x[j]=s[i+j];
    calc(i+1);
  }
  for (int i=1;i<=k;i++)
    printf("%d ",st[i]);
  return 0;
}

• 方法①

  更快地解决原问题,层单调性分治分治即可$O(nklogn)$,或者原问题的WQS+二分队列做到$O(n\log S\log n)$

  总复杂度是$O(n^2k\log n)$或者$O(n^2\log S\log n)$.

• 方法②

  考虑路径交错,先$O(nk\log n)$单调性分治求出任意一种方案,然后剩余的所有方案就都是交错的。

  选取最短的(决策点最少)一段,这一段的长度是$O(n/k)$的,在这一段里面枚举起点即可。

  这样是$O(n/k)$个原问题,每个的复杂度是$O(nk\log n)$,总复杂度是$O(n^2\log n)$.

接下来是$O(n\log S\log n+n\log^2n)$的魔法。

先考虑如何快速求出任意一种钦定起点的方案。当然直接大力分治就可以$O(nk\log n)$。

根据原题这是凸的,使用WQS二分+二分队列即可做到$O(n\log n\log S)$。

但是可能在构造方案上遇到一点麻烦……

可以对圆的位置玄学扰动避免答案凸包三点共线,这样会导致预处理失效引来巨大的时间常数。

考虑仔细分析。

计算扰动对面积的影响时,可以先算出接触弧长,再计算扰动距离。

由于扰动距离很小,扰动后接触弧长变化不大,所以两者相乘即为误差极小的答案。

然后弄个pair,如果两种转移原值差距不超过 $eps$ ,则比较扰动损失。

多随机几次应该就能得到恰为$k$个的方案了。

注意,如果能够选出不相交的$k$个圆,扰动也就失效了,此时需要特判。

似乎有比较系统的构造方法……改日再学吧。

由于这是乱搞,精度比较玄学,需要long double和玄学调 $eps$,具体可以看代码。

得到了一种方案之后,由于路径交错,可以把每个点的决策区间划分出来,其长度总和是$O(n)$的。

注意,两个端点都要包含,所以可能会产生一些边界情况。

考虑把一段段的决策区间拆下来分层排成一排,则有这样的模式:

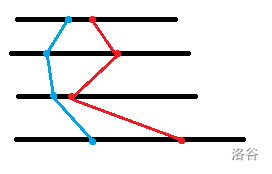
一条折线则表示某种钦定起始点的最优决策,不难发现折线相交就代表着路径不交错,所以所有折线都是不交的。

现在重头戏来了,我们对起始点分治,对于后面的点采用一般的决策单调性分治。

我们会得到一条折线,把所有的层分成了两部分,大小和为$O(n)$,于是分治下去找折线,决策区间长度总和是$O(n\log n)$的。

注意,正好在分界线上的点是分不清在哪一边的,所以有$O(k)$的额外花费。

我们把起点选在最短的一段,这部分花费就是最坏$O(n/k*k)=O(n)$的了。

当然内层还有普通的决策单调性分治,所以复杂度是$O(n\log^2n)$

由于我们真正做DP的时候会拆环为链,有可能最后一块的决策恰为第一个圆,此时需要特判。

折腾了两天终于写完了……

总结一下坑点吧:

• 需要预处理几何部分躲掉大常数。

• 玄学的 $eps$.

• 找到最短的一段之后,要把坐标和下标旋转一下方便处理。

• 决策区间同时包含两个端点,所以是会略微重合的,DP的时候需要滚动数组。

• 可能最后一段包含了第一个圆,这是需要特判的。

#include<algorithm>
#include<cstdio>
#include<cmath>
#define db long double
#define MaxN 100500
using namespace std;
const db Pi=acos(-1);
inline int read(){
  register int X=0;
  register char ch=0;
  while(ch<48||ch>57)ch=getchar();
  while(ch>=48&&ch<=57)X=X*10+(ch^48),ch=getchar();
  return X;
}
int n,cnt,R,x[MaxN];
db f[MaxN],fl[MaxN],ts[MaxN],tl[MaxN],cir;
//a -> b
inline db c(int b,int a){
  // 实际面积 
  if (x[b]-x[a]>=R+R)return f[a]+cir;
  return f[a]+ts[x[b]-x[a]];
}
int tp[MaxN];
inline db rc(int b,int a){
  // 扰动权值 
  if (x[b]-x[a]>=R+R)return fl[a];
  return fl[a]+tl[x[b]-x[a]]*(tp[b]-tp[a]);
}
bool flag;//是否计入扰动 
db eps;
bool cmp(int p,int x,int y){
  db cx=c(p,x),cy=c(p,y);
  if (flag||cx-cy>eps||cy-cx>eps)
    return cx>cy;
  return rc(p,x)>rc(p,y)+eps;
}
int query(int i,int j)
{
  int l=max(i,j),r=min(n,l+R),mid;
  while(l<r){
  	mid=(l+r)>>1;
  	if (cmp(mid,i,j))r=mid;
  	else l=mid+1;
  }if (r==n)return n+cmp(n,j,i);
  return r;
}
int k[MaxN],stk[MaxN],p[MaxN],tot;
db ans,mid,mid2;
void check()
{
  int l=1,r=1;stk[1]=0;
  for (int i=1;i<=n;i++){
  	while(l<r&&k[l+1]<=i)l++;
  	f[i]=c(i,p[i]=stk[l])+mid;
  	fl[i]=rc(i,p[i])+mid2;
  	while(l<r&&k[r]>=query(i,stk[r]))r--;
    stk[++r]=i;k[r]=query(i,stk[r-1]);
  }int tp=n;tot=0;
  while(tp){tp=p[tp];tot++;}
  ans=f[n];
}
int L;
void adjust()
{
  for (int i=1;i<=n;i++)
    tp[i]=(rand()<<12^rand())%10000000;
  //随机扰动并再次WQS
  double l=-R*1e8,r=R*1e8;
  for (int qt=0;qt<=45&&tot!=cnt;qt++){
    mid2=(l+r)/2;check();
    //printf("%d %.8lf\n",tot,(double)mid2);
    if (tot>cnt)r=mid2;
    if (tot<cnt)l=mid2;
  }
}
int st[MaxN];
bool getone()
{
  tot=0;
  db l=-cir,r=0;flag=1;
  while(r-l>eps*1e-4&&tot!=cnt){
    mid=(l+r)/2;check();
    if (tot>cnt)r=mid;
    if (tot<cnt)l=mid;
  }
  /*printf("%.9lf %.9lf\n",(double)((ans-mid*cnt)-cir),(double)ans);
  printf("%.6lf %.18lf\n",(double)cir,(double)mid);
  printf("%d %d\n",tot,cnt);*/
  // 查看初始WQS 

  if (cir+mid>eps){//可以选出k个整圆,则扰动无效
    flag=0;//开始扰动 
    while(tot!=cnt)adjust();
  }//else printf("       Error  %.9lf",(double)(cir*(cnt-1)));
  ans=0;cnt--;
  for (int i=cnt,tp=p[n];i;i--,tp=p[tp])st[i]=tp;
  return cir+mid>eps;
}
void sol(int l,int r,int tl,int tr,db *f,int *p)
{
  int mid=(l+r)>>1;
  f[mid]=0;p[mid]=tl;
  for (int i=tl;i<=min(tr,mid-1);i++){
    db sav=c(mid,i);
    if (sav>f[mid]){
      f[mid]=sav;p[mid]=i;
    }
  }
  if (l<mid)sol(l,mid-1,tl,p[mid],f,p);
  if (mid<r)sol(mid+1,r,p[mid],tr,f,p);  
}
db ff[2][MaxN];
int pp[2][MaxN];
void calc(int bp,int *l,int *r,int *sp)
{
  f[bp]=cir;
  if (bp==1&&r[cnt]==n+1)r[cnt]--;
  /*for (int i=2;i<=cnt;i++)
    printf("  [%d,%d]\n",l[i],r[i]);*/
  //查看决策区间
  sol(l[2],r[2],bp,bp,ff[0],pp[0]);
  for (int i=l[2];i<=r[2];i++)f[i]=ff[0][i];
  for (int i=3;i<=cnt;i++){
    sol(l[i],r[i],l[i-1],r[i-1],ff[i&1],pp[i&1]);
    for (int j=l[i];j<=r[i];j++)f[j]=ff[i&1][j];
  }
  int tp;x[n+2]=L+x[bp];
  db ret=0;
  for (int i=l[cnt];i<=r[cnt];i++){
    db sav=c(n+2,i);
    if (sav>ret){ret=sav;tp=i;}
  }
  ret-=cir;
  for (int i=cnt;i;i--){
    sp[i]=tp;
    tp=pp[i&1][tp];
  }
  /*for (int i=1;i<=cnt;i++){
    printf("%d ",sp[i]);
    //if (sp[i]<=sp[i-1])puts("!");
  }puts("");
  printf("  %d %.9lf\n",bp,(double)ret);*/

  if (ret+eps>ans){
    ans=ret;
    for (int i=1;i<=cnt;i++)
      st[i]=sp[i];
  }if (bp==1&&r[cnt]==n)r[cnt]++;
}
int sl[MaxN<<1],sr[MaxN<<1],sp[MaxN<<1];
void solve(int *l,int *r,int *sp)
{
  if (l[1]>r[1])return ;
  //printf("Solve [%d,%d]\n",l[1],r[1]);
  int mid=(l[1]+r[1])>>1,*tl=l+cnt+1,*tr=r+cnt+1,*tp=sp+cnt+1;
  calc(mid,l,r,sp);
  tl[1]=l[1];tr[1]=mid-1;
  for (int i=2;i<=cnt;i++)
    {tl[i]=l[i];tr[i]=sp[i];}
  solve(tl,tr,tp);
  tl[1]=mid+1;tr[1]=r[1];
  for (int i=2;i<=cnt;i++)
    {tl[i]=sp[i];tr[i]=r[i];}
  solve(tl,tr,tp);
}
int getall()
{
  int ml=1<<30,pos=0,sav=1;n--;
  for (int i=1;i<cnt;i++)
    if (st[i+1]-st[i]<ml){
      ml=st[i+1]-st[i];
      pos=i;
    }//寻找最短的一段并位移
  //for (int i=1;i<=cnt;i++)printf("%d ",st[i]);puts("");
  ml=x[st[pos]];
  for (int i=1;i<=n;i++)x[i]=(x[i]-ml+L)%L;
  sav=ml=st[pos];
  for (int i=1;i<=cnt;i++)st[i]=(st[i]-ml+n)%n+1;
  sort(st+1,st+cnt+1);sort(x+1,x+n+1);
  x[st[cnt+1]=n+1]=x[1]+L;
  for (int i=1;i<=cnt;i++){ 
    sl[i]=st[i];sr[i]=st[i+1];
    //注意保留端点
  }solve(sl,sr,sp);
  return sav;
}
int main()
{
  n=read();cnt=read();R=read();L=read();
  cir=Pi*R*R;eps=1e-10*sqrt(R);
  for (int i=1;i<=R+R;i++){
    tl[i]=acos(0.5*i/R)*2*R;
    ts[i]=(Pi-acos(0.5*i/R)*2)*R*R+sqrt(R*R-i*i*0.25)*i;
  }x[0]=-1000000;
  for (int i=1;i<=n;i++)
    x[i]=read();
  x[++n]=L+x[1];cnt++;
  int sav=1;
  if (getone())sav=getall();
  for (int i=1;i<=cnt;i++)st[i]=(st[i]+sav-2)%n+1;
  sort(st+1,st+cnt+1);
  for (int i=1;i<=cnt;i++)printf("%d ",st[i]);
  return 0;
}