自动搬运

查看原文

来自洛谷，原作者为

	沉石鱼惊旋 已完成今日我对着铁质的凳子踢了五下然后把那堆钢栏杆在地上滚了一下然后把椅子夹在了篮筐上大学习

搬运于2025-08-24 22:20:55，当前版本为作者最后更新于2024-04-02 16:39:02，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目思路

原来这种多边形转成笛卡尔树建树是常见 trick。练的太少导致的。

但是这题其实不用笛卡尔树建树，因为 DP 部分复杂度较高其实这个优化（至少在我的程序上）没有太大作用。

---

为了方便描述，定义中国象棋中的『車』为题目中的颜色，本质一样。

考虑把这个多边形转成树，分割方式就是以底层开割。

机房电脑的 NOI Linux 2.0 没有好用的画图软件，这里用一张别人题解的图。

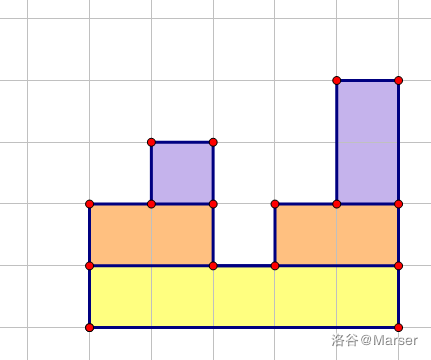
我们找到最低点，分成左右两边，分治建树。把最低端想象成子树的根，向上的一层不同颜色既是子节点。

如果不能分成恰好两棵子树，其实没有影响，把某两个放到一起先当成一个节点下一次分开来就好了，没有必要特别判这个问题。

然后这个问题被我们抽象成了树上问题，直接采取树形 DP 解决。

---

这里再提一个东西：

大小为 $n\times m$ 的棋盘，放入 $k$ 个『車』，互不攻击的方案数是 $\binom{n}{k}\times \binom{m}{k}\times k!$。

考虑选择 $k$ 行再选择 $k$ 列，方案数是 $\binom{n}{k}\times \binom{m}{k}$。因为列可以任意排列之后和行拼在一起成为不同的方案，所以还要乘上全排列方案数 $k!$。

---

回归本题，设计 $F_{u,i}$ 表示以 $u$ 为根的子树，放了 $i$ 个『車』的方案数。

但是直接乱转移复杂度有点烂，所以先处理 $G_{u,i}$ 表示以 $u$ 为根的子树，不包括矩形 $u$，也就是只考虑以 $u$ 的子节点为根的子树，放了 $i$ 个『車』的方案数。

$G$ 数组的转移是显然的，枚举两边分别放了几个。

以下定义 $ls$ 和 $rs$ 表示 $u$ 的左右子树根节点编号。

$$G_{u,i}\gets \sum\limits_{j=0}^{i} F_{ls,j} \times F_{rs,i-j},\forall i\in[1,k] $$

有了这个 $G$ 我们的 $F$ 就可以很快乐的转移了。枚举不包括自己的子树部分，放了几个，然后乘上自己选择的方案数。

但是，因为矩形之间联通，你需要处理有几列被子树部分的『車』覆盖的情况。直接把这几个位置扔掉就行了，剩下的同上面所说的方案数。

因此，$F$ 的转移呼之欲出。定义 $H_u,W_u$ 表示矩形 $u$ 的高和宽。

$$F_{u,i}\gets \sum\limits_{j=0}^{i} \binom {H_u}{i-j}\times \binom {W_u-j}{i-j}\times(i-j)! \times G_{u,j},\forall i\in[1,k] $$

总复杂度为 $\mathcal O(nk^2+n^2)$。

部分代码

洛谷 record 154003111

const int N = 1e6;
Z fac[N + 20];
Z inv[N + 20];
Z C(int n, int i) { return n < 0 || i < 0 || n < i ? 0 : fac[n] * inv[i] * inv[n - i]; }
#define ls c[u][0]
#define rs c[u][1]
int n, k;
int h[520];
int H[520];
int W[520];
int c[520][2];
Z f[520][520];
Z g[520][520];
int rt;
int build(int l, int r)
{
    if (l > r)
        return 0;
    int u = min_element(h + l, h + r + 1) - h;
    ls = build(l, u - 1);
    rs = build(u + 1, r);
    H[ls] = h[ls] - h[u];
    H[rs] = h[rs] - h[u];
    W[u] = r - l + 1;
    return u;
}
void dfs(int u)
{
    f[u][0] = g[u][0] = 1;
    if (!u)
        return;
    dfs(ls), dfs(rs);
    for (int i = 1; i <= k; i++)
        for (int j = 0; j <= i; j++)
            g[u][i] += f[ls][j] * f[rs][i - j];
    for (int i = 1; i <= k; i++)
        for (int j = 0; j <= i; j++)
            f[u][i] += C(H[u], i - j) * C(W[u] - j, i - j) * fac[i - j] * g[u][j];
}
int main()
{
    fac[0] = 1;
    for (int i = 1; i <= N; i++)
        fac[i] = fac[i - 1] * i;
    inv[N] = fac[N].pow(PPP - 2);
    for (int i = N; i >= 1; i--)
        inv[i - 1] = inv[i] * i;
    read(n, k);
    for (int i = 1; i <= n; i++)
        read(h[i]);
    rt = build(1, n);
    H[rt] = h[rt];
    dfs(rt);
    cout << f[rt][k] << endl;
    return 0;
}