自动搬运

查看原文

来自洛谷，原作者为

	DarkClever "Gallop on, Rocinante! Justice shall prevail!"

搬运于2025-08-24 22:20:43，当前版本为作者最后更新于2024-11-26 21:44:11，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

一道很好玩的题。

朴素做法是对于每个点，按照 $f_{i,j}$ 排序，之后用转移式 $\text{dp}_i = \max\{\text{dp}_j\} + 1$，

其中 $j$ 满足 $ (\lvert x_i - x_j\rvert = 1 \land \lvert y_i - y_j\rvert > 1) \lor (\lvert y_i - y_j\rvert = 1 \land \lvert x_i - x_j\rvert > 1)$。

显然，这样子遍历一整个矩阵的复杂度是 $O(n^4)$ 的，完全不可接受，考虑将其优化。

初步分析 $j$ 的限制，发现它只会在自己旁边竖条和上下的横条出现，即：

所以说，我们可以只遍历这 $4$ 段，寻找最大值，这样子的复杂度是 $O(n^3)$，还是不行。

这时，我们考虑到对于每一条，$\lvert x_i - x_j\rvert > 1$ 或 $\lvert y_i - y_j\rvert > 1$ 的限制至多会将一个段分为两个小段，所以我们考虑使用线段树等数据结构进行优化，理论可过，然后你就会空间爆掉并且发现这道题有着不同寻常的空间限制 $\leq 35\text{MB}$，而我们对每一条都需要开一颗线段树，总共要开 $2n$ 颗线段树，空间复杂度为 $O(n^2)$ 并且常数巨大，这时我们继续观察他的性质。

此时考虑在每一段中不满足 $\lvert x_i - x_j\rvert > 1$ 或 $\lvert y_i - y_j\rvert > 1$ 这个限制的点的数量，如图：

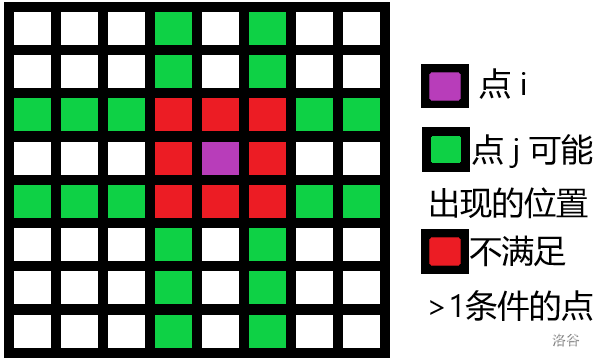
会发现每一段，不满足这个限制的点最多只有 $3$ 个，所以对于每一段，我们只需要维护前 $4$ 大的值即可，这样做的话时间复杂度为 $O(n^2)$，加上 $O(n^2\log n^2)$ 这个按 $f_{i,j}$ 排序的复杂度，总复杂度为 $O(n^2\log n^2)$，当然，如果使用基数排序，可以优化至 $O(n^2)$。

还有一点，注意到 $f_j > f_i$ 而非 $f_j \geq f_i$，所以在算完一个点的答案后，不能直接插入前 $4$ 大的数，应该等相同值的其他数全部处理完再一起插入。

#include <bits/stdc++.h>
using namespace std;
const int N = 1510;
struct node{
    short x,y;
    int val;
    int ans;
}a[N*N];
int n,cnt = 0,r1,c1;
bool cmp(node x,node y){
    return x.val < y.val;
}
void ins(node s[],node num){
    for(int i=1;i<=4;i++){
        if(s[i].ans<num.ans || (s[i].x==0 && s[i].y==0)){
            for(int j=4;j>i;j--){
                s[j] = s[j-1];
            }
            s[i] = num;
            return;
        }
    }
    return;
}
int query(int x,int y,node l[]){
    int maxn = 0;
    for(int i=1;i<=4;i++){
        if(((abs(l[i].x - x) == 1 && abs(l[i].y - y) > 1) || (abs(l[i].y - y) == 1 && abs(l[i].x - x) > 1)) && l[i].x!=0 && l[i].y!=0){
            //cerr<<x<<" "<<y<<" "<<l[i].x<<" "<<l[i].y<<'\n';
            maxn = max(maxn,l[i].ans);
        }
    }
    return maxn;
}
node l[N][5];
node r[N][5];
queue<node> q;
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    //cerr.tie(0);
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < 5; j++) {
            l[i][j].ans = 0;
            r[i][j].ans = 0;
        }
    }
    cin>>n>>r1>>c1;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            int x;
            cin>>x;
            a[++cnt].val = x;
            a[cnt].x = i;
            a[cnt].y = j;
            if(i == r1 && j == c1){
                
                a[cnt].ans = 1;
            }
        }
    }
    sort(a+1,a+cnt+1,cmp);
    int ans = 1;
    int lst = -1;
    for(int i=1;i<=cnt;i++){
        if(a[i].val!=lst){
            for(int j=i-1;j>=0 && a[j].val==lst;j--){
                ins(l[a[j].x],a[j]);
                ins(r[a[j].y],a[j]);
            }
        }
        lst = a[i].val;
        //cerr<<i<<" "<<a[i].x<<" "<<a[i].y<<" "<<a[i].val<<'\n';
        int maxn = a[i].ans;
        maxn = max(query(a[i].x,a[i].y,l[a[i].x-1]),maxn);
        maxn = max(query(a[i].x,a[i].y,l[a[i].x+1]),maxn);
        maxn = max(query(a[i].x,a[i].y,r[a[i].y-1]),maxn);
        maxn = max(query(a[i].x,a[i].y,r[a[i].y+1]),maxn);
        a[i].ans = maxn>0 ? maxn + 1 : 0;
        ans = max(ans,a[i].ans);
        //cerr<<a[i].ans<<'\n';
    }
    cout<<ans-1<<'\n';
	return 0;
}