[COCI 2014/2015 #2] BOB

0
15011418730 LV 7 @ 2025-8-24 22:20:28
自动搬运

查看原文

来自洛谷，原作者为

Kevin_Wa
ひさひとしんのう

搬运于2025-08-24 22:20:28，当前版本为作者最后更新于2020-10-25 21:20:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

本题作者思考很久，感受颇深。认为比较有价值，故写题解尽量详细。

题目大意

给你一个矩阵，问你这个矩阵所包含的所有每个元素相等的子矩阵的个数。

20pts

非常显然，使用 $O(n^4)$ 的 $dp$ 。开一个四维数组 $w[x1][y1][x2][y2]$ 来记录以 $(x1,y1)$ 为左上角， $(x2,y2)$ 为右上角的这个矩形是否满足每个元素都相等。

转移方程为：

$w[i][j][x][y]=w[i][j][x-1][y]$ & $w[i][j][x][y-1]$ & $(a[i][j]==a[x][y])$

具体代码如下：
```
#include<bits/stdc++.h>
using namespace std;
int a[1010][1010];
int n,m,ans;
bool w[51][51][51][51];
template <typename T> void read(T &x) {
x = 0; char c = getchar();int f=1;
for (; !isdigit(c); c = getchar())if (c=='-') f=-1;
for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
x*=f;
}
int main()
{
read(n);read(m);
for (int i=1;i<=n;i++)
  for (int j=1;j<=m;j++)
    read(a[i][j]);
if (n<=50 && m<=50)
  {
  	for (int i=1;i<=n;i++)
  	  for (int j=1;j<=m;j++)
  	    {
  	    w[i][j][i][j]=true;
  	    for (int x=0;x<i;x++)
  	      for (int y=0;y<=m;y++)
  	        w[i][j][x][y]=true;
  	    for (int x=0;x<=n;x++)
  	      for (int y=0;y<j;y++)
  	        w[i][j][x][y]=true;
  	    for (int x=i;x<=n;x++)
  	      for (int y=j;y<=m;y++)
  	        if (w[i][j][x-1][y] && w[i][j][x][y-1] && (a[i][j]==a[x][y])) w[i][j][x][y]=true;
  	    }
  	ans=0;
  	for (int i=1;i<=n;i++)
  	  for (int j=1;j<=m;j++)
  	    for (int x=i;x<=n;x++)
  	      for (int y=j;y<=m;y++)
  	        if (w[i][j][x][y]) ans++;
  	printf("%d\n",ans);
  	return 0;
  }

return 0;
}
```
理论上为60pts

$n^4$ 的复杂度对于这题是远远不够的，接下来我们先介绍我们要借助的两个数组。

$up$ 数组： $up[i][j]$ 表示 $a[i][j]$ 向上最多连续有几个点和 $a[i][j]$ 的数值相等。

$l$ 数组： $l[i][j]$ 表示 $a[i][j]$ 向左最多连续有几个点和 $a[i][j]$ 的数值相等。

接下来我们只要暴力枚举每个矩形的右下角的坐标，然后向上搜索，将整个与当前坐标的数值相等的这块东西扫描出来。

来张图思考一下。

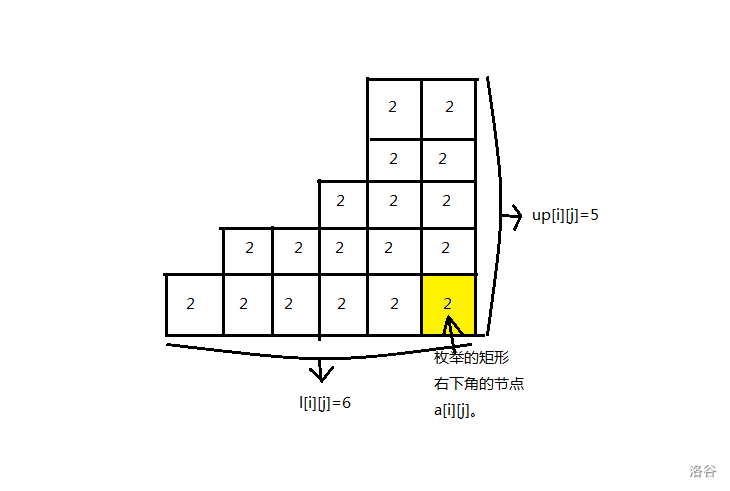
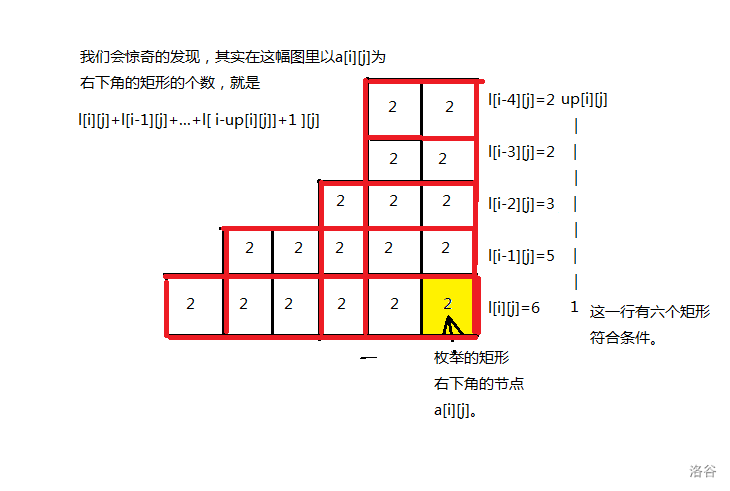
但是这只是严格单调递减时候的情况，在实际上遇到的情况远远不会这么简单。

假如我们遇到了这个图：

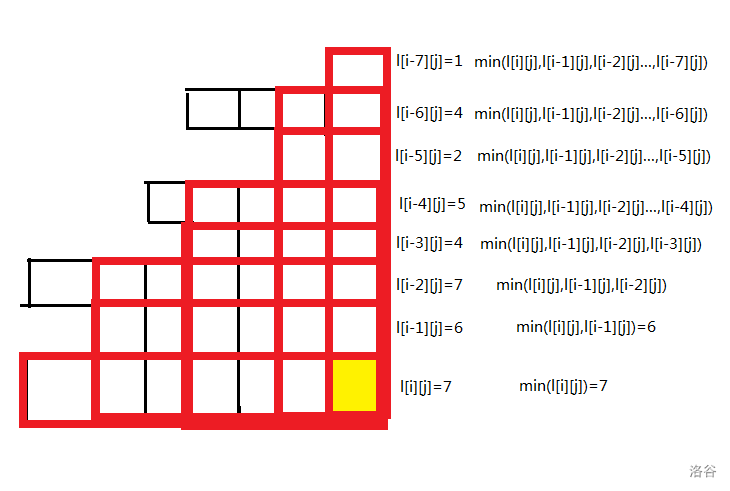
我们又一次很容易的发现，他只计算单调递减的部分。中途突出来的无法成为一个更大的矩形。

故我们向上扫描整个图形时，便可以顺带将 $l[k][j]$ 的最小值记录一下 ( $k=i->(i-up[i][j]+1)$ )，而这个最小值便是该行和该右下角贡献的答案。

代码：
```
#include<bits/stdc++.h>
using namespace std;
int a[1010][1010],l[1010][1010],up[1010][1010];
int n,m,sum;
long long ans;
template <typename T> void read(T &x) {
x = 0; char c = getchar();int f=1;
for (; !isdigit(c); c = getchar())if (c=='-') f=-1;
for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
x*=f;
}
int main()
{
//freopen("bob.in","r",stdin);
//freopen("bob.out","w",stdout);
read(n);read(m);
for (int i=1;i<=n;i++)
  for (int j=1;j<=m;j++)
    {
      read(a[i][j]);
      if (a[i][j]==a[i-1][j]) up[i][j]=up[i-1][j]+1;
      else up[i][j]=1;
      if (a[i][j]==a[i][j-1]) l[i][j]=l[i][j-1]+1;
      else l[i][j]=1;
	}
sum=0;
ans=0;
for (register int j=1;j<=m;j++)
  for (register int i=1;i<=n;i++)
    {
    	sum=l[i][j];
    	for (register int k=i;k>=i-up[i][j]+1;k--)
    	  {
    	  	if (sum>l[k][j]) sum=l[k][j];
    	  	ans+=sum;
		  }
	}
printf("%lld\n",ans);
return 0;
}
```
复杂度理论上是 $O(n^3)$ ，但是数据水+洛谷的评测姬跑的飞快。居然卡过去了。~~所以题解完结撒花（大雾）。~~

当然是不可能的。

真正的100pts

我们发现，其实只要我们先做纵坐标的递增，我们的所需的最小值答案是可以部分被上面传下来的，这样就可以优化掉扫描图形的时间。故我们运用单调栈维护这个东西。

因为我们需要的答案是单调递减的，所以我们我们维护栈内的元素单调递增，栈顶元素最大。若我们当前这个元素比栈顶元素大，那就把他放入栈顶。如果比栈顶小，那么我们将栈中元素弹出（将弹出元素的数量记录），直到找到比他小的栈顶，最后把他放入栈中，过程中统计答案。（栈中除了要存储当前元素值以外，还有存储当前元素值相同的个数）

依旧举这个例子。

这是单调栈内的情况。

num指当前元素值，v指元素个数。

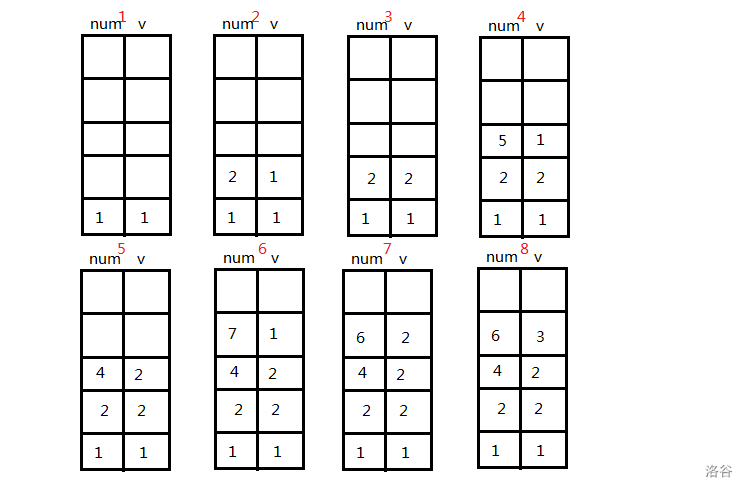
搞清了之后我们就可以看代码帮助理解了。

$Code:$
```
#include<bits/stdc++.h>
using namespace std;
struct node{
	int num,v;
}q[1010];
int a[1010][1010],l[1010][1010],up[1010][1010];
int n,m,sum,h,x;
long long ans;
template <typename T> void read(T &x) {
x = 0; char c = getchar();int f=1;
for (; !isdigit(c); c = getchar())if (c=='-') f=-1;
for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
x*=f;
}
int main()
{
//freopen("bob.in","r",stdin);
//freopen("bob.out","w",stdout);
read(n);read(m);
for (register int i=1;i<=n;i++)
  for (register int j=1;j<=m;j++)
    {
      read(a[i][j]);
      if (a[i][j]==a[i-1][j]) up[i][j]=up[i-1][j]+1;
      else up[i][j]=1;
      if (a[i][j]==a[i][j-1]) l[i][j]=l[i][j-1]+1;
      else l[i][j]=1;
	}
sum=0;
ans=0;
/*for (register int j=1;j<=m;j++)
  for (register int i=1;i<=n;i++)
    {
    	sum=l[i][j];
    	for (register int k=i;k>=i-up[i][j]+1;k--)
    	  {
    	  	if (sum>l[k][j]) sum=l[k][j];
    	  	ans+=sum;
		  }
	}*/
for (register int j=1;j<=m;j++)
  {
  	h=0;sum=0;
  	for (register int i=1;i<=n;i++)
  	  {
  	  	if (up[i][j]==1) h=0,sum=0;
  	  	x=l[i][j];
  	  	q[++h].num=x;
  	  	q[h].v=1;
  	  	sum+=x;
		while (h>1 && q[h-1].num>=q[h].num)
		  {
		  	h--;
		  	sum=sum-q[h].num*q[h].v-q[h+1].num*q[h+1].v;
		  	q[h].v+=q[h+1].v;
		  	q[h].num=q[h+1].num;
		  	sum=sum+q[h].num*q[h].v;
		  }
		ans+=sum;
		}
  }
printf("%lld\n",ans);
return 0;
}
```
此题区分度明显，部分分足。不失为一道好题。

撰写不易，望君满意。