自动搬运

查看原文

来自洛谷，原作者为

	szh_AK_all S挂分挂到被洛谷7级勾卡线|I can do all things

搬运于2025-08-24 22:20:25，当前版本为作者最后更新于2024-10-19 11:56:57，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

在打模拟赛时通过了这题，最终因这题而获得了第一名，写一篇题解纪念下。

分析

可以发现每个墙倒下之后，它所连接的两个数字间的最短路径变为了 $1$，可能对最终答案产生影响。所以很显然的一点是，我们可以记录一下所有的关键点，最后跑一遍最短路即可。

由于最短路不应该完全是由特殊路径（即倒下的墙）组成的，也就是说，对于两个关键点，我们还需要记录一条普通的边，假设这两个关键点是 $x,y$，那么这条边的权值便是 $|x-y|$。由于 $n$ 的范围很大，所以关键点应该离散化一下。

重点在于如何求关键点，也就是对于题目里给出的每个 $b$，我们需要求出其对应的 $a$。

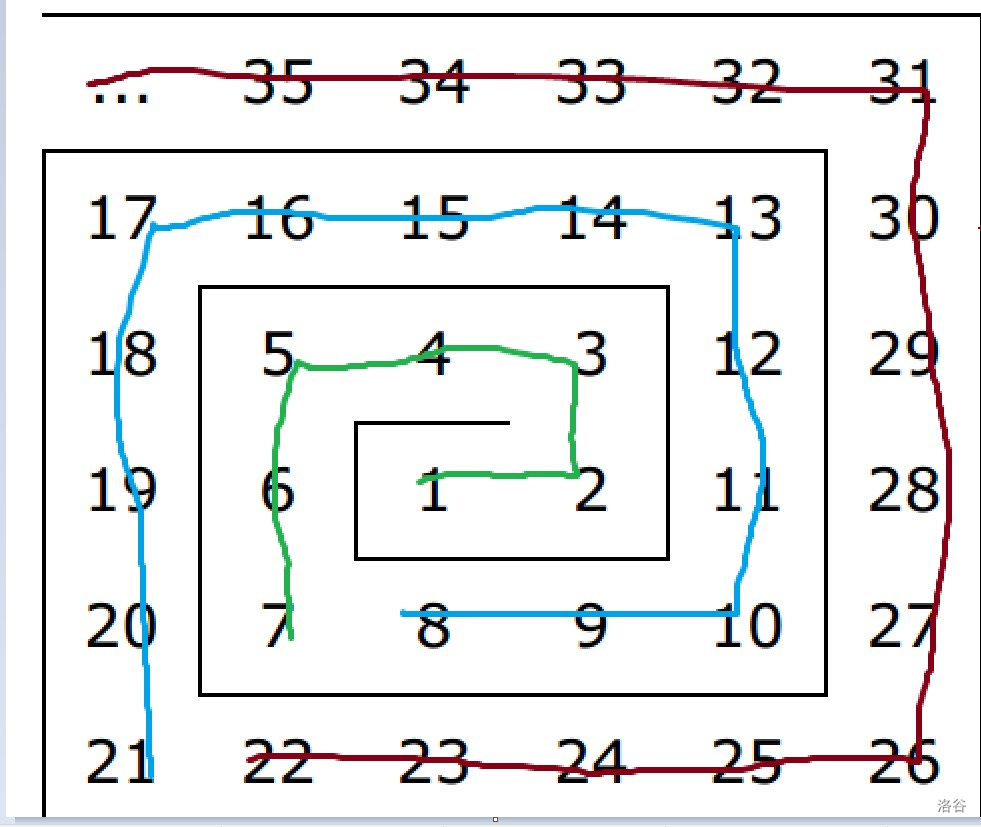
如上图所示，先将迷宫上的点一层层分类，绿色的点代表第一层，蓝色的点代表第二层，依此类推。那么对于一堵墙，它所关联的两个点应是在相邻的层里（除了 连接 $1,4$ 的这堵墙）。那么对于每一层，我们还应当将它分为上下左右四个块，从而按照块计算出对应点。

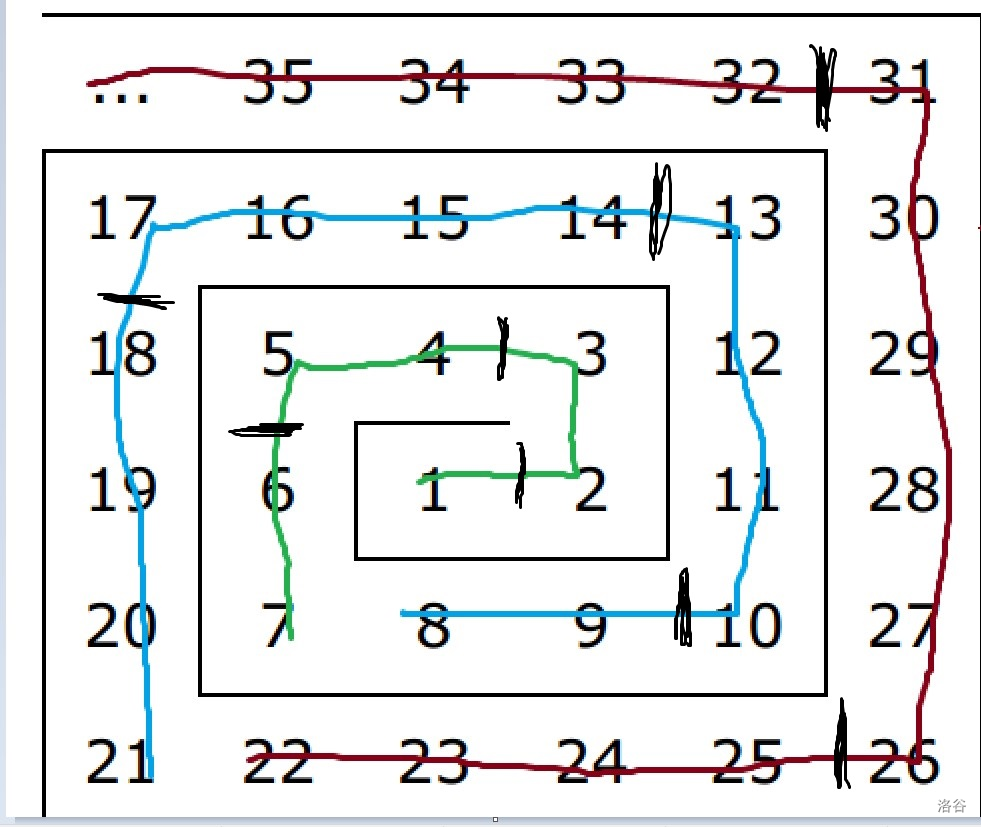
如图，用黑色的线将每一层割成四块，那么除开特殊的第一层，每一层下、右、上、左的块所包含的数量分别为 $(2,4,4,4),(4,6,6,6),(6,8,8,8)\dots$，用这样的方法计算，我们可以找出每一层每一块的最小数字（可视为“起点”），从而也可以算出每一层的最小数字和最大数字（即“起点”和“终点”）。

那么在算出当前点对对应的层及块后，它的对应点所在的层便应该是该层的上一层，所在的块应该是该块或者与该块相邻的分界点（因为两层对应块的大小不一样），从而算出对应点的数字号码。

Code

#include <bits/stdc++.h>
using namespace std;
#define int long long
int a[200005], tot, b[200005];

int xia(int x) {
	if (x == 1)
		return 1;
	if (x == 2)
		return 8;
	int la = 21 + 14 * (x - 3) + (x - 3) * (x - 2) / 2 * 8 + 1;
	return la;
}

int you(int x) {
	if (x == 1)
		return 2;
	if (x == 2)
		return 10;
	int la = 21 + 14 * (x - 3) + (x - 3) * (x - 2) / 2 * 8 + 1;
	return la + (x - 1) * 2;
}

int shang(int x) {
	if (x == 1)
		return 4;
	if (x == 2)
		return 14;
	int la = 21 + 14 * (x - 3) + (x - 3) * (x - 2) / 2 * 8 + 1;
	return la + (x - 1) * 2 + x * 2;
}

int zuo(int x) {
	if (x == 1)
		return 6;
	if (x == 2)
		return 18;
	int la = 21 + 14 * (x - 3) + (x - 3) * (x - 2) / 2 * 8 + 1;
	return la + (x - 1) * 2 + x * 2 + x * 2;
}

int get(int A) {
	int l = 1, r = 1000000000, ans = 0;
	while (l <= r) {//二分计算所在层
		int mid = (l + r) / 2;
		int la, now;
		if (mid == 1)
			la = 1, now = 7;
		else if (mid == 2)
			la = 8, now = 21;
		else
			la = 21 + 14 * (mid - 3) + (mid - 3) * (mid - 2) / 2 * 8 + 1, now = 21 + 14 * (mid - 2) + (mid - 2) * (mid - 1) / 2 * 8;
		if (la <= A && A <= now) {
			ans = mid;
			break;
		}
		if (la > A)
			r = mid - 1;
		else
			l = mid + 1;
	}
	if (ans == 1)//第一层第二层要特判
		return 1;
	if (ans == 2) {
		if (A >= 8 && A <= 9)
			return A - 7;
		if (A >= 11 && A <= 12)
			return A - 9;
		if (A >= 14 && A <= 16)
			return A - 11;
		return A - 13;
	}
	if (A < you(ans))//块
		return A - xia(ans) - 1 + xia(ans - 1);
	if (A < shang(ans))
		return A - you(ans) - 1 + you(ans - 1);
	if (A < zuo(ans))
		return A - shang(ans) - 1 + shang(ans - 1);
	return A - zuo(ans) - 1 + zuo(ans - 1);
}
vector<int>g[200005], w[200005];

struct node {
	int x, dis;
	friend bool operator<(node l, node r) {
		return l.dis > r.dis;
	}
	node(int aa = 0, int bb = 0) {
		x = aa;
		dis = bb;
	}
};
int vis[200005], dis[200005];

void dij() {
	for (int i = 2; i <= tot; i++)
		dis[i] = 10000000000000000;
	priority_queue<node>q;
	q.push(node(1, 0));
	while (!q.empty()) {
		int x = q.top().x;
		q.pop();
		if (vis[x])
			continue;
		vis[x] = 1;
		for (int i = 0; i < (int)g[x].size(); i++) {
			int y = g[x][i], ww = w[x][i];
			if (dis[x] + ww < dis[y]) {
				dis[y] = dis[x] + ww;
				q.push(node(y, dis[y]));
			}
		}
	}
}

signed main() {
	//reopen("maze.in", "r", stdin);
	//freopen("maze.out", "w", stdout);
	int n, m;
	cin >> n >> m;
	a[++tot] = 1, a[++tot] = n;
	b[1] = 1, b[2] = n;
	for (int i = 1; i <= m; i++) {
		cin >> a[++tot];
		b[tot] = a[tot];
		a[tot + 1] = get(a[tot]);
		tot++;
		b[tot] = a[tot];
		//cout << a[tot - 1] << " " << a[tot] << endl;
	}
	sort(b + 1, b + tot + 1);//离散化
	int nn = unique(b + 1, b + tot + 1) - (b + 1);
	for (int i = 1; i <= tot; i++)
		a[i] = lower_bound(b + 1, b + nn + 1, a[i]) - b;
	for (int i = 1; i <= m; i++) {//特殊边
		g[a[i * 2 + 2]].push_back(a[i * 2 + 1]);
		w[a[i * 2 + 2]].push_back(1);
		g[a[i * 2 + 1]].push_back(a[i * 2 + 2]);
		w[a[i * 2 + 1]].push_back(1);
	}
	for (int i = 1; i < nn; i++) {//普通边
		g[i].push_back(i + 1);
		w[i].push_back(b[i + 1] - b[i]);
		g[i + 1].push_back(i);
		w[i + 1].push_back(b[i + 1] - b[i]);
	}
	dij();
	for (int i = 1; i <= nn; i++) {
		if (b[i] == n) {
			cout << dis[i];
			return 0;
		}
	}
}

题解来之不易，看到最后记得点赞喵。