自动搬运

查看原文

来自洛谷，原作者为

	阴阳八卦 集天地之灵，成万物之美。

搬运于2025-08-24 22:20:14，当前版本为作者最后更新于2020-08-04 20:21:45，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

蒟蒻第一次写题解，多多包涵。感觉前面的大佬写得有点迷糊，对，就是我太菜了，蒟蒻来表达下自己的想法

对于本题而言，每个点有两种状态：选或不选。

同时题目又给出限制条件：点集内只能选一个点，一条边上至少选一个点

这也太明显了吧

所以就是在点集内，若选择某个点则另外的点不能选；一条边上，若不选某个点，则另一个点必选。此时已经很显然了，2-SAT建边跑强连通分量判断是否矛盾，完事

2-SAT板子过了才做这题的吧板子

但是如果直接暴力建边就会有这样的问题：记录

总有大数据会MLE或TLE！

而其根本原因就在与点集内的建边:

for(int i=1;i<=k;i++)
{
	scanf("%d",&t);
	for(int j=1;j<=t;j++)scanf("%d",&a[j]);
	for(int j=1;j<=t;j++)
	{
		for(int l=1;l<=t;l++)
     		if(l==j)continue;
		else add((a[j]-1)*2,(a[l]-1)*2+1);
	}
}

快乐超限

$N^2$的算法让人难以接受，时间空间过大，为解决这个问题必须优化点集内建边算法

这是我们原来的建图方式，朴素但是有效好歹92分

如何优化呢？关键就在于缩小$N^2$的计算量，而要完成这一步，关键是减少建边的数量（或者说优化建边的方式）

2-SAT里变量两种状态的点是关键，不可能直接在这$2N$个点之上优化。自然而然得，我们应当新建若干点作为媒介使新图拥有原来的性质，而这$2N$个点的地位等价（感觉一下？），自然应当新建$2N$个点一一对应（连边）

为保持原来点的性质不变，出点继续出，入点继续入

然后自然而然得，我们可以转移边

对于这幅图，我们容易发现没错非常容易，9-16，10-16，11-16这三条边可以变成9-10，10-11，11-16这样的三条边，而同时9-10还可以用于9-15，10-15到9-10，10-15的转换。所以经过这样的转化，我们能得到这张图

但是这张图存在致命的错误：出现了1-9-14-13-2，1-9-10-13-2之类的错误线路，为了调整这种线路，我们将9-14调整为9-4，10-13调整为3-13（保持9-10，14-13之类的由有利边仍然存在），类似操作后，有了这张图

此时图形已经符合原图的所有性质，但是为了便于进行循环操作，我们对其微调(也就4条边），得到这张图（也就是程序得到的图）

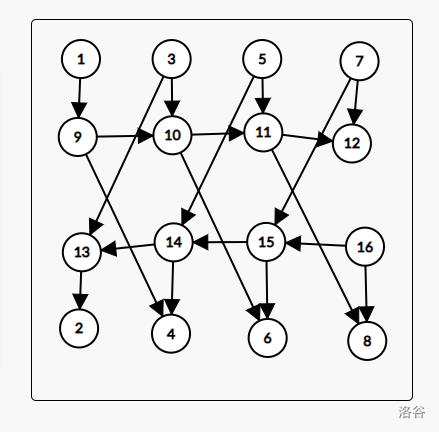
附上点集内代码，可以结合图片食用

int cntt=2*n;
for(int j=1;j<=k;j++)
{
	scanf("%d",&t);
	for(int i=1;i<=t;i++)
	{
		scanf("%d",&a[i]);
		pre[a[i]][0]=++cntt;//新建点
		pre[a[i]][1]=++cntt;//新建点
		add((a[i]-1)*2,pre[a[i]][0]);
		add(pre[a[i]][1],(a[i]-1)*2+1);
	}
	for(int i=2;i<=t;i++)
	{
		int d1=a[i-1],d2=a[i];
		add(pre[d1][0],pre[d2][0]);
		add(pre[d2][1],pre[d1][1]);
		add(pre[d1][0],(d2-1)*2+1);
		add((d2-1)*2,pre[d1][1]);
	}
}

最后附上AC代码

#include<bits/stdc++.h>
//(i-1)*2    (i-1)*2+1   
using namespace std;
const int N=2*1e6+10,M=2*1e7;
int dfn[2*N],low[2*N],fa[2*N],vis[2*N],st[2*N],head[2*N],a[N];
int to[2*M],Next[2*M],pre[N][2];
int cnt,p,cntk;
void add(int x,int y)
{
	to[cnt]=y;
	Next[cnt]=head[x];
	head[x]=cnt++;
}
void tar(int x)
{
	dfn[x]=low[x]=++cntk;
	vis[x]=1;
	st[++p]=x;
	for(int i=head[x];i!=-1;i=Next[i])
	{
		if(!dfn[to[i]])
		{
			tar(to[i]);
			low[x]=min(low[x],low[to[i]]);
		}
		else if(vis[to[i]])low[x]=min(low[x],dfn[to[i]]);
	}
	int cur;
	if(low[x]==dfn[x])
	{
		do{
			cur=st[p];
			p--;
			vis[cur]=0;
			fa[cur]=x;
		}while(cur!=x);
	}
}
void init()
{
	memset(head,-1,sizeof(head));
	cnt=0;
	cntk=0;
	p=0;
}
int main()
{
	init();
	int n,m,k,x,y,t;
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		add((x-1)*2+1,(y-1)*2);
		add((y-1)*2+1,(x-1)*2);
	}
	int cntt=2*n;
	for(int j=1;j<=k;j++)
	{
		scanf("%d",&t);
		for(int i=1;i<=t;i++)
		{
			scanf("%d",&a[i]);
			pre[a[i]][0]=++cntt;
			pre[a[i]][1]=++cntt;
			add((a[i]-1)*2,pre[a[i]][0]);//xuan ze lianchu
			add(pre[a[i]][1],(a[i]-1)*2+1);//lian dao bu xuan
		}
		for(int i=2;i<=t;i++)
		{
			int d1=a[i-1],d2=a[i];
			add(pre[d1][0],pre[d2][0]);
			add(pre[d2][1],pre[d1][1]);
			add(pre[d1][0],(d2-1)*2+1);
			add((d2-1)*2,pre[d1][1]);
		}
	}
	cntk=0;
	for(int i=0;i<=cntt;i++)
	if(!dfn[i])tar(i);
	bool flag=1;
	for(int i=1;i<=n&&flag;i++)
	if(fa[(i-1)*2]==fa[(i-1)*2+1])flag=0;
	if(flag) printf("TAK");
	else printf("NIE");
	return 0;
}