自动搬运

查看原文

来自洛谷，原作者为

	K0stlin LIFE IS A CIRCLE.

搬运于2025-08-24 22:20:11，当前版本为作者最后更新于2020-04-04 12:41:25，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

[St-OI Round 1] T3:树上询问 官方题解

原定时限是1.2s，本人std最慢的一个点是600ms，所以超1.2s的同学都要订正啊qwq。（不要喷我duliu！

废话不多说。

关于不随机数据：就是菊花树，是为卡掉枚举z出边的。

思路

这题乍一眼看上去好像并没有什么特别显而易见的做法（雾

但先画个图！

就以样例二为例：

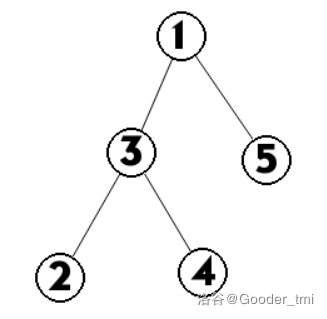
当我们找（2，5，z）的答案时，发现只有{2,3,1,5}可以作为LCA，因为他们在（2，5）的唯一路径上，所以发现z不在路径上时（比如4），就可以直接输0。

如果在路径上呢？

比如（2，5，3），3肯定是答案，然后我们把3给“拎”起来：

发现以4为根时，也可以。这时我们可以思考，是不是所有3的子节点都可以呢？

当然不是，2，5所在的子节点（即2，1）就不行，但其他子节点及其子节点下所有的节点都可以！（比如下图中的选中的所有节点）

思路明显了吧：当z在(x,y)路径上时，z和非路径上z的所有子节点（包括father）及其子孙节点就是答案！(如果纯看语言没看懂就看代码)

实现：

前置知识：

树上倍增（+求LCA），dfs序

首先一遍以1为根dfs求出dfs序和子树大小，再进行倍增预处理。

然后分4种情况讨论：

在路径上时：

1. $z$是$(x,y)$的LCA$=>$ $z->x$和$z->y$的子节点在路径上,去掉

2. $z$在$x->LCA$的路径上$=>$ $z->x$和$z->father(z)$的子节点在路径上,去掉

3. $z$在$LCA->y$的路径上$=>$ $z->y$和$z->father(z)$的子节点在路径上,去掉

不在路径上时：

4. print(0);

CODE:

#include <cstdio>
#define For(x) for(int i=hd[x];i;i=e[i].nxt)
#define v (e[i].to)
#define fsize(x) (n-size[x])//father子树大小
#define swp(x,y) (x^=y^=x^=y)
const int N=5e5+5;
int n,m,x,y,z,hd[N],num;
struct cz {
	int nxt,to;
}e[N<<1]; 
int size[N],tim[N],dep[N],cnt;//size是子树大小，tim是时间戳（dfs序），dep是节点深度
int lg[N],f[N][30];//倍增用
inline int read() {
	int x=0,flag=0;char ch=getchar();
	while(ch<'0'||ch>'9'){flag|=(ch=='-');ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return flag?-x:x;
}
inline void add(int x,int y) {
	e[++num]=(cz) {hd[x],y};
	hd[x]=num;
}
void dfs(int x,int father) {
	size[x]=1;tim[x]=++cnt;dep[x]=dep[father]+1;
	f[x][0]=father;
	For(x) {
		if(v==father) continue;
		dfs(v,x);
		size[x]+=size[v];
	}
}
inline int Lca(int x,int y) {
	if(dep[x]<dep[y]) swp(x,y);
	for(int i=lg[n];i>=0;--i)
		if(dep[f[x][i]]>=dep[y])
			x=f[x][i];
	if(x==y) return x;
	for(int i=lg[n];i>=0;--i)
		if(f[x][i]!=f[y][i])
			x=f[x][i],y=f[y][i];
	return f[x][0];
}
inline bool be_in(int x,int z) {return (tim[z]<=tim[x]&&tim[x]<=tim[z]+size[z]-1);}
//判断x在不在z的子树上
inline int tot(int x,int fa) {//x一直jump(倍增)到fa子节点的位置
	if(x==fa) return 0;
	for(int i=lg[n];i>=0;--i)
		if(tim[f[x][i]]>tim[fa])
			x=f[x][i];
	return size[x];
}
int main() {
	n=read();m=read();
	for(int i=2;i<=n;++i) lg[i]=lg[i-1]+(1<<(lg[i-1]+1)==i?1:0);
	for(int i=1;i<n;++i) {
		x=read();y=read();
		add(x,y);add(y,x);
	}
	dfs(1,0);
	for(int j=1;j<=lg[n];++j)
		for(int i=1;i<=n;++i)
			f[i][j]=f[f[i][j-1]][j-1];
	for(int i=1;i<=m;++i) {
		x=read();y=read();z=read();//下面就是4种情况
		if(Lca(x,y)==z) printf("%d\n",n-tot(x,z)-tot(y,z));
		else if(be_in(x,z)&&!be_in(y,z)) printf("%d\n",n-tot(x,z)-fsize(z));
		else if(be_in(y,z)&&!be_in(x,z)) printf("%d\n",n-tot(y,z)-fsize(z));
		else printf("0\n");
	}
	return 0;
}

-完-