自动搬运

查看原文

来自洛谷，原作者为

	Diu 上分！

搬运于2025-08-24 22:19:56，当前版本为作者最后更新于2021-10-19 21:14:15，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目传送门

线段树优化建图

我们可以从最朴素的思路开始想起。

0.0 暴力建图

对于一堆道路 $(a,b),(c,d)$，两两连边。

1.0 连向公共边

对于一堆道路 $(a,b),(c,d)$，我们让 $(a,b)$ 连向一个虚拟点 $k$，

再从 $k$ 向 $(c,d)$ 连边。

但是这样总共要连 $2nm$ 条边，肯定会炸。

所以要想办法优化连边的边数。

2.0 线段树优化建图

这个时候线段树重磅出击。

• 性质 2.1 对于一个区间的点 $(l,r)$，一个包含它的区间 $(L,R)$ 连向的点，那么 $(l,r)$ 也能连向。

• 性质 2.2 对于一个区间的点 $(l,r)$，另一个点 $a$ 如果能到达一个包含 $(l,r)$ 区间 $(L,R)$，那么点 $a$ 也能到达 $(l,r)$。

由此，我们便可建出两棵线段树，进树和出树。

同时，这也是为什么进树从父节点连向子节点，二出树从子节点连向父节点的原因。

不把两棵树建到一块，是为了防止直接顺着线段树直接走完所有点。

而对于一个区间 $(l,r)$ 它在进树、出树本质上是一个点。

所以经过某条边到达进树后，可以回到出树继续走下一条边。

也就是说进树的点直接连向对应的出树的点。

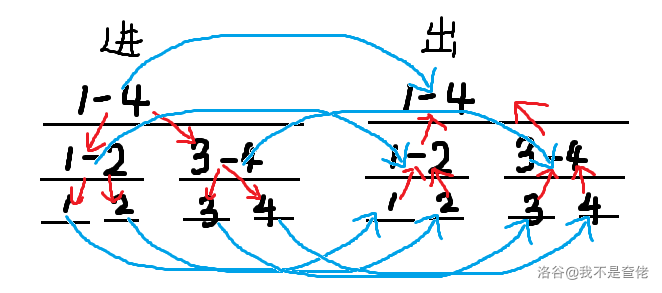
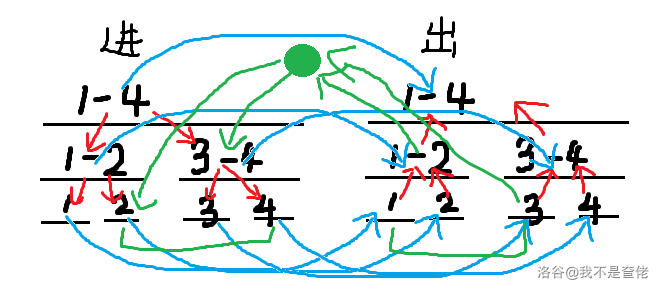
图中绿色的边权之标上 $1$，但是最后答案要除以 $2$。

因为从 $(a,b)$ 连到 $(c,d)$ 经过两条绿边，路程算了 $2$，但其实只用算一条，所以要除以 $2$。

或者连向绿点的边和绿点连出的边任意一个标权值也可以。

code

#include<bits/stdc++.h>
#define ls(o) (o<<1)
#define rs(o) (o<<1|1)
//#define int long long
using namespace std;
const int N=500010,M=4200010;
int n,m,p,out,num[N];
struct edge{
    int v,w;
};
vector<edge> g[M];
void build_in(int o,int l,int r){
    if(l==r)return;
    int mid=l+r>>1;
    build_in(ls(o),l,mid);
    build_in(rs(o),mid+1,r);
    g[o].push_back({ls(o),0});
    g[o].push_back({rs(o),0});
}
void build_out(int o,int l,int r){
    g[o].push_back({o+n*4,0});
    if(l==r)return (void)(num[l]=o+n*4);
    int mid=l+r>>1;
    build_out(ls(o),l,mid);
    build_out(rs(o),mid+1,r);
    g[ls(o)+n*4].push_back({o+n*4,0});
    g[rs(o)+n*4].push_back({o+n*4,0});
}
void merge1(int o,int l,int r,int x,int y,int k){
    if(l>=x&&r<=y)return (void)(g[k].push_back({o,1}),g[o+n*4].push_back({k+1,1}));
    int mid=l+r>>1;
    if(mid>=x)merge1(ls(o),l,mid,x,y,k);
    if(mid<y)merge1(rs(o),mid+1,r,x,y,k);
}
void merge2(int o,int l,int r,int x,int y,int k){
    if(l>=x&&r<=y)return (void)(g[k+1].push_back({o,1}),g[o+n*4].push_back({k,1}));
    int mid=l+r>>1;
    if(mid>=x)merge2(ls(o),l,mid,x,y,k);
    if(mid<y)merge2(rs(o),mid+1,r,x,y,k);
}
int d[M];
bool vis[M];
deque<int> q;
void dijstra(int s){
    memset(d,127,sizeof(d));
    d[s]=0;
    q.push_front(s);
    while(!q.empty()){
        int u=q.front();
        q.pop_front();
//      if(vis[u])continue;
//      vis[u]=1;
        for(int i=0;i<g[u].size();i++){
            int v=g[u][i].v;
//          if(vis[v])continue;
            int w=g[u][i].w;
            if(d[v]>d[u]+w){
                d[v]=d[u]+w;
                if(w==1)q.push_back(v);
                else q.push_front(v);
            }
        }
    }
}
inline char nc(){
    static char buf[1000010],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000010,stdin),p1==p2)?EOF:*p1++;
}
//#define nc getchar
inline int read(){
    register int s=0,w=0;
    static char ch=nc();
    for(;!isdigit(ch);)ch=nc();
    for(;isdigit(ch);){
        s=(s<<1)+(s<<3)+(ch^48);
        ch=nc();
    }
    return w?-s:s;
}
signed main(){
    n=read(),m=read(),p=read();
    build_in(1,1,n);
    build_out(1,1,n);
    for(register int a,b,c,d,i=1;i<=m;++i){
        a=read(),b=read(),c=read(),d=read();
        merge1(1,1,n,a,b,n*8+i*2);
        merge2(1,1,n,c,d,n*8+i*2);
    }
    dijstra(num[p]);
    for(register int i=1;i<=n;++i)printf("%d\n",d[num[i]]/2);
//  for(int i=1;i<=tot;i++){
//    printf("%lld %lld %lld %lld:\n",i,tr[i].l,tr[i].r,g[i].size());
//    for(int j=0;j<g[i].size();j++)printf("%lld %lld\n",g[i][j].v,g[i][j].w);
//  }
}