自动搬运

查看原文

来自洛谷，原作者为

	NDFS 半退谷

搬运于2025-08-24 22:19:51，当前版本为作者最后更新于2022-07-17 22:01:12，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

看了一下别人都写的是 $O(n^3)$ 的解法，这里提供一个 $O(n^2\log n)$ 的正解。

$O(n^3)$ 的解法基本上都是直接枚举三个点再根据勾股定理逆定理判断直角三角形，但下面的这种解法是根据斜率判断的。

首先枚举一个点，平移整个坐标系，使这个点落在原点上。具体地说，就是其他点的横纵坐标都分别减去这个点的横纵坐标。然后再判定直角。

现在我们需要找另外两个点与其构成直角三角形，设其为点 $A$ 和 点 $B$，则要使 $AO \perp BO$，所以这两个点一定在相邻的两个象限（正好落在坐标轴上的情况是类似的）。设 $A$、$B$ 分别在第一象限和第二象限（都是一样的证明方法），如图所示。

可以发现，当 $AO\perp BO$ 时：

$\because\angle AOB=90^{\circ}=\angle 2+\angle 3$

又 $\because\angle 1+\angle 3=90^{\circ}$

$\therefore\angle 1=\angle 2$

反过来，当 $\angle 1=\angle 2$ 时：

$\because\angle AOB=\angle 2+\angle 3$

又 $\because\angle 1=\angle 2$

$\therefore\angle AOB=\angle 1+\angle 3=90^{\circ}$

$\therefore AO\perp BO$

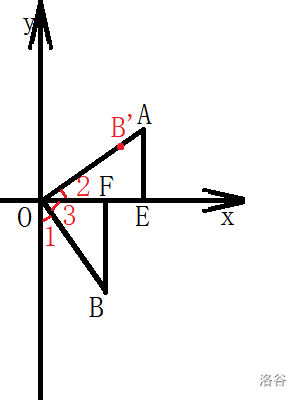
那要如何判断 $\angle 1=\angle 2$ 呢？将线段 $BO$ 绕点 $O$ 逆时针旋转 $90^{\circ}$ 得到 $OB'$，如果 $\angle 1=\angle 2$ 那么 $OB'$ 会与 $OA$ 重合，所以 $OB'$ 与 $OA$ 斜率相同。

所以解法流程：

1. 枚举作为原点的点，平移其他点，并旋转到第一象限。
2. 按照斜率排序，斜率相同的点都会连成一段。
3. 统计四个象限斜率相同的点，相邻象限点数相乘累加答案

总的时间复杂度 $O(n\times(n\log n+n))$，也就是 $O(n^2\log n)$，可能可以用基数/计数排序优化到 $O(n^2)$。

补充： 排序时要判断 $\frac{y_A}{x_A}$ 与 $\frac{y_B}{x_B}$ 的大小关系，可以交叉相乘，比较 $y_A\times x_B$ 与 $y_B\times x_A$。

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
struct point
{
	ll x,y;int k;//横纵坐标和象限
}p[1505];
int n,ans=0;
ll x[1505],y[1505];
void swap(int &a,int &b){a=a^b,b=a^b,a=a^b;}
void xz(int t)
{//我写了顺时针旋转，这样方便计算在第几象限，坐标关系可以手推出来
	p[t].k++,swap(p[t].x,p[t].y),p[t].y=-p[t].y;
}
bool cmp(point a,point b)
{//比较斜率，为了避免误差把除法通分换乘法
	return a.y*b.x<b.y*a.x;	
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%lld%lld",&x[i],&y[i]);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(j!=i)
			{
				p[j].x=x[j]-x[i],p[j].y=y[j]-y[i],p[j].k=1;
				while(p[j].x<=0||p[j].y<0)xz(j);//一直转到第一象限，可能在坐标轴上所以横坐标等于零也要转
			}
			else p[i]=p[1];//原点不能排序，因为不能除以零，会出问题
		}
		sort(p+2,p+1+n,cmp);
		for(int j=2,k;j<=n;j=k)//从上次结束的地方开始
		{
			int s[4]={0};//统计四个象限
			for(k=j;k<=n;s[p[k].k-1]++,k++)if(p[j].y*p[k].x!=p[k].y*p[j].x)break;//排序后相同的肯定时连续一段，不相同直接break
			for(int i=0;i<=3;i++)ans+=s[i]*s[(i+1)%4];
		}
	}
	printf("%d",ans);
	return 0;
}