自动搬运

查看原文

来自洛谷，原作者为

	xtx1092515503 Mathematics compares the most diverse phenomena, and discovers the secret analogies which unite them. @Joseph Fourier

搬运于2025-08-24 22:19:14，当前版本为作者最后更新于2020-05-21 17:17:17，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

（本题解部分借鉴于这里，但是自己加入了部分感性的理解）

神题。

考虑我们现在树上有$k$头牛。它们无论散布在树的什么地方，我们总可以移动某些牛，使得这$k$头牛位于树上的$1\dots k$号点。这是非常显然的。

---

我们考虑一下，假设位置$(x,y)$上的牛是可以在不改动其它位置上的牛的前提下完成交换的，我们把它称作“交换关系”（注意这一名词是针对位置的，不针对位置上到底是哪头牛）。则如果位置$(x,y)$与位置$(y,z)$都具有“交换关系”，那么，位置$(x,z)$也将具有交换关系，因为我们可以先交换位置$(x,y)$，再交换$(y,z)$，再交换$(x,y)$达到交换。换句话说，“交换关系”这种性质，具有可传递性。

则我们如果把“交换关系”看作边的话，它们将会构成许多团（完全图）。设这些团的大小为$s_i$，则有$k$头牛时的答案即为$\dfrac{k!}{\sum s_i!}$。

---

现在我们考虑一下，什么情况下两个位置$(x,y)$会具有“交换关系”。

我们不妨想一想，假如你正常地想调换两个位置，你会怎么做？

我们画出图来：

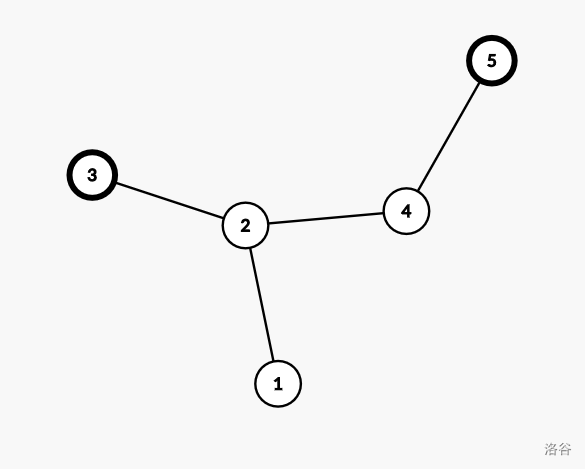
假设我们要交换位置$3$和$5$的牛，应该怎么办？

先把一头牛移到$1$等待，然后再移动另一头牛。

这启发我们在移动牛时需要在分叉的路径上等待。

也就是说，在一条直线上的牛是不可能交换的。只有有“分叉”的地方才能完成交换。

---

什么样的地方不存在“分叉”呢？

对，一条路径。

我们定义一条“链”为一条路径，使得路径两端的点的度数都不等于$2$，而链上其它点的度数都等于$2$。

典型的例子：

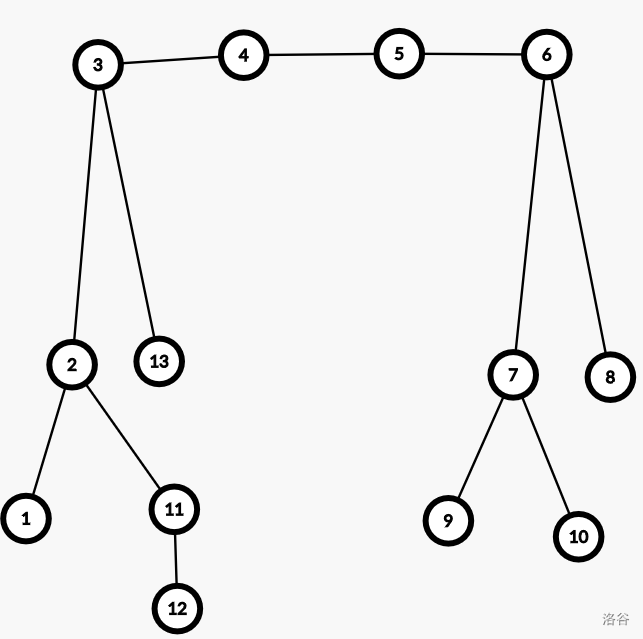
$(3-4-5-6)$是一条链，链的两端是子树$3$与子树$6$。（实际上，如$(2-11-12)$，$(7-9)$都是链）。

我们来看一下更抽象的草图：

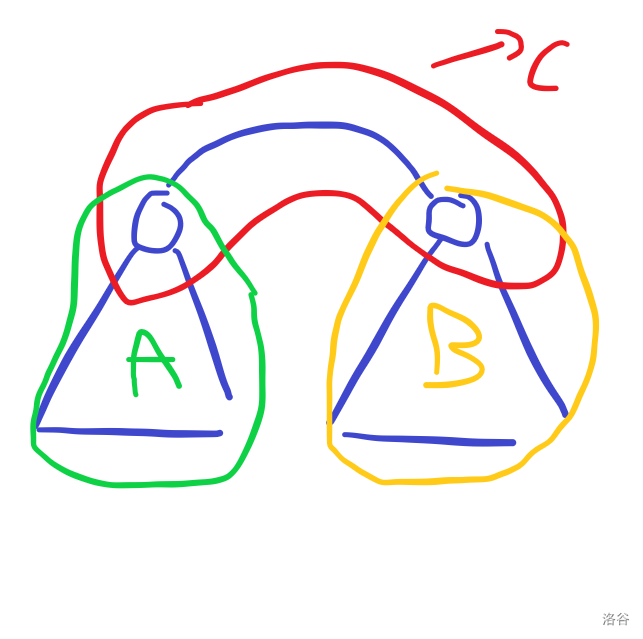
我们设左边子树有$\color{green}{A}$个点，右边子树有$\color{orange}{B}$个点，链上有$\color{red}{C}$个点（注意链两段的点既属于链，又属于子树）。

则如果$\color{red}k<(A-1)+(B-1)$的话，左右子树的点就可以任意交换。

我们感性理解一下：

首先，将所有$k$个点全都移到$A$子树或$B$子树中。则此时链上没有任何点（包括链两段），并且两颗子树中至少有一个空隙。

则这一个空隙，就可以成为我们之前提到的“等待”处，进行交换。

而只要能完成一次“交换”，则所有位置都可以交换。

（感性理解一下吧……严谨的证明我自己都看不懂……）

因为$(A-1)+(B-1)=N-C$，因此只要$k<N-C$，两边子树就是可交换的。

---

我们考虑删去所有满足上述要求的链上的边。如果从大到小地枚举$k$的话，则删边就会变成加边，就可以使用并查集维护联通块。

考虑对于一坨联通块，有多少个外部节点可以通到它。设$(a_i,b_i)$为一条链，使得链的一端在块内，一端在块外。再设$B_i$为该链通到的另一端的子树大小。

则能通到该联通块的节点数量为

$$k-\sum\limits_{(a_i,b_i)}(k-B_i-1)$$

（感性理解：外层用$k$减去的那一大坨，是通不到的点的数量；而内层用$k$减去的，则是对于当前链$(a_i,b_i)$来说，能通到联通块内的数量。很明显这样做可能会重复计算，但估计容斥容斥就出来了？）

---

我们对于每个联通块，维护它内部的边数量$ins$与它周围被切断的边数$out$。

则按照实际意义化简，我们得到了

$$k-(n-ins-1)+(n-k-1)out$$

理解：

$(n-ins-1)$是外部的点数量（注意$ins$是边数）。我们一开始假设这所有外部的点全部通不到）

$out$是被切断的边数，就是上述的$(a_i,b_i)$的数量。乘上$(n-k-1)$是子树中原本的$k$个点数量，再加上需要空出来的那个“等待区”的大小。这是$(n-ins-1)$中多减去的那些点。

再套上我们一开始得出的那个公式$\dfrac{k!}{\sum s_i!}$，则我们得出的那个$k-(n-ins-1)+(n-k-1)out$的式子就是分母中的$s_i$。通过预处理阶乘和阶乘的逆元，我们可以直接应用公式。

---

最后是统计答案。直接枚举每个联通块即可，不必担心复杂度，因为所有时刻的联通块数量是$O(n)$的（联通块数量与 $\sum\text{链长}$ 是同级别的）。

复杂度分析：瓶颈在于添加上符合要求的链时，为了方便在$k$递减时直接处理要排序。如果用桶排，复杂度就是$O(n)$的。这里为了图方便，使用的是$O(n\log n)$的常规排序。然后是并查集，复杂度是$n\alpha(n)$的。这里为了方便，没有按秩合并，因此仍然是$O(n\log n)$的。另一个瓶颈就是维护仍然存在的联通块标号，只能采取平衡树等在$O(n\log n)$内通过。但是我不小心敲的是vector，理论复杂度是$O(n^2)$的，会被菊花图卡掉，但是没有被卡，大家敲的时候用普通set即可。

#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
int ksm(int x,int y){
	int z=1;
	for(;y;x=1ll*x*x%mod,y>>=1)if(y&1)z=1ll*z*x%mod;
	return z;
}
int n,fac[100100],inv[100100],res[100100];
vector<int>g[100100],key;
struct dsu{
	int fa,ins,out;
}a[100100];
void init(){
	for(int i=1;i<=n;i++)if(g[i].size()!=2)a[i].fa=i,a[i].out=g[i].size(),key.push_back(i);
	fac[0]=1;
	for(int i=1;i<=n;i++)fac[i]=1ll*fac[i-1]*i%mod;
	inv[n]=ksm(fac[n],mod-2);
	for(int i=n-1;i>=0;i--)inv[i]=1ll*inv[i+1]*(i+1)%mod;
}
int find(int x){
	return a[x].fa==x?x:a[x].fa=find(a[x].fa);
}
void merge(int x,int y,int z){
	x=find(x),y=find(y);
	if(x==y)return;
	key.erase(lower_bound(key.begin(),key.end(),y));
	a[x].ins+=a[y].ins+z-1,a[x].out+=a[y].out-2,a[y].fa=x;
}
struct path{
	int x,y,z;
	path(int u,int v,int w){x=u,y=v,z=w;}
	friend bool operator <(const path &x,const path &y){
		return x.z<y.z;
	}
};
vector<path>paths;
void getpath(int x,int fa,int len,int from){
	if(g[x].size()!=2){
		if(from)paths.push_back(path(from,x,len));
		len=1,from=x;
	}
	for(auto y:g[x])if(y!=fa)getpath(y,x,len+1,from);
}
int main(){
	scanf("%d",&n);
	for(int i=1,x,y;i<n;i++)scanf("%d%d",&x,&y),g[x].push_back(y),g[y].push_back(x);
	init();
	getpath(key.front(),0,0,0);
	sort(paths.begin(),paths.end());
	for(int i=n-1,j=0;i;i--){
		while(j<paths.size()&&i<n-paths[j].z)merge(paths[j].x,paths[j].y,paths[j].z),j++;
		res[i]=fac[i];
		for(auto x:key)res[i]=1ll*res[i]*inv[i-(n-a[x].ins-1)+a[x].out*(n-i-1)]%mod;
	}
	res[n]=fac[n];
	for(int i=1;i<=n;i++)printf("%d\n",res[i]);
	return 0;
}

---

代码：