1 条题解
-
0
自动搬运
来自洛谷,原作者为

ez_lcw
**搬运于
2025-08-24 22:19:13,当前版本为作者最后更新于2020-05-16 11:31:39,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
先讲一下等会要用到的定义:
-
红格代表被甜玉米洒水器喷洒到的方格,蓝格代表被苜蓿洒水器喷洒到的方格。橙格代表有甜玉米洒水器的方格,紫格代表有苜蓿洒水器。
-
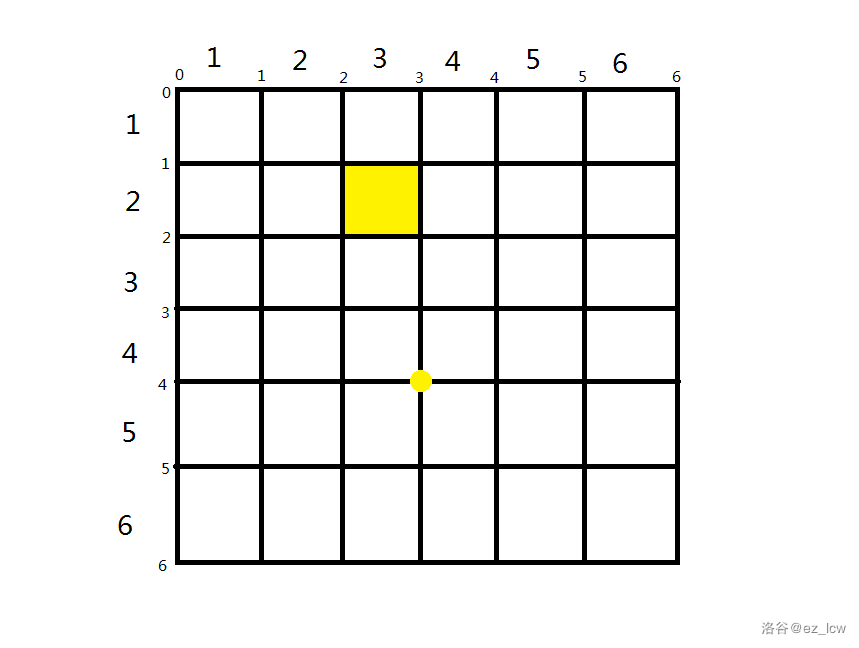
指网格线的交点, 指网格。
比如下面这个图中,黄点代表的是 ,黄格代表的是 。
-
表示网格图的第 行中有多少个没被占据的网格。
然后说说考试时的心路历程。(其实是用来帮助你如何由暴力思考到正解的)第一眼看到这道题是不会的……
甚至连部分分都不知道怎么写但是仔细想了一想,发现红蓝两方阵营肯定是被一条由 到 的分割线分开的。
比如说这样:
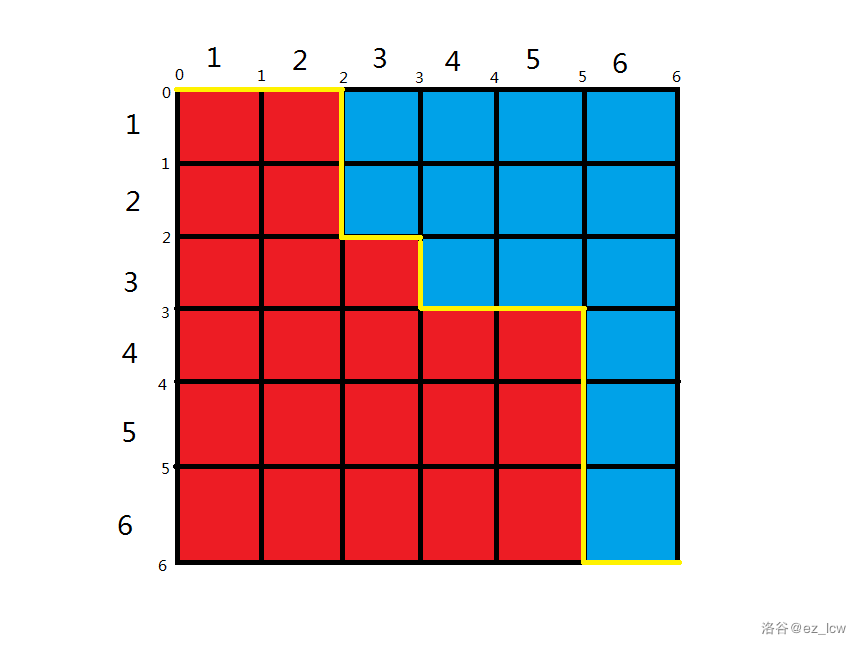
这种情况是被如图的黄色的分割线分开的。
然后考虑哪些地方需要洒水器:
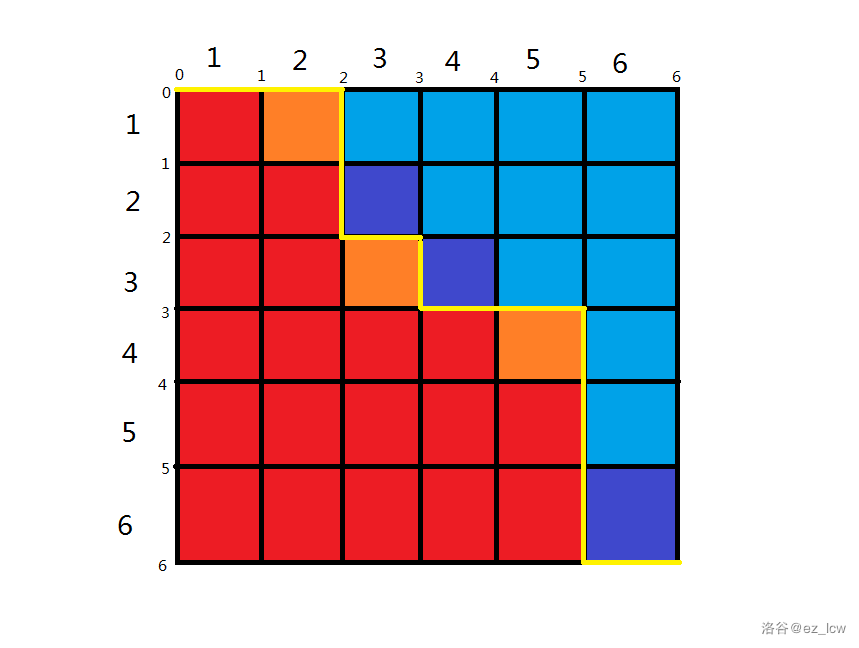
显然,我们发现,在分割线的拐角处都需要洒水器(即图中的橙格和紫格),其他地方可填可不填,但是只能填一种洒水器。
我们假设某一种分割线有 个拐角(也就是有 个洒水器是一定要放的),方阵总面积为 (面积指没有被占据的网格的总数)。
那么对于这种分割线,一共有 种方案。(记住这条公式)
那么暴力的方法就显而易见了:每次枚举一条分割线,并记录分割线的拐角数,最后统计答案。
时间复杂度貌似是 ,只有 。
代码:
#include<bits/stdc++.h> #define N 2010 #define mod 1000000007 using namespace std; int n,ans,poww[N*N],sum; char ch[N][N]; //n=4 // 0 1 2 3 4 //0######### // #.#.#W#.# //1######### // #.#.#W#W# //2######### // #W#W#.#.# //3######### // #.#.#.#W# //4######### //last=0向下,last=1向上 void dfs(const int x,const int y,const int a,const int b,const int last) { if(x==n&&y==n) { ans=(0ll+ans+1ll*poww[sum-a-b])%mod; return; } if(!last) { if(x+1<=n) dfs(x+1,y,a,b,0); if(y+1<=n&&ch[x][y+1]!='W') dfs(x,y+1,a,b+1,1); } else { if(x+1<=n&&ch[x+1][y]!='W') dfs(x+1,y,a+1,b,0); if(y+1<=n) dfs(x,y+1,a,b,1); } } inline int read() { int x=0; char ch=getchar(); while(ch<'0'||ch>'9') ch=getchar(); while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^'0'); ch=getchar(); } return x; } int main() { n=read(); poww[0]=1; for(register int i=1;i<=n*n;i++) poww[i]=(2ll*poww[i-1])%mod; for(register int i=1;i<=n;i++) scanf("%s",ch[i]+1); for(register int i=1;i<=n;i++) for(register int j=1;j<=n;j++) sum+=(ch[i][j]=='.'); dfs(1,0,0,0,0); dfs(0,1,0,0,1); printf("%d\n",ans); return 0; }考虑 ,设 指已经把前 行灌溉满了,分割线的终止在 ,分割线最后的方向是向右/向下的。
那么答案显然就是 。
考虑状态转移方程。
-
先考虑 怎么转移:
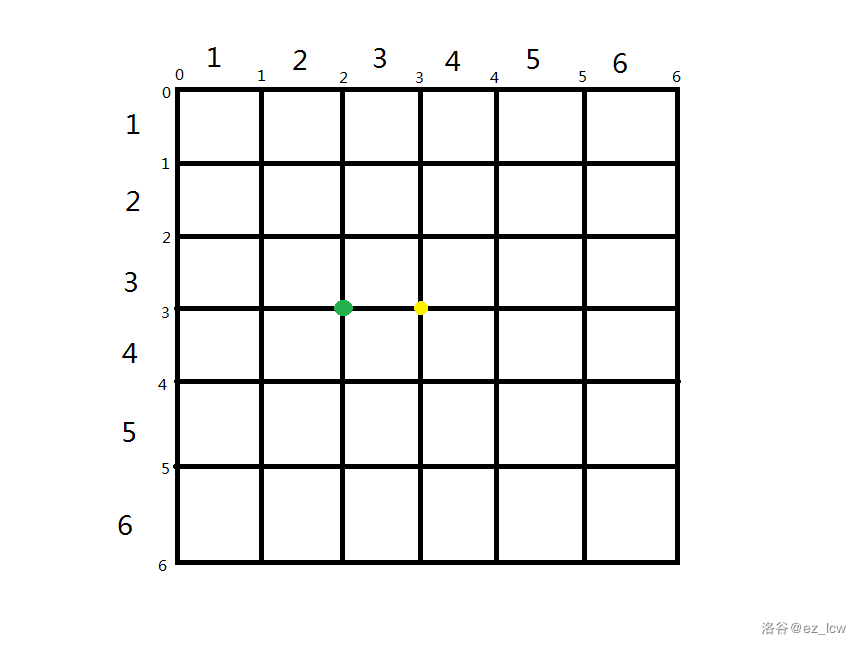
如图,我们现在要求出 (黄点),那么只能从 (绿点)转移,因为分割线最后的方向是向右的。
第一种情况:从 转移,如图:
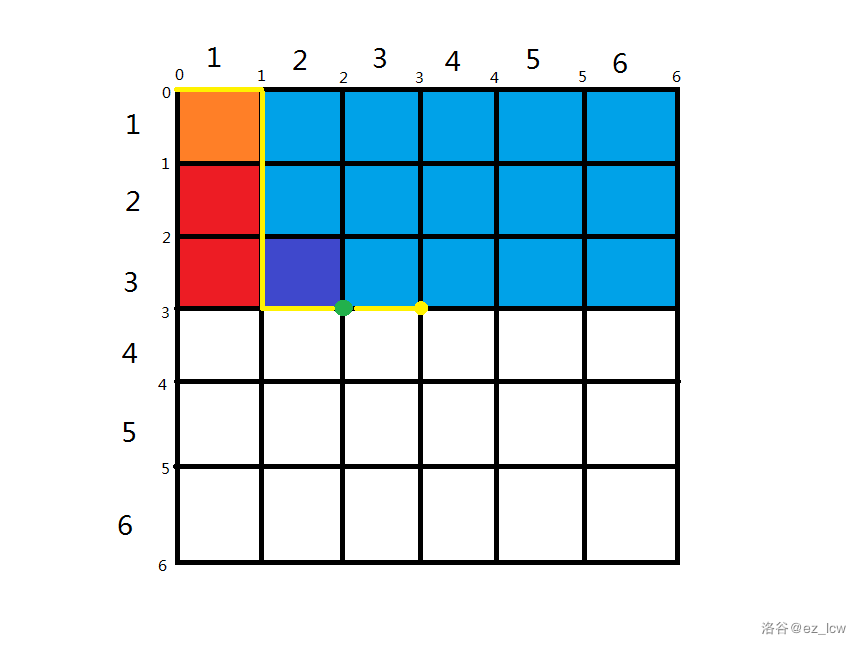
那么显然有 ,因为 没变, 也没变。
第二种情况:从 转移,如图:
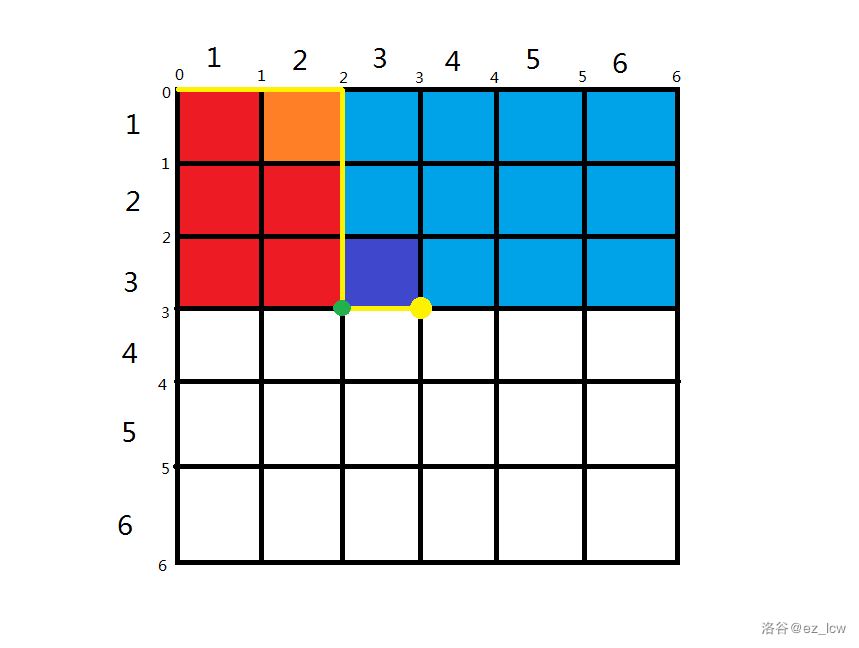
我们发现,原来的分割线终止在 时,,就是只有 一个灌溉器,但是现在分割线种植在 时,,也就是新增了一个灌溉器 。那么原来的方案数 ,现在 ,所以 。
整合一下,就有 。
即
-
考虑 怎么转移:
同理,这次需要从绿点转移:
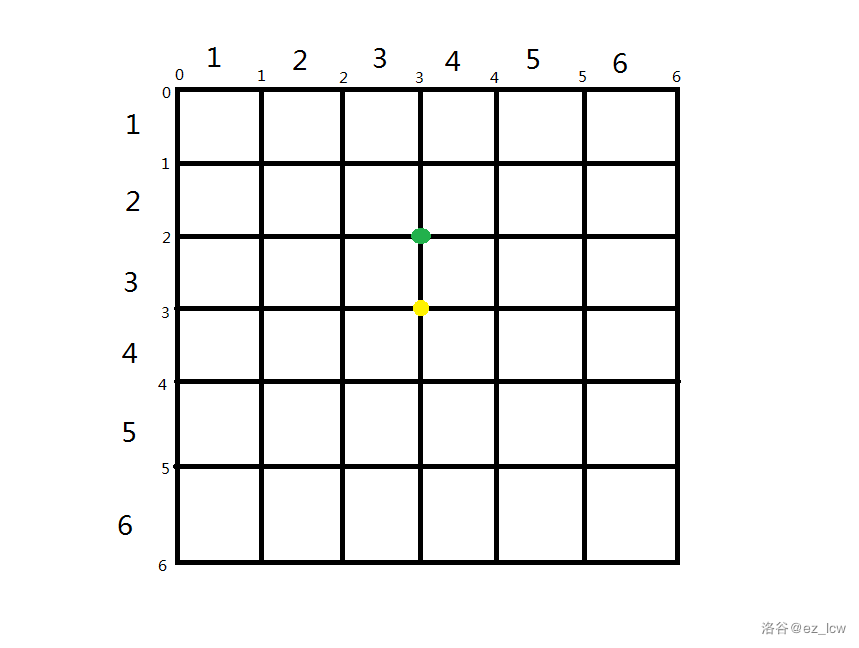
第一种情况:从 转移,如图:
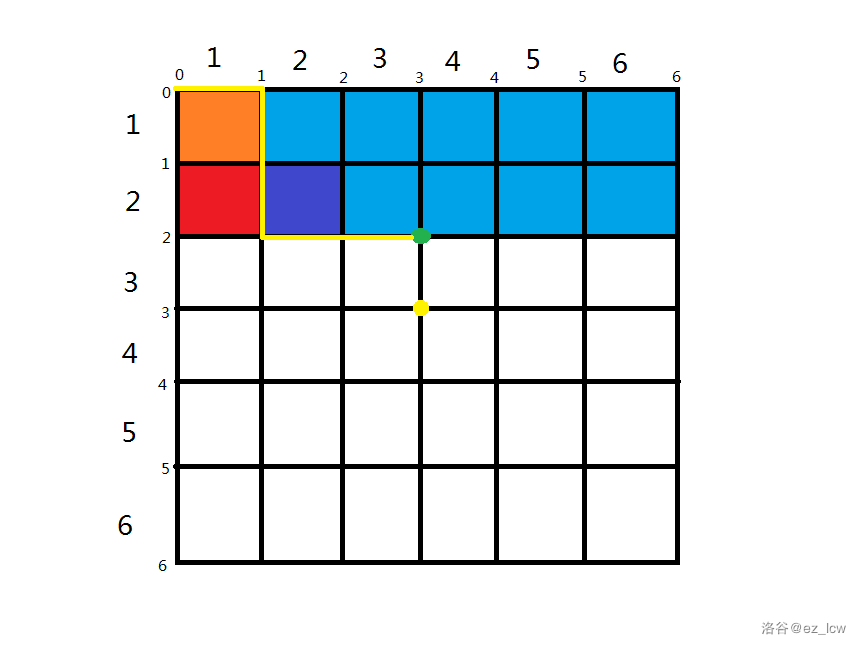
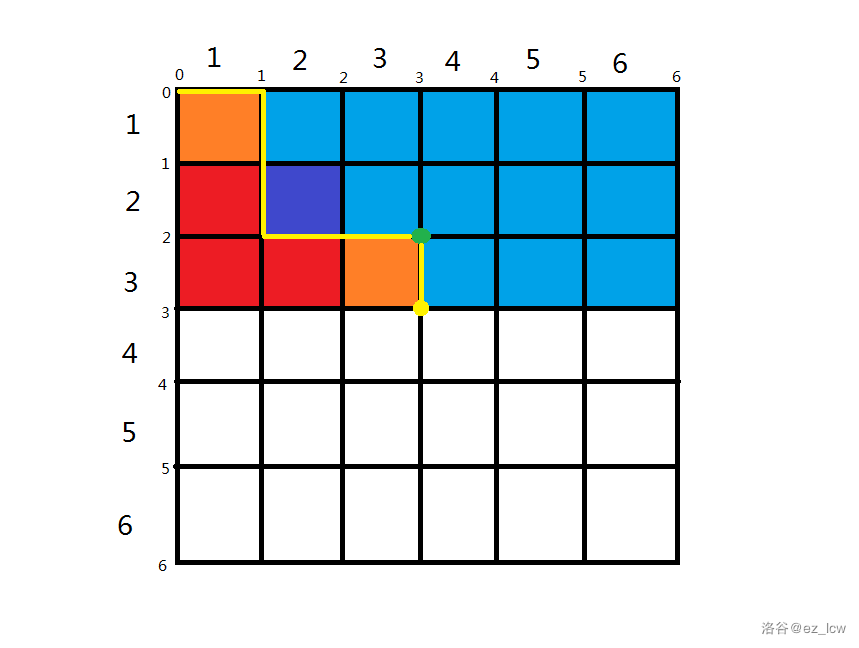
第一幅图是 的情况,第二幅图是 的情况。
显然从第一幅图变成第二幅图时 增加了 , 增加了 ,那么 值从 变成了 ,也就是说 。
第二种情况:从 转移,如图:
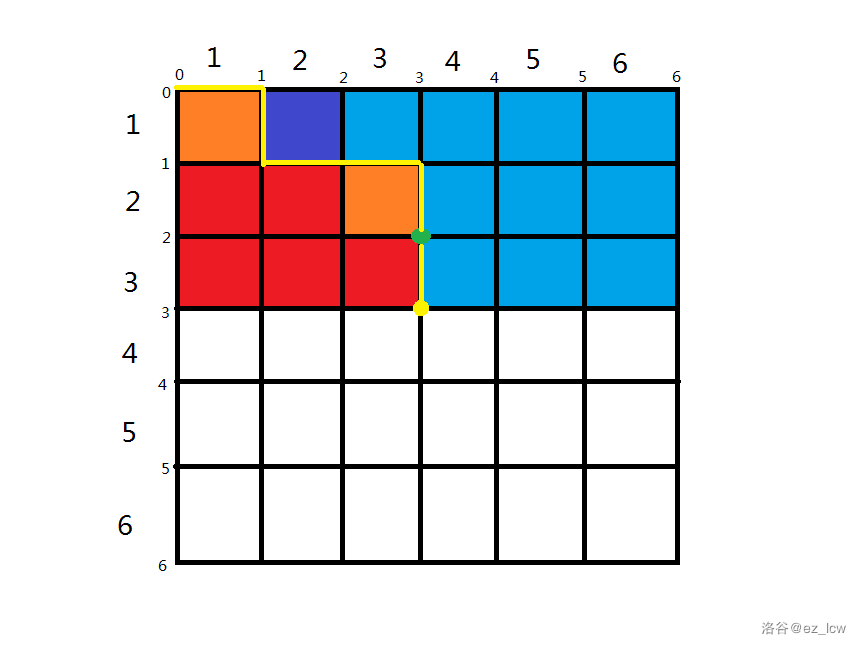
然后我们发现,, 没变,则
整合一下,$dp(3,3,1)=dp(2,3,0)\times 2^{sum_3-1}+dp(2,3,1)\times 2^{sum_3}$。
即 $dp(i,j,1)=dp(i-1,j,0)\times 2^{sum_i-1}+dp(i-1,j,1)\times 2^{sum_i}$。
到这里,整道题就做完了,已经可以 AC 了。
时间复杂度 。
但是还有一些可以优化的地方,这里就大致讲一下,就是把求面积的部分直接提出来,放到最后输出的时候乘上一个 (也就是全局的面积)就好了。
代码(未加优化):
#include<bits/stdc++.h> #define N 2010 #define mod 1000000007 #define half 500000004 using namespace std; void add(int &a,int b){a=(0ll+a+b)%mod;} int mul(int a,int b){return (1ll*a*b)%mod;} int n,dp[N][N][2],sum[N],poww[N*N]; char ch[N][N]; int main() { scanf("%d",&n); poww[0]=1; for(int i=1;i<=n*n;i++) poww[i]=mul(2,poww[i-1]); for(int i=1;i<=n;i++) { scanf("%s",ch[i]+1); for(int j=1;j<=n;j++) sum[i]+=(ch[i][j]=='.'); } dp[0][0][0]=dp[0][0][1]=1; for(int i=0;i<=n;i++) { for(int j=0;j<=n;j++) { if(!i&&!j) continue; if(j>0) { add(dp[i][j][0],dp[i][j-1][0]); if(ch[i][j]=='.') add(dp[i][j][0],mul(dp[i][j-1][1],half)); } if(i>0) { add(dp[i][j][1],mul(dp[i-1][j][1],poww[sum[i]])); if(ch[i][j]=='.') add(dp[i][j][1],mul(dp[i-1][j][0],poww[sum[i]-1])); } } } printf("%d\n",(0ll+dp[n][n][0]+dp[n][n][1])%mod); return 0; }代码(加优化):
#include<bits/stdc++.h> #define N 2010 #define mod 1000000007 #define half 500000004 using namespace std; void add(int &a,int b){a=(0ll+a+b)%mod;} int mul(int a,int b){return (1ll*a*b)%mod;} int n,dp[N][N][2],sum; char ch[N][N]; int poww(int a,int b) { int ans=1; while(b) { if(b&1) ans=(1ll*ans*a)%mod; a=(1ll*a*a)%mod; b>>=1; } return ans; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%s",ch[i]+1); for(int j=1;j<=n;j++) sum+=(ch[i][j]=='.'); } dp[0][0][0]=dp[0][0][1]=1; for(int i=0;i<=n;i++) { for(int j=0;j<=n;j++) { if(!i&&!j) continue; if(j>0) { add(dp[i][j][0],dp[i][j-1][0]); if(ch[i][j]=='.') add(dp[i][j][0],mul(dp[i][j-1][1],half)); } if(i>0) { add(dp[i][j][1],dp[i-1][j][1]); if(ch[i][j]=='.') add(dp[i][j][1],mul(dp[i-1][j][0],half)); } } } printf("%d\n",1ll*(dp[n][n][0]+dp[n][n][1])%mod*poww(2,sum)%mod); return 0; }其实就是常数上的优化。写码不易,留赞再走。 -
- 1
信息
- ID
- 5325
- 时间
- 2000ms
- 内存
- 250MiB
- 难度
- 5
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
