自动搬运

查看原文

来自洛谷，原作者为

	KobeBeanBryantCox 请牢记：你曾在 OI 的星空中留下过属于自己的轨迹。

搬运于2025-08-24 22:18:58，当前版本为作者最后更新于2024-07-27 14:28:29，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P6246 [IOI2000] 邮局 加强版 加强版 题解

---

update on 2025-08-09：修正了错误的代码。之前错误的原因包括但不限于二分队列的边界问题。

感谢这个、这个、这个对本题解的贡献。本来还想改一下图的（感觉字太丑了）但是有点懒。

题目传送门。

我这个题做了 5 个小时 15 分钟，其中 4 小时 30 分钟理解做法，45 分钟敲代码。

我是不是好菜啊啊啊。。。

---

题意

题意不方便表述，还是直接去看原题的题目描述吧。。。

---

解法

wqs 二分 + 二分队列。

一

考虑暴力的 DP 转移，$f_{i,j}$ 表示前 $i$ 个村庄建立 $j$ 个邮局的最小距离和。

$$f_{i,j}=\min_{1\leq k\leq i}\{{f_{k-1,j-1}+w_{k,i}\}} $$

答案则是 $f_{n,m}$。

其中 $w$ 满足四边形不等式，所以 $f$ 具有凸性。

记 $K_{i,j}=\arg\min_{1\leq k\leq i}\{{f_{k-1,j-1}+w_{k,i}\}}$（$\arg$ 表示最优决策点。）

感性理解发现题目具有决策单调性，即 $K_{i-1,j}\leq K_{i,j}\leq K_{i,j+1}$。

只利用 $K_{i-1,j}\leq K_{i,j}$ 可以分治优化决策单调性，复杂度 $O(nm\log n)$。

同时利用两个条件，调整 DP 顺序（即四边形不等式优化），可以做到 $O(n(n+m))$ 的 DP。

但是优化还不够。

设 $g_i$ 表示 $n$ 个村庄放 $i$ 个邮局的最小距离和。注意到 $g$ 是凸函数。直接计算 $g_m$ 复杂度过高。

考虑构造一个新函数 $g'$，先算出 $g'_m$，再算 $g_m$。

考虑构造如下的新问题：

$n$ 个村庄放若干个邮局（不限制个数），但每个放邮局会增加 $t$ 的代价。最小化总代价加距离和。

这个问题是可以 $O(n)$ DP 求解的，并且它计算的是 $\min_i\{g_i+ti\}$。

那只要让 $\min_i\{g_i+ti\}=g_m+tm$，就可以求出 $g_m$。

注意到 $g_i+ti$ 也是凸的（证明后面会讲），所以 $t$ 越大，最小值横坐标越小。

故满足单调性，考虑二分 $t$。

以上是 wqs 二分的证明及过程，下面讲讲构造的新问题的解法。

二

$n$ 个村庄放若干个邮局（不限制个数），但每个放邮局会增加 $t$ 的代价。最小化总代价加距离和。

考虑前 $i$ 个村庄：$f_i=\min_{1\leq k\leq i}\{f_{k-1}+w_{w,i}+t\}$。

其中 $w$ 可以 $O(1)$ 计算（计算方法后面会将）。

记 $K_i=\arg\min_{i\leq k\leq i}\{f_{k-1}+w_{w,i}+t\}$，那么有 $K_{i-1}\leq K_i$。

考虑维护一个集合 $I_k=\{i\in[1,n]:K_i=k\}$ 表示最优决策点为 $k$ 的 $i$。因为题目具有决策单调性，所以这个集合一定是一个区间。

不妨把这个区间记做 $[L_k,R_k]$。

对于已经算出来的 $f_k$，如果已知 $[L_k,R_k]$，那么可以对于 $i\in[L_k,R_k]$ 在 $O(1)$ 时间内算出 $f_i$。而已知 $R_k$，可以二分算出 $R_{k+1}$。只需要找到 $i>R_k$，且 $k+2$ 比 $k+1$ 更优的那个点即可。

上面那句话（指的是从 “ 不妨 ” 开始到这里）没看懂怎么办？没关系，往下看。（看懂的大佬可以直接跳到代码。）

具体化地，根据决策单调性的性质，有 $\forall i<j,R_i\leq L_j$，换句话说，存在一个点 $pos$ 为 $i<j$ 的最优决策点的划分点。

考虑使用一个队列维护 $(i,L_i,R_i)$ 三元组，记为 $qk,ql,qr$。

转移到 $i$ 时，弹出队头直到 $i\in[ql_{head},qr_{head}]$，此时队头是 $i$ 的最优决策，直接转移。

考虑更新队列，如果整个最优决策区间都比 $i$ 要劣，即从 $i$ 转移到 $ql_{tail}$ 优于从 $qk_{tail}$ 转移到 $ql_{tail}$，一直弹出队尾直到不符合条件。

画个图（右边是 $tail$）：

现在删去了队尾完全无用的转移点，考虑有一个转移区间有些有用有些没用，即 $\exists pos\in[ql_{tail}+1,qr_{tail}]$，满足对于 $pos$ 之前的转移用原来的 $qk_{tail}$ 更优，之后的转移用 $i$ 更优。

显然这样的 $pos$ 满足单调性，故可以二分找到。找到后把区间剖开，加入新元素即可。

画个图：

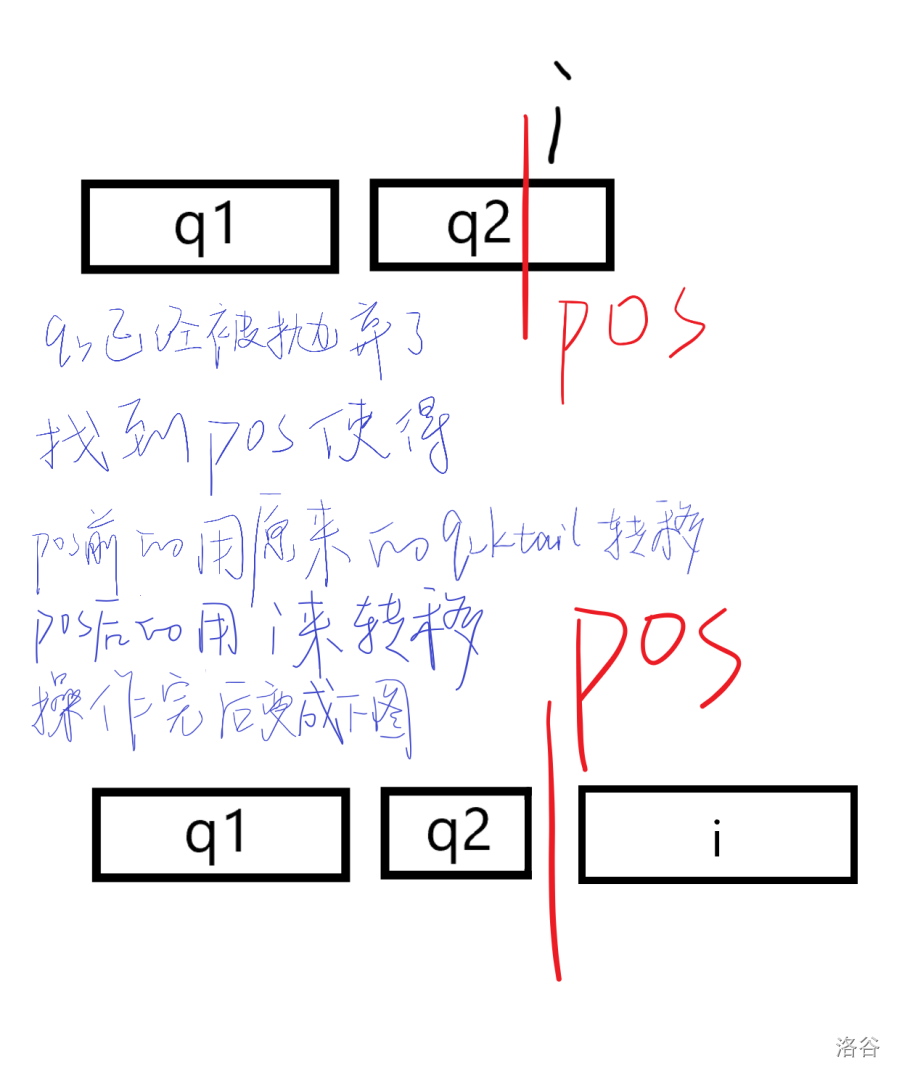
别说我字丑，电脑写字不方便，不知道为什么不能输入字只能写。

复杂度：wqs 二分 + 二分队列，一共是 $O(n\log V\log n)$。

---

补充

一、关于 $g_i+ti$ 也是凸的的证明

由于 $g_i$ 是凸的~~（这个显而易见吧，不懂的看其他题解）~~，那么有 $g_i-g_{i-1}\leq g_{i+1}-g_i$

$\Rightarrow g_i-g_{i-1}+t\leq g_{i+1}-g_i+t$

$\Rightarrow (g_i+ti)-(g_{i-1}+(i-1)t)\leq (g_{i+1}+(i+1)t)-(g_i+ti)$

故 $g_i+ti$ 也是凸的。

二、关于 $w$ 的 $O(1)$ 计算

显然在这段区间的中位数处放邮局使得总距离最短。

令 $x=\lfloor\frac{l+r}{2}\rfloor$。

则左半部分对 $w$ 的贡献为 $a[x]-a[l]+a[x]-a[l+1]+\dots+a[x]-a[x-1]=a[x]\times(x-l)-\sum_{i=l}^{x-1}a[i]$。

其中，$a$ 是原数组。

求和部分用前缀和预处理一下，右半部分同理可得。

所以 $w_{i,j}=a[x]\times(x-l)-(s[x-1]-s[l-1])+a[x]*(r-x)-(s[r]-s[x])$。

其中，$s$ 是前缀和数组。

三、wqs 二分整数而不是实数的证明

其实可以二分实数，不过有可能 TLE。

我们知道，答案 $f_i$ 是整数，那么 $f_i-f_{i-1}$ 也是整数。

即 $\LARGE\frac{f_i-f_{i-1}}{i-(i-1)}$是整数，即斜率是整数。

我们 wqs 二分的就是斜率，因此本题可以二分整数。对于答案是实数的，可能要使用实数域的二分，同时要控制二分次数，不要 TLE。

---

AC 代码

// update on 2025-08-09 修改了代码
#include<bits/stdc++.h>
#define Code using
#define by namespace
#define wjb std
Code by wjb;
#define int long long // 十年 oi 一场空，不开 long long 一场空！
int in()
{
	int k=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9')
	{
		if(c=='-')f=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9')k=k*10+c-'0',c=getchar();
	return k*f;
}
void out(int x)
{
	if(x<0)putchar('-'),x=-x;
	if(x<10)putchar(x+'0');
	else out(x/10),putchar(x%10+'0');
}
const int N=5e5+10;
int n,m;
int a[N];
int sum[N]; // 前缀和数组
struct node{int k,l,r;}; // 用于队列
deque<node>q; // 要开双向队列
int w(int l,int r) // O(1) 计算 w
{
	int md=(l+r)>>1;
	int d1=(md-l)*a[md],d2=(r-md)*a[md];
	int s1=sum[md-1]-sum[l-1],s2=sum[r]-sum[md];
	return d1-s1+s2-d2;
}
int f[N],h[N]; // f 是最优距离加代价，h 是放的邮局的个数
bool check(int i,int j,int k){return f[i]+w(i+1,k)<=f[j]+w(j+1,k);} // 比较是否更优的函数
int ff(int t)
{
	while(!q.empty())q.pop_front();
	q.push_back((node){0,1,n}),f[0]=0;
	for(int i=1;i<=n;i++)
	{
		while(!q.empty()&&q.front().r<i)q.pop_front(); // 找到 i 的最优决策
		int j=q.front().k;
		f[i]=f[j]+w(j+1,i)+t,h[i]=h[j]+1;
		while(!q.empty()&&check(i,q.back().k,q.back().l))q.pop_back(); // 删掉完全无用的区间
		if(q.empty()){q.push_back((node){i,1,n});continue;}
		int l=q.back().l,r=n,ans=n+1;
		while(l<=r) // 二分查找 pos
		{
			int mid=(l+r)>>1;
			if(check(q.back().k,i,mid))ans=mid,l=mid+1;
			else r=mid-1;
		}
		if(ans<n)q.back().r=ans,q.push_back((node){i,ans+1,n}); // 剖开区间插入 i
	}
	return h[n];
}
int two(int l,int r) // wqs 二分
{
	int res=0;
	while(l<=r)
	{
		int mid=(l+r)>>1;
		if(ff(mid)<=m)res=mid,r=mid-1;
		else l=mid+1;
	}
	ff(res);
	return f[n]-res*m;
}
signed main()
{
	n=in(),m=in();
	for(int i=1;i<=n;i++)a[i]=in(),sum[i]=sum[i-1]+a[i];
	out(two(0,1e12)); // 这个值域我也搞不清楚到底要开多大
	return 0;
}

---

后记

1. 十年 oi 一场空，不开 long long 一场空！

2. 如果有讲述不清楚的，欢迎提问；如果有讲述错误的，欢迎提出修正。

3. 能不能顺手点个赞评论一下，关注一下 QWQ