自动搬运

查看原文

来自洛谷，原作者为

	yangjintian ·-· 菜

搬运于2025-08-24 22:18:46，当前版本为作者最后更新于2023-07-25 13:46:49，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

原题链接

题目大意：

一颗 $N$ 个节点的以 $E$ 为根的树，每条边有权值 $W_i$，有 $S$ 个特殊点和 $Q$ 次询问。 每次询问第 $I$ 条边不能经过，并给定一个起点 $R$。

1.若能走到根节点，则输出 escaped。

2.若走不到根节点也走不到任意个特殊点，则输出 oo。

3.若走不到根节点但能走到特殊点，则输出最近特殊点的距离。

解题思路：

先给张图，方便理解（图很丑，看懂就行 QWQ）

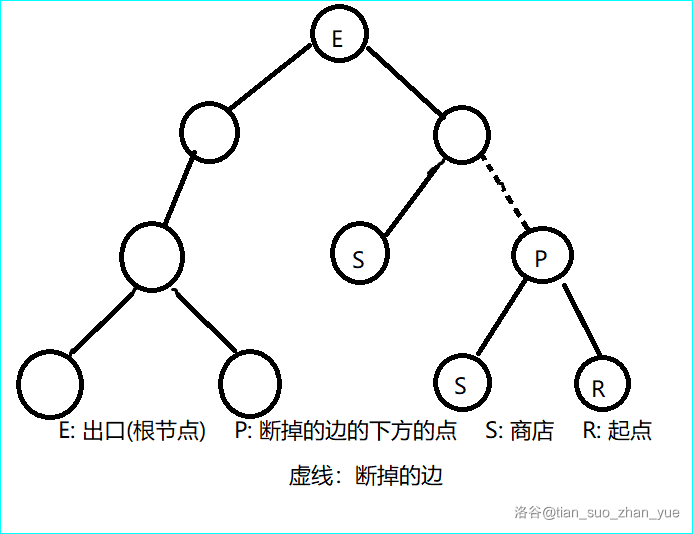
我们设深度大的那个点为 $P$。

第一种情况输出 escaped ：

那就说明 $R$ 到 $E$ 的路没被断开，也就是 $R$ 不在 $P$ 的子树内，所以 $\operatorname{lca}(R , P) \ne P$。 $\,$

第二种情况输出 oo ：

到不了根节点且到不了特殊点，说明 $R$ 在 $P$ 的子树内，即 $\operatorname{lca}(R , P) = P$ 且 $P$ 的子树内（包含 $P$）没有商店。 $\,$

第三种情况：

到不了根节点，但能到特殊点。

找的特殊点的范围一定在 $P$ 的子树内,即 $\operatorname{lca}(R , P) = P$。

暴力 DFS 找复杂度是 $O(n^2)$ 的，考虑优化，这种树上问题的优化很多很多都是用倍增的。

注意到 $ans = \min(c[R] - c[i] + nearshop[i])$。

其中 $i$ 为 $R$ 的祖先（包括 $R$）,$c[i]$ 表示从 $i$ 到根节点的距离，$nearshop[i]$ 表示子树内离 $i$ 最近的特殊点的距离。

$c[R]$ 可以提出来，那只要倍增找最小的 $nearshop[i] - c[i]$ 就可以了。

我们可以设 $go[i][j]$ 表示从节点 $i$ 往上走 $2^j$ 步到的点，$f[i][j]$表示 $i$ ~ $go[i][j]$ 的所有节点中最小的 $nearshop[i] - c[i]$。

最终答案即为 $c[R]$ + 找到的最小 $nearshop[i] - c[i]$。

易错 or 代码中难理解的点（☆）

• 开 long long。
• 找最近特殊点必须只找子树内的，找外面的如果边被断开就没办法了，倍增的话就倍增到 $P$ 就行了。或者其实那个子树外的特殊点是合法的，但那下次往上跳的时候一定会统计到的。
• 当 $P = R$ 时，答案是不会更新的，所以手动判断一下。

代码实现（细节有点多，放注释里了，非常仔细的，看一看吧 QWQ）:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int Num = 1e5 + 5;
int n, s, q, e;
int go[Num][20], dep[Num], u[Num], v[Num], shop_num[Num];
// shop_num[i] 表示i及i的子树内有多少商店 
ll c[Num], near_shop[Num], f[Num][20], p[Num]; //这几个都要开long long!!! 
//!!!只用统计子树内的最近商店，子树外的以后会统计到或根本用不到
bool mark[Num];
struct edge {
	int to;
	ll w;
};
vector<edge> g[Num];
inline ll read() {
	ll s = 0, f = 1; char c = getchar();
	while (c < '0' || c>'9') { if (c == '-')f = -1; c = getchar(); }
	while (c >= '0' && c <= '9') { s = s * 10 + c - '0'; c = getchar(); }
	return s * f;
}
void dfs_pretreat(int x, int fa) {   //pretreat  v.预处理
	go[x][0] = fa; dep[x] = dep[fa] + 1;
	if (mark[x])shop_num[x]++;
	for (int i = 0; i < g[x].size(); i++) {
		int t = g[x][i].to;
		if (t == fa)continue;
		c[t] = c[x] + g[x][i].w;
		dfs_pretreat(t, x);
		shop_num[x] += shop_num[t];
	}
}
void dfs_shop(int x, int fa) {
	if (mark[x])near_shop[x] = 0;
	for (int i = 0; i < g[x].size(); i++) {
		int t = g[x][i].to;
		if (t == fa)continue;
		dfs_shop(t, x);
		near_shop[x] = min(near_shop[x], near_shop[t] + g[x][i].w);
		//只找子树内的最近商店
	}
}
int lca(int x, int y) {
	if (dep[x] < dep[y])swap(x, y); //让x成为深度大的点
	for (int i = 18; i >= 0; i--)if (dep[go[x][i]] >= dep[y])x = go[x][i];
	for (int i = 18; i >= 0; i--)if (go[x][i] != go[y][i])x = go[x][i], y = go[y][i];
	return (x == y) ? x : go[x][0];
}
void solve(int I, int R) {
	if (dep[u[I]] < dep[v[I]])swap(u[I], v[I]);
	int point = u[I];
	int LCA = lca(R, point);
	if (LCA != point) {  //escaped 优先级大于 oo
		cout << "escaped\n";
		return;
	}
	if (LCA == point && shop_num[point] == 0) {
		cout << "oo\n";
		return;
	}
	ll ans = (ll)0x3f3f3f3f3f3f, pos = R;
	for (int i = 18; i >= 0; i--) {
		if (dep[go[pos][i]] >= dep[point]) {
			ans = min(ans, f[pos][i]);  //先更新再跳
			pos = go[pos][i];
		}
	}
	if (point == R)ans = near_shop[R] - c[R]; //往上跳不了时
	cout << ans + c[R] << endl;
}
int main() {
	n = read(), s = read(), q = read(), e = read(); //e是根节点
	for (int i = 1; i < n; i++) {
		u[i] = read(), v[i] = read();
		int w = read();
		g[u[i]].push_back(edge{ v[i],w });
		g[v[i]].push_back(edge{ u[i],w });
	}
	for (int i = 1; i <= s; i++)mark[read()] = 1;
	dfs_pretreat(e, e);   //e是根节点
	memset(near_shop, 0x3f, sizeof(near_shop)); //要设为无穷大!!!
	dfs_shop(e, e);		  //!!!只用统计子树内的最近商店，子树外的以后会统计到
	for (int t = 1; t <= 18; t++)
		for (int i = 1; i <= n; i++)
			go[i][t] = go[go[i][t - 1]][t - 1];
	for (int i = 1; i <= n; i++)p[i] = near_shop[i] - c[i];  
	//p临时存一下，因为f[i][t]需要表示走2^t步 
	for (int i = 1; i <= n; i++)f[i][0] = min(p[i],p[go[i][0]]);
	//如果i为商店,f[i][0]不需要置为0!!!
	for (int t = 1; t <= 18; t++)
		for (int i = 1; i <= n; i++)
			f[i][t] = min(f[i][t - 1], f[go[i][t - 1]][t - 1]);
	//找c[R] + min{ near_shop[i] - c[i]  }  i∈子树 v[I]
	//f[i][j] 表示在 i ~ go[i][j] 这些点中， (near_shop[]-c[]) 最小是多少(典型倍增思想)，最后加上c[R]就为最终answer
	while (q--) {
		int a = read(), b = read();
		solve(a, b);
	}
	return 0;
}

推荐一些树上问题的有意思的题目QWQ