自动搬运

查看原文

来自洛谷，原作者为

	Feyn AFO

搬运于2025-08-24 22:18:40，当前版本为作者最后更新于2022-09-29 18:26:26，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

双倍经验，一模一样

说一下模拟赛场上和场下关于这道题的心路历程。

$15$ 分应该是很容易的。考虑把 $1$ 和 $N$ 放在两边，然后在中间放一些点，然后这些点分别和起终点连边，显然这样每条支路就会有一个长度为 $3$ 的合法序列，于是最后的答案就是支路数减一，点数和边数都和输入是同级的。

然后我就开始思考能不能把这玩意拆分成几个部分，一顿手玩之后发现一种妙的图，具体构造方法是三个点为一列，列和列之间完全连边，不相邻的列不连边。大概长这样：

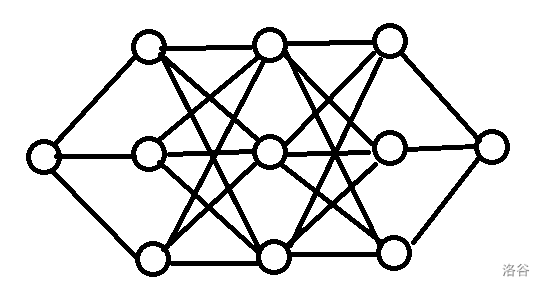
发现这种图有一个性质，随着列数越来越多，整体的答案会是 $1\ -2\ \ 4\ -8\dots$ 这样的，十分有规律。而我们知道这个图形有一个性质，即各部分的贡献可以累加。于是就可以把询问的数拆分成许多数之和，然后就对各部分进行处理即可。于是考场上得了 $48$ 分，代码就不放了。

场下看了别人的代码并结合了官方的题解，却仍然久久未能明白，特别是那句 we can add two nodes to a new level that are connected to all from the previous level 中的 previous 具体指什么百思不得其解（我太弱了），在咨询其它大佬之后用我的语言给出这道题的完整解法：

其实考场上的代码已经很靠近正解了，只是没有把问题进行很好的具象分析。我们可以令 $f_{x,0/1}$ 代表序列最后一个节点是 $x$，并且序列长度奇偶性确定时的方案数，转移就是枚举所有能到达 $x$ 的 $y$，$f_{x,p}=\sum f_{y,1-p}$。然后发现没必要加上后面那一维，所以我们可以令 $g_x$ 是 $f_{x,1}$ 和 $f_{x,0}$ 的差，那么方程就变成了 $g_x=-\sum g_y$。

观察上面那个模型，发现任意一个点都可以被前面任意一层的任意节点到达，所以可以记 $sum_x$ 为前 $x$ 层 $g$ 值总和，那么第 $x+1$ 层的 $g$ 值应该是 $-sum_x$，更新一下就有 $sum_{x+1}=sum_x-sum_x\times q=(1-q)sum_x$（假设每层的节点个数是 $q$）。有两个特殊值：$q=3$ 时会让总和扩大一倍，而 $q=2$ 时会让总和取反，我们可以利用这两个操作来构造出输入值。

显然越靠前的位置对答案的影响越大，考虑特殊情况，即 $K=2^r$ 的情况，显然我们可以一开始用一个 $q=3$ 的层，然后一直用 $r$ 次，这样可以保证得到的结果绝对值一定是 $K$，如果正负不对的话直接用 $q=2$ 的做法取反即可。

然后思考如何推广上述流程，也就是如何在一个二进制位上放一。通过第一个 subtask 的经验，任意一个直接和起点相连的边都对答案有一个负的贡献，那么假如当前的总和是负的，那么我们在本层添加一个直接和 $1$ 相连的点就可以了；如果总和是负的，那么直接通过操作把总和取反之后就是前面的问题了。

其它的就没什么了，有些细节需要自己思考一下，但如果理解了那些问题就很简单了。

代码比较短，由于某些原因压了点行，不影响可读性。

#include<bits/stdc++.h>
//#define feyn
#define int long long
#define adding for(int x:last)for(int y:now)ans.push_back((node){x,y})
using namespace std;
inline void read(int &wh){
	wh=0;char w=getchar();int f=1;
	while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
	while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar();}
	wh*=f;return;
}

int m,cnt=1;

struct node{int a,b;};
vector<int>endll,last,now;
vector<node>ans;

signed main(){
	
	#ifdef feyn
	freopen("in.txt","r",stdin);
	#endif
	
	read(m);
	if(m==0){printf("3 2\n1 2\n 2 3\n");return 0;}
	if(m==1){printf("1 0\n");return 0;}
	if(m==-1){printf("2 1\n1 2\n");return 0;}
	bool neg=false,op=false;if(m<0)m=-m,neg=true;
	int lg=1;while((1ll<<lg)<=m)lg++;lg--;
	
	for(int i=lg-1;i>=0;i--){
		now.clear();for(int j=0;j<3;j++)now.push_back(++cnt);
		if(i==lg-1)for(int x:now)ans.push_back((node){1,x});else adding;
		if(((1ll<<i)&m)==0){last=now;op^=1;continue;}
		if(op){last=now;now.clear();for(int j=0;j<2;j++)now.push_back(++cnt);adding;}
		now.push_back(++cnt);ans.push_back((node){1,cnt});last=now;op=true;
	}
	if(neg==op){now.clear();for(int i=0;i<2;i++)now.push_back(++cnt);adding;}
	++cnt;for(int x:now)ans.push_back((node){x,cnt});
	printf("%lld %lld\n",cnt,ans.size());
	for(node x:ans)printf("%lld %lld\n",x.a,x.b);
	
	return 0;
}