自动搬运

查看原文

来自洛谷，原作者为

	Feather_Moon I dreamed.

搬运于2025-08-24 22:18:25，当前版本为作者最后更新于2025-07-04 19:26:27，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

本蒟蒻的第一篇题解，求求管理员大大审核通过 QAQ。

P6193 [USACO07FEB] Cow Sorting G 解题报告。

题意

有一个长度为 $n$（$1 \leq n \leq 10^5$）的序列，第 $i$ 个数有一个权值 $a_i$（$1 \leq a_i \leq 10^5$, $a_i$ 互不相同）。你可以花费 $a_i+a_j$ 的代价去交换第 $i$ 个元素和第 $j$ 个元素，求将 $a$ 升序排序的最小代价。

分析

这个 $a_i+a_j$ 的代价就很烦，我们先考率题目的弱化。

弱化版

如果不管代价，只要求交换次数最少，答案是什么呢？

举一个例子：

数列 $\{5,1,4,3,2\}$，最少需要三次操作。

第一次操作：交换 $3$ 和 $4$，数列变成 $\{5,1,3,4,2\}$。

第二次操作：交换 $1$ 和 $5$，数列变成 $\{1,5,3,4,2\}$。

第三次操作：交换 $2$ 和 $5$，数列变成 $\{1,2,3,4,5\}$。

可以证明不存在更少的操作次数。

可以发现，我们的操作策略就是把一个元素移到它该去的地方。

我们将一个元素与它要去的位置所在的元素连边（如元素 $5$ 要与在第 $5$ 个位置的元素 $2$ 连边），如下图：

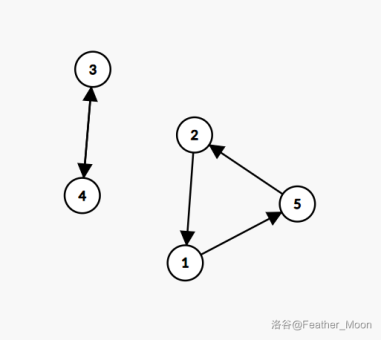
我们可以发现，图是由若干个环组成的。

感性证明也非常简单，每个点被连一次，出去一次，入度和出度均是一，这样的图只能是若干个环组成的。

观察上图的环，以环 $2 \rightarrow 1 \rightarrow 5 \rightarrow 2$ 举例子。

我们可以发现 $2,5,1$ 虽然不在自己应该在的位置，但是如果把它们看成整体，对于整个序列来说它们占据了排好序后 $2,5,1$ 应该在的位置，所以对于整个序列来说是有序的，它们只是自身内部无序而已。所以只需要环内换序就可以了。

而对于一个含有 $n$ 个元素的环，只要交换 $n-1$ 次（一次操作排好一个元素，最后一个不用排）。所以，答案就是元素的数量减去环的数量。

严格的证明较复杂，可以参考 这篇文章。

弱化版核心代码：

ans=n;
for(int i=1;i<=n;i++){
	if(vis[i])continue;
	int now=i;ans--;
	while(!vis[now]){
		vis[now]=1;//打标记
		now=a[now];//遍历下一个结点
	}
}

由于每个结点只经过一次，时间复杂度是 $\mathcal{O}(n)$ 的。

原题

扯了这么多，让我们回到正轨。

我们将上面的方法迁移过来，先找到一个元素它排序后在哪里，这可以用二分或排序解决，然后建环。

那么现在的问题就变成了：

把一个环内的元素有序排列的最小代价。

每个元素要回到原位置，最少也得交换一次。而像这样简单强势的交换，一共有 $siz-1$ 次（$siz$ 是环的大小）。只需要利用圈里面最小的那个当苦力参与交换即可，此时代价为 $(siz - 2)\times Min + Sum$，其中 $Sum$ 表示环中所有元素之和，$Min$ 表示环中最小的元素（$Min$ 与其它所有元素做了 $siz-1$ 次交换，$Sum$ 中包含了一个 $Min$，所以是 $(siz - 2)\times Min + Sum$）。

当你自信满满的拿着代码甩在这道题脸上时，你会发现这道题拿着 WA 甩了你一脸。

问题出在哪呢？我们来看下面这个图：

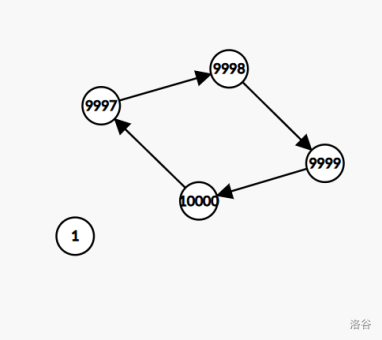
按照我们原来的的方式，我们会拿 $9997$ 分别与 $9998$ 到 $10000$ 进行交换，代价是 $(9997+ 9998)+(9997 + 9999)+(9997 + 10000)=59988$。如果我们将外面的 1 介入呢：

1.先将外部最小的与内部最小的交换，代价为 $(1+9997)=9998$。

2.再将外部最小代替以前内部最小进行交换，代价为 $(1+9998)+(1+9999)+(1+10000)=30000$。

3.最后将外部最小的与内部最小交换回来，代价为 $(1+9997)=9998$。

总代价为 $9998+30000+9998=49996 < 59988$。

关于为什么要与内部最小的交换的简要证明：

设外部最小 $Min$（这应该很好理解）与内部权值为 $X$ 的元素交换。

• 第一、三步的代价为 $Min+x$。

• 第二步的代价为 $(siz-2)\times Min+(Sum-x+Min)$（定义同上）。

总代价为 $x+(siz+1)\times Min+Sum$。

由于 $Sum,siz,Min$ 是定值，当 $x$ 最小时代价最小。

所以，共有两种调换办法，大部分人都会想到利用圈里面最小的那个参与交换，还有一个办法就是把全局最小的调入圈里，弄好了再还回去。

此时，代价为 $\min(Sum+( siz - 2 ) \times Min1,(siz+1)\times Min2+Sum+Min1)$，其中 $siz$ 是环的大小， $Sum$ 表示环中所有元素之和，$Min1$ 表示环中最小的元素，$Min2$ 表示全局最小的元素。

每个元素只折腾一次，故核心时间复杂度为 $\mathcal{O}(n)$。

瓶颈在于排序或二分的 $\mathcal{O}(n \log n)$。

注意开 long long。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=200005;
int n,b[maxn],a[maxn],nxt[maxn],ans,Min1=(int)1<<60;;
bool vis[maxn];
int read(){
	char ch=getchar();int ret=0,f=1;
	while(ch<'0'||ch>'9'){if(ch=='-') f=-f;ch=getchar();}
	while(ch>='0'&&ch<='9') ret=ret*10+(ch&15),ch=getchar();
	return ret*f;
}
int find(int x){//二分枚举每个数排序后的排名
	int L=1,R=n,mid,ans;
	while(L<=R){
		mid=L+R>>1;
		if(b[mid]==x)return mid;
		if(b[mid]<x)L=mid+1; 
		if(x<b[mid])R=mid-1;
	}
}
signed main(){
//	freopen("csort.in","r",stdin);
//	freopen("csort.out","w",stdout);
	n=read();
	for(int i=1;i<=n;i++)b[i]=a[i]=read(),Min1=min(Min1,a[i]);
	sort(b+1,b+1+n);
	for(int i=1;i<=n;i++)nxt[i]=find(a[i]);
	for(int i=1;i<=n;i++){
    	if(vis[i])continue;
    	int now=i;
		int Min2=(int)1<<60,cnt=0,sum=0;
		while(!vis[now]){//遍历环
			cnt++;sum+=a[now];vis[now]=1;
    		Min2=min(Min2,a[now]);
    		now=nxt[now];
		}
    	int now1=(cnt-1)*Min2+sum-Min2;
    	int now2=cnt*Min1+sum+Min2+Min1;
    	ans+=min(now1,now2);//计算代价
    }
	printf("%lld\n",ans);
	return 0;
}

都看到这里了，能不能给个赞呢？

有不懂随时@我。

蒟蒻第一篇题解写得不好请见谅。