自动搬运

查看原文

来自洛谷，原作者为

	Antarctica_Oabaijnaw 人类的勇气，可以跨越时间，跨越每一个历史，当下，和未来||鼓足干劲、力争上游、多快好省地建设洛谷的总路线||末日时在颓什么？有没有空？可以来拯救吗？||オーバイジュナウ||OUR MIGHTY FALLEN,BE GOTTEN POWER

搬运于2025-08-24 22:18:07，当前版本为作者最后更新于2025-08-13 21:22:32，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

神仙题，我说的。

各位大佬都讲了这玩意要把问题转化成欧拉回路，这里主要讲的是一些细节问题，有些口水话，还望各位见谅。

首先发现 $\leq s_i$ $\text{km/h}$ 的条件很棘手，但是加速没有任何代价，于是强制规定必须等于 $s_i$ $\text{km/h}$。

随后肯定需要将已知条件建模，每个车站从 $s_i$ 向 $t_i$ 连边，同时建一个虚点 inf，让 inf 向 1 连边，现在 $s_i$ 和 $t_i$ 中的最大值向 inf 连边，然后补一些边使整个图形成欧拉回路，问补上的那些边的边权之和最小是多少。

这就是正解思路了（前人之述备矣），但是初看肯定会一头雾水，所以画图理解一下，这题不画图就是石：

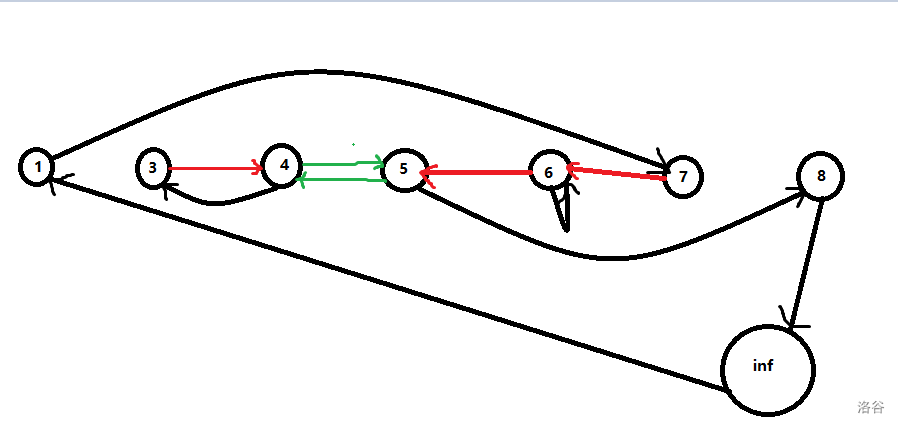
样例，其中黑色的边是我们最初建的，其他颜色的边是补上的。

解释一下：

• 以 $1$ $\text{km/h}$ 进入 $0$ 号路段，以 $7$ $\text{km/h}$ 的速度离开该路段（点 1 到点 7）
• 减速至 $6$ $\text{km/h}$，花费代价为 1（点 7 到点 6）
• 以 $6$ $\text{km/h}$ 进入 $3$ 号路段并以相同的速度离开该路段（点 6 到点 6 自环）
• 减速至 $4$ $\text{km/h}$，花费代价为 2（点 6 到点 4）
• 以 $4$ $\text{km/h}$ 进入 $1$ 号路段，以 $3$ $\text{km/h}$ 的速度离开该路段（点 4 到点 3）
• 提速至 $5$ $\text{km/h}$，不花费代价（点 3 到点 6）
• 以 $5$ $\text{km/h}$ 进入 $2$ 号路段，以 $8$ $\text{km/h}$ 的速度离开该路段（点 5 到点 8）
• 以 $8$ $\text{km/h}$ 进入第一条虚路段，以 $\text{inf\ km/h}$ 的速度离开该路段（点 8 到点 inf）
• 以 $\text{inf\ km/h}$ 进入第二条虚路段，以 $1$ $\text{km/h}$ 的速度离开该路段（点 inf 到点 1）
• 自此回到点 1，所有的边都只经过一次，形成欧拉回路

现在应该懂了吧。

然后，我们反过来研究一下如果图是欧拉回路会有什么性质。我们观察两个相邻的点，惊人的发现：对于所有横跨这两个节点（对于“横跨”，举例解释一下，比如 $0$ 号路段从点 1 到点 7，就横跨了 点 1 和 点 3 等）的边，加速的和减速的边数相等！

证明也是显然的，因为欧拉回路是每一条边都要经过的，这一次是通过加速边，下一次一定是过减速边，而由于是回路，所以去和回一一对应，次数一定相等。

于是可以差分处理每一对相邻的点覆盖的初始黑边数量，然后对每一对相邻的点补上加速边或减速边，就补成了上图去掉绿边的样子。由于边数差可能大于 1，所以有时得补多条边，差分的时候乘上边数就行了。

这时我们尴尬地发现，这个补过的图可能不连通！为了将图连通，我们用并查集处理连通块，对于每一对不在同一个连通块内的相邻的点，我们都可以补上一对双向边，就是图中的绿边。而不一定所有可以补的都要补上，所以用最小生成树（MST）处理一下。

然后因为 $s_i$ 和 $t_i$ 的值域很大要离散化一下，差不多就口胡完了。

代码就不贴注释了，上面已经讲得很明白了。

#include<bits/stdc++.h>
#define int  long long
using namespace std;
int n,m,s[200005],t[200005],d[400005]; 
int fa[400005];
int find(int x){
	if(x==fa[x])return x;
	return fa[x]=find(fa[x]); 
}
void join(int x,int y){
	int fx=find(x),fy=find(y);
	if(fx==fy)return;
	fa[fx]=fy;
}
struct edge{
	int u,v,w;
	bool operator<(const edge &o)const{
		if(w==o.w&&u==o.u)return v<o.v;
		if(w==o.w)return u<o.u;
		return w<o.w;
	}
};
signed main(){
	cin>>n>>m;
	vector<int>l;
	for(int i=1;i<=n;i++)cin>>s[i]>>t[i],l.push_back(s[i]),l.push_back(t[i]);
	n++;
	s[n]=INT_MAX,t[n]=1;
	l.push_back(s[n]),l.push_back(t[n]);
	n++;
	s[n]=INT_MAX-1,t[n]=INT_MAX;
	l.push_back(s[n]),l.push_back(t[n]);
	sort(l.begin(),l.end());
	l.erase(unique(l.begin(),l.end()),l.end());
	for(int i=0;i<l.size();i++)fa[i]=i;
	for(int i=1;i<=n;i++){
		s[i]=lower_bound(l.begin(),l.end(),s[i])-l.begin();
		t[i]=lower_bound(l.begin(),l.end(),t[i])-l.begin();
		d[s[i]]++;
		d[t[i]]--;
		join(s[i],t[i]);
	}
	int sum=0;
	for(int i=1;i<l.size();i++)d[i]+=d[i-1];
	for(int i=0;i<l.size()-1;i++){
		if(d[i]!=0)join(i,i+1);
		if(d[i]>0)sum+=(l[i+1]-l[i])*d[i];
	}
	vector<edge>edges;
	for(int i=1;i<l.size();i++){
		int fi=find(i-1),fii=find(i);
		if(fi!=fii)edges.push_back({i-1,i,l[i]-l[i-1]});
	}
	sort(edges.begin(),edges.end());
	for(auto x:edges){
		int fu=find(x.u),fv=find(x.v);
		if(fu==fv)continue;
		fa[fu]=fv;
		sum+=x.w;
	}
	cout<<sum<<endl;
}//Vive la Furina!