自动搬运

查看原文

来自洛谷，原作者为

	泥土笨笨 《算法竞赛实战笔记》作者

搬运于2025-08-24 22:17:55，当前版本为作者最后更新于2020-03-01 23:21:51，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

数据量$10^5$，如果依次取枚举三角形的三个顶点，复杂度$O(n^3)$，必然超时。题目中说只关心一条边和x轴重合，另一条边和y轴重合的三角形，那么这两条边组成了一个直角，我们先尝试枚举这个直角，看看以一个点作为直角顶点，能组成的所有三角形面积能否快速求出。

考虑如下图的样子

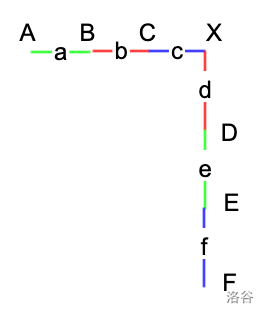
X点是我们所求的点，在X的左边还有A，B，C三个点，他们纵坐标相等。在X的下方还有F，E，D三个点，他们横坐标相等。那么此时以X为直角顶点，能组成多少个三角形，他们的面积的二倍的和是多少呢。我们设两点之间的线段长度已经用小写字符标在图上，可以算出，现在的总面积是：

$$(a+b+c)*d+(b+c)*d+c*d+(a+b+c)*(d+e)+(b+c)*(d+e)+c*(d+e)+(a+b+c)*(d+e+f)+(b+c)*(d+e+f)+c*(d+e+f) $$$$=(a+2*b+3*c)*(f+2*e+3*d)$$

这个点的值，只和与自己横坐标相同的点，和与自己纵坐标相同的点有关。而且有点类似于前缀和，可以开一个数组，去记录每个横纵坐标各自积累的和是多少。当又来了一个新点，则把这个点对应的横坐标位置的和，加上4倍与上一个点之间的距离。纵坐标位置的和同理处理，所以我们发现还需要记录每行每列出现了几个数字了。再来一个新点，就加5倍距离，以此类推。

那么，我们按照x坐标从小到大，y坐标从小到大的顺序，依次去枚举每个点i，去做一下上述处理，然后计算结果出来。但是这个计算方式只对目前我们这种方向的三角形有效，事实上三角形的直角有四个方向，分别是冲着一二三四四个象限的方向。现在我们处理的，是直角在第三象限的情况。不过并不难处理，只要改一下点的排序方式，把同样的事情做4遍就行了。

代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
typedef long long ll;
const ll MAXN = 100005;
const ll MOD = 1e9 + 7;
const ll DIF = 10005;

struct Point {
    ll x, y;
} points[MAXN];

ll n, sumX[2 * DIF], sumY[2 * DIF], cntX[2 * DIF], cntY[2 * DIF];
ll lastX[2 * DIF], lastY[2 * DIF], ans;

bool cmp1(const Point &a, const Point &b) {
    if (a.x != b.x) return a.x < b.x;
    return a.y < b.y;
}

bool cmp2(const Point &a, const Point &b) {
    if (a.x != b.x) return a.x < b.x;
    return a.y > b.y;
}

bool cmp3(const Point &a, const Point &b) {
    if (a.x != b.x) return a.x > b.x;
    return a.y < b.y;
}

bool cmp4(const Point &a, const Point &b) {
    if (a.x != b.x) return a.x > b.x;
    return a.y > b.y;
}

void work() {
    memset(sumX, 0, sizeof(sumX));//sumX数组，存每个x坐标对应的和目前是多少
    memset(sumY, 0, sizeof(sumY));//存每个y坐标对应的和
    memset(cntX, 0, sizeof(cntX));//存每个x坐标出现过多少个数字了
    memset(cntY, 0, sizeof(cntY));
    for (ll i = 0; i < n; ++i) {//依次枚举每个点
        //用x和y记录一下当前点的x和y坐标，下面写起来轻松一点
        ll x = points[i].x, y = points[i].y;
        //当前x方向上的和，加上新点到上次的点的距离，乘以目前点的个数
        sumX[x] = (sumX[x] + abs(y - lastX[x]) * cntX[x]) % MOD;
        cntX[x]++;//多了一个点了
        lastX[x] = y;//记一下当前这个点的y值，下次跟这个来做差
        sumY[y] = (sumY[y] + abs(x - lastY[y]) * cntY[y]) % MOD;
        cntY[y]++;
        lastY[y] = x;
        ans = (ans + sumX[x] * sumY[y]) % MOD;//计算结果
    }
}

int main() {
    freopen("triangles.in","r",stdin);
    freopen("triangles.out","w",stdout);
    scanf("%lld", &n);
    for (int i = 0; i < n; ++i) {
        scanf("%lld%lld", &points[i].x, &points[i].y);
        points[i].x += DIF;
        points[i].y += DIF;
    }
    //先延x从小到大，y从小到大的顺序排序，计算结果
    sort(points, points + n, cmp1);
    work();
    //其他方向依次处理
    sort(points, points + n, cmp2);
    work();
    sort(points, points + n, cmp3);
    work();
    sort(points, points + n, cmp4);
    work();
    printf("%lld\n", ans);
    return 0;
}