自动搬运

查看原文

来自洛谷，原作者为

	EternalAlexander 魔力的碎片都不再拥有的少年

搬运于2025-08-24 22:17:46，当前版本为作者最后更新于2020-02-27 13:58:56，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

发现毒瘤们想强迫我们写平衡树，因此，我们考虑怎么不写平衡树。

发现有个东西叫做 01trie。这玩意可以当平衡树用，不会的可以看这里。

然而并不能通过这个题，因为可恶的毒瘤们卡了空间，而 01trie 的空间复杂度是 $O(n\log w)$，其中 $w$ 是值域。

然而，这棵树的叶节点数量是 $O(n)$ 的，因此，假如我们能通过某种办法把它的所有单链压缩起来，这棵树上的节点数就会变成 $O(n)$。因为所有 $n$ 个叶节点的虚树大小只有 $O(n)$。

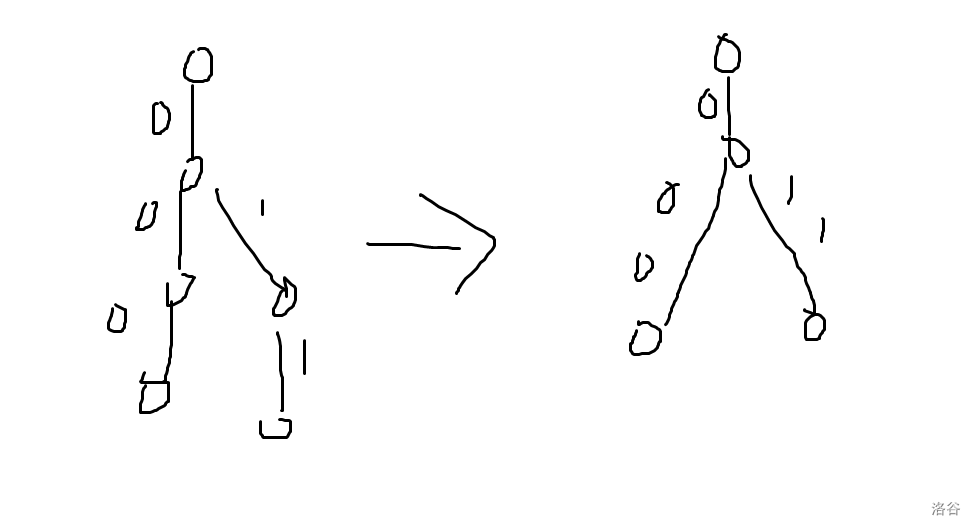
实现起来，大概就是和普通 01trie 一样地从根节点向下匹配，然后假如遇到失配，就分裂当前节点。

如果你学习过后缀树，你会发现这个东西的实现方式和后缀树非常类似。

这样，空间复杂度可以达到 $O(n)$，我们就能愉快地不写平衡树而通过本题了。

#include <bits/stdc++.h>
const int maxn = 2000005,lim=30;
const int base=1e7;
int g(int x,int i){return (x>>i)&1;}
int reverse(int x){
	int ans=0;
	for(int i=0;i<lim;++i)ans+=g(x,i)<<(lim-i-1);
	return ans;
}
struct compressed_trie {
	int ch[maxn*2][2],d[maxn*2],v[maxn*2],pt[maxn*2],size[maxn*2],tl=1;
	int newnode(int p,int dep){
		pt[++tl]=p;d[tl]=dep;return tl;
	}void insert(int x,int det){
		int v1=x;x=reverse(x);
		int rt=1,rem=0,last=0;
		for(int i=0;i<lim;++i){
			rem++;int c1=g(x,i);
			while(i>d[rt]){
				if(!ch[rt][c1]){
					ch[rt][c1]=newnode(x>>i,lim);
					v[tl]=v1;
					size[ch[rt][c1]]=det;
					return;
				}last=rt;rem=i-d[rt];rt=ch[rt][c1];
				size[last]+=det;
			}int c2=g(pt[rt],rem-1);
			if(c1!=c2){
				int u=newnode(pt[rt],i-1);size[u]=size[rt]+det;
				ch[u][c2]=rt;ch[u][c1]=newnode(x>>i,lim);
				ch[last][g(pt[rt],0)]=u;
				pt[rt]>>=(rem-1);
				last=u;rt=ch[u][c1];rem=1;size[rt]+=det;v[rt]=v1;
				return;
			}
		}size[rt]+=det;
	}int rank(int x){
		insert(x,0);
		x=reverse(x);int rt=1,ans=0;	
		for(int i=0;i<lim;++i){
			int c1=g(x,i);
			while(i>d[rt]){
				if(c1==1)ans+=size[ch[rt][0]];
				rt=ch[rt][c1];
			}
		}return ans;
	}int kth(int x,int rt=1){
		if(rt==1)insert(x,0);
		if(!ch[rt][0]&&!ch[rt][1])return v[rt];
		if(x<=size[ch[rt][0]])return kth(x,ch[rt][0]);
		else return kth(x-size[ch[rt][0]],ch[rt][1]);
	}	
}T; 
int opt,t,n,q,sum,lastans;
int main() {
	T.d[1]=-1;
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;++i){scanf("%d",&t);T.insert(t,1);}
	while (q--) {
		scanf("%d %d",&opt,&t);t^=lastans;
		if (opt==1) T.insert(t, 1);
		if (opt==2) T.insert(t, -1);
		if(opt<=2)continue;
		if (opt==3)lastans=T.rank(t)+1;
		if (opt==4)lastans=T.kth(t);
		if (opt==5)lastans=T.kth(T.rank(t));
		if (opt==6)lastans=T.kth(T.rank(t+1)+1);
		sum^=lastans;
	}printf("%d",sum);
	return 0;
}