自动搬运

查看原文

来自洛谷，原作者为

	wucstdio 这个家伙不懒，但还是什么都没留下

搬运于2025-08-24 22:17:33，当前版本为作者最后更新于2020-02-18 16:33:06，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

大概是我贡献的第二道模板？

$\text{Lyndon}$ 分解详解

我们定义一个串是 $\text{Lyndon}$ 串，当且仅当这个串的最小后缀就是这个串本身。

该命题等价于这个串是它的所有循环表示中字典序最小的。

---

引理 1：如果 $u$ 和 $v$ 都是 $\text{Lyndon}$ 串并且 $u<v$，则 $uv$ 也是 $\text{Lyndon}$ 串。

证明：

1、若 $\operatorname{len}(u)\ge\operatorname{len}(v)$

这时，$u$ 和 $v$ 这两个串在 $\operatorname{len}(v)$ 之前就出现了不同的字符，所以有 $v>uv$，又因为 $v$ 是 $\text{Lyndon}$ 串，所以 $v$ 的所有后缀都大于 $v$，所以 $uv$ 的所有后缀都大于 $uv$，故 $uv$ 是 $\text{Lyndon}$ 串。

2、若 $\operatorname{len}(u)<\operatorname{len}(v)$

若 $u$ 不是 $v$ 的前缀，那么有 $v>uv$，得证。

若 $u$ 是 $v$ 的前缀，那么如果 $v<uv$，则必有 $v[\operatorname{len}(u)+1:]<v$（也就是各自去掉了前 $|u|$ 个字符），矛盾。

---

我们定义一个串 $S$ 的 $\text{Lyndon}$ 分解为一个字符串序列 $A_1,A_2,\dots,A_m$，满足：

• $\forall i \in [1,m]$，满足 $A_i$ 是 $\text{Lyndon}$ 串。
• $\forall i \in [1,m-1]$，满足 $A_i\ge A_{i+1}$。

可以证明这种划分存在且唯一。

存在性证明

初始令 $m=|S|$ 并且 $A_i=S[i]$，然后每次不断找到 $A_i<A_{i+1}$ 并且合并为一个串。最后一定能使得所有的 $A_i\ge A_{i+1}$。

唯一性证明

假设对于字符串 $S$ 存在两个 $\text{Lyndon}$ 分解：

$$S=A_1A_2\cdots A_iA_{i+1}A_{i+2}\cdots A_{m_1}$$ $$S=A_1A_2\cdots A_iA^\prime_{i+1}A^\prime_{i+2}\cdots A^\prime_{m_1} $$

不妨设 $\operatorname{len}(A_{i+1})>\operatorname{len}(A^\prime_{i+1})$。

观察 $A_{i+1}$ 在第二种分解中的对应情况。假设 $A_{i+1}=A^\prime_{i+1}A^\prime_{i+2}\cdots A^\prime_{k}A^\prime_{k+1}[:l]$。

那么由 $\text{Lyndon}$ 串的性质可知：

$$A_{i+1}<A^\prime_{k+1}[:l]\le A^\prime_{k+1}\le A^\prime_{i+1}<A_{i+1} $$

矛盾。

---

引理2：若字符串 $v$ 和字符 $c$ 满足 $vc$ 是某个 $\text{Lyndon}$ 串的前缀，则对于字符 $d>c$ 有 $vd$ 是 $\text{Lyndon}$ 串。

证明：

设该 $\text{Lyndon}$ 串为 $v+c+t$。

则 $\forall i \in [2,|v|],v[i:]+c+t>v+c+t$，也就是说 $v[i:]+c\ge v$。

所以 $v[i:]+d>v[i:]+c\ge v$。

同时因为 $c>v[1]$，我们有 $d>c>v[1]$。

故 $v+d$ 是一个 $\text{Lyndon}$ 串。

---

$\text{Duval}$ 算法

这个算法可以在 $O(n)$ 时间复杂度，$O(1)$ 空间复杂度内求出一个串的 $\text{Lyndon}$ 分解。

该算法中我们仅需维护三个变量 $i,j,k$。

维持一个循环不变式：

• $s[:i-1]=s_1s_2\cdots s_g$ 是固定下来的分解，也就是 $\forall l\in[1,g],s_l$ 是 $\text{Lyndon}$ 串且 $s_l>s_{l+1}$。
• $s[i,k-1]=t^h+v(h>1)$ 是没有固定的分解，满足 $t$ 是 $\text{Lyndon}$ 串，且 $v$ 是 $t$ 的可为空的不等于 $t$ 的前缀，且有 $s_g>s[i,k-1]$

如下图：

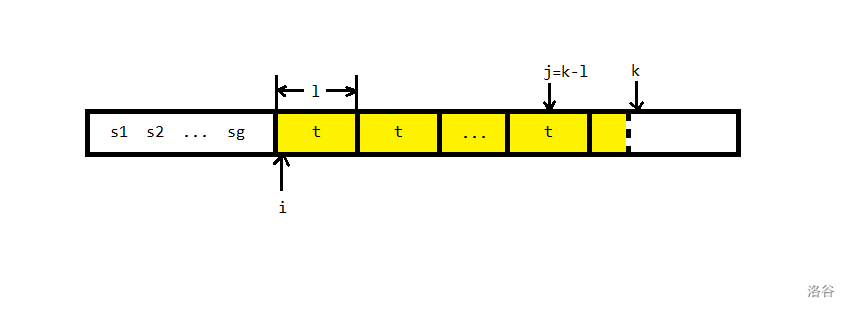
当前读入的字符是 $s[k]$，令 $j=k-|t|$。

分三种情况讨论：

• 当 $s[k]=s[j]$ 时，直接 $k\leftarrow k+1,j\leftarrow j+1$，周期 $k-j$ 继续保持
• 当 $s[k]>s[j]$ 时，由引理 2 可知 $v+s[k]$ 是 $\text{Lyndon}$ 串，由于 $\text{Lyndon}$ 分解需要满足 $s_i\ge s_{i+1}$，所以不断向前合并，最终整个 $t^h+v+s[k]$ 形成了一个新的 $\text{Lyndon}$ 串。
• 当 $s[k]<s[j]$ 时，$t^h$ 的分解被固定下来，算法从 $v$ 的开头处重新开始。

复杂度分析：$i$ 只会单调往右移动，同时 $k$ 每次移动的距离不会超过 $i$ 移动的距离，所以时间复杂度是 $O(n)$ 的。

代码如下：

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
char s[5000005];
int n,ans;
int main()
{
	scanf("%s",s+1);
	n=(int)strlen(s+1);
	for(int i=1;i<=n;)
	{
		int j=i,k=i+1;//初始化
		while(k<=n&&s[j]<=s[k])
		{
			if(s[j]<s[k])j=i;//合并为一整个
			else j++;//保持循环不变式
			k++;
		}
		while(i<=j)//从v的开头重新开始
		{
			ans^=i+k-j-1;
			i+=k-j;
		}
	}
	printf("%d\n",ans);
	return 0;
}