自动搬运

查看原文

来自洛谷，原作者为

	海洋守卫者 不积跬步，无以至千里；不积小流，无以成江海。

搬运于2025-08-24 22:17:13，当前版本为作者最后更新于2025-04-11 17:45:32，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P6081 - Barn Expansion 牛棚扩张

【双倍经验】

解题思路

一种基于“贪心-区间问题”的优雅暴力解题方法。

根据题意，如果两个牛棚的边有相交的部分，那么这两个牛棚都不可扩张。

首先观察样例，我们可以得出下图：

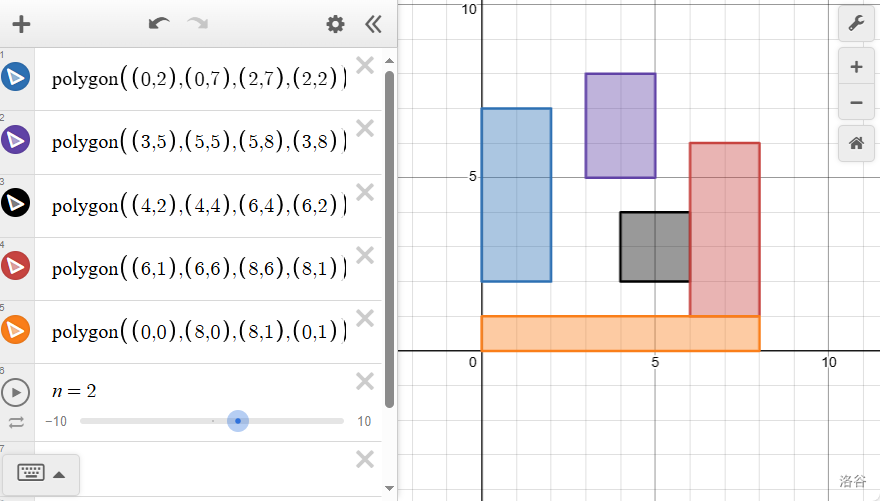
此时结合题面，有人就会得出结论：两两矩形之间不可能相交。

说的太对了！但这条信息对于本篇题解没有任何意义。

请再次用我们大大的眼睛去好好盯一盯这张图片，将眼光从最左边，缓缓地移到最右边——你就会发现，如果两个矩形的边有重合的部分，那两个矩形在横坐标轴上的投影必然相交——假设共用一个端点也算相交的话。（不用我解释投影是什么吧）

这也太明显了！小学二年级的同学也可以看出来好吧。这真的对解题有帮助吗？

你想想，如果这样的话，那我是不是可以利用这一条性质，写一份优化过的 $O(n^2)$ 的暴力……嗯？

按照左边界为第一关键字，下边界为第二关键字（用于加速），对所有矩形进行排序。然后，从左往右，选定一个矩形，再从左往右扫描与他横坐标相交的矩形，判断纵坐标上是否相交，是的话就将两者全部标记（说白了就是暴力）。

虽然时间复杂度为 $O(n^2)$，但实际可以跑得飞快。

关键代码如下：

sort(p+1,p+1+n,cmp);
for(int i=1;i<=n;i++)
{
	int l=p[i].a,r=p[i].c,u=p[i].d,d=p[i].b;  //左、右、上、下
	for(int j=i+1;j<=n&&p[j].a<=r;j++)
	{
		if(p[j].d>=d&&p[j].b<=u)could[i]=could[j]=false;
	}
}

实现细节

本题不要多测清空，除此之外没有任何细节。

完整代码

#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
struct Square{
	int a,b,c,d;
}p[50005];
inline bool cmp(Square A,Square B)
{
	return A.a<B.a;
}
bool could[50005];
int n,ans;
int main()
{ 
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d %d %d %d",&p[i].a,&p[i].b,&p[i].c,&p[i].d);
		if(p[i].a>p[i].c)swap(p[i].a,p[i].c);
		if(p[i].b>p[i].d)swap(p[i].b,p[i].d);
		could[i]=true;
	}
	sort(p+1,p+1+n,cmp);
	for(int i=1;i<=n;i++)
	{
		int l=p[i].a,r=p[i].c,u=p[i].d,d=p[i].b;  //左、右、上、下
		for(int j=i+1;j<=n&&p[j].a<=r;j++)if(p[j].d>=d&&p[j].b<=u)could[i]=could[j]=false;
	}
	for(int i=1;i<=n;i++)if(could[i])ans++;
	printf("%d",ans);
	return 0;
}