自动搬运

查看原文

来自洛谷，原作者为

	Zjl37 I could call myself a programmer no matter how little I know (0275.)

搬运于2025-08-24 22:17:12，当前版本为作者最后更新于2020-03-01 10:41:54，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

本篇题解的目的

Click here

树形动规

注意到一头奶牛最多只有一个母亲，且不存在环，因此可以用树来储存；母女关系又具有明显的方向性，可以单向存边。所有奶牛及其关系构成一片森林。
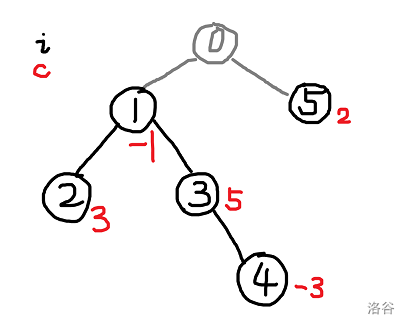
如果一头奶牛的母亲不是候选奶牛，不妨将其母亲编号为 0，这样一片森林就变成了一棵以0为根的树，方便我们读入和操作。

这是一张样例的图：

设计状态

设计一个三维数组 f：
$f(i,j,0)$ 表示牛 i 不参赛，以 i 为根的家庭树下有 j 对血缘关系时最大的产奶量。
$f(i,j,1)$ 表示牛 i 参赛，以 i 为根的家庭树中有 j 对血缘关系时最大的产奶量。

另外，维护一个一维数组 cnt：$cnt(i)$ 表示以 i 为根的家庭树中的边数。这也表示树中最多可能的血缘关系数，可以用来确定枚举边界。

最后的答案是一个最大的数 m，满足 $f(0,m,0)\geq x$。因为牛 0 不是候选奶牛，它不能参赛，所以第三维只能是 0.

状态转移与初始值

考虑一头奶牛 x：
很显然，初始时 $f(x,0,0) = 0,\; f(x,0,1) = c(x)$，其中 $c(i)$ 表示牛 i 能为全队贡献的牛奶体积。其他的值，到目前为止都是无穷小。

接下来，将 x 的女儿的信息合并到 x 中。考虑母亲 x 的女儿 y，假定在 y 之前枚举的所有女儿的信息都已经合并到了 x 中。在 x 中选 j 对关系，在 y 中选 k 对关系，那么 j, k 的取值范围：$0\leq j\leq cnt(x),\; 0\leq k\leq cnt(y)$
（ 啊，如果你觉得这段话读起来怪怪的，换成父节点、子节点之类不影响理解 ）

• 如果 x 参赛，y 也参赛，那么 x 与 y 形成一对新的血缘关系，一共有 j + k + 1 对关系。
  $ f(x,j+k+1,1)=\max\lbrace f(x,j+k+1,1),f(x,j,1)+f(y,k,1)\rbrace $

其他情况下不形成新关系，也就只有 j + k 对关系。

• 如果 x 参赛，y 不参赛：
  $ f(x,j+k,1)=\max\lbrace f(x,j+k,1),f(x,j,1)+f(y,k,0)\rbrace $
• 如果 x 不参赛，那么取 y 参赛和不参赛中较大的产奶量：
  $ f(x,j+k,0)=\max\lbrace f(x,j+k,0),f(x,j,0)+\max\lbrace f(y,k,0),f(y,k,1) \rbrace \rbrace $

代码（AC 100）

#include <bits/stdc++.h>
using namespace std;

int n,x,c[501],mo,es,hd[501],f[501][501][2],cnt[501];
// mo: mother, es: 邻接表中已经存的边数, hd[i]: 邻接表中从i出发的最后一条边。其他变量的含义同题面和题解。
pair<int,int> e[501]; // <daughter,next>
// 使用邻接表存边。
// STL之pair真好用，使用时建议将first、second代表的含义记在旁边，避免忘记。

void add(int x, int y) {
	// add函数用于向邻接表中添加一条从x到y的边，表示x是y的母亲。
	e[++es]=make_pair(y,hd[x]);
	hd[x]=es;
}

void dfs(int x) {
	// dfs函数进行树形动规，x为当前的牛
	f[x][0][0]=0;
	f[x][0][1]=c[x];
	// 初始值
	for(int i=hd[x]; i; i=e[i].second) {
		int y=e[i].first;
		// 因为是有向边，不必判断y是否等于母亲
		dfs(y);
		// 先搜女儿
		for(int j=cnt[x]; j>=0; j--) {
			for(int k=cnt[y]; k>=0; k--) {
				if(f[x][j][0]+max(f[y][k][0],f[y][k][1])>f[x][j+k][0])
					f[x][j+k][0]=f[x][j][0]+max(f[y][k][0],f[y][k][1]);
				// x不参赛
				if(f[x][j][1]+f[y][k][1]>f[x][j+k+1][1])
					f[x][j+k+1][1]=f[x][j][1]+f[y][k][1];
				// x参赛，y参赛
				if(f[x][j][1]+f[y][k][0]>f[x][j+k][1])
					f[x][j+k][1]=f[x][j][1]+f[y][k][0];
				// x参赛，y不参赛
			}
		}
		cnt[x]+=cnt[y]+1;
		// 维护边数。x的边数是它所有女儿的边数，加上它女儿的数量。
	}
}

int main() {
//	freopen("XPtselect.in","r",stdin);
//	freopen("XPtselect.out","w",stdout);
	scanf("%d%d",&n,&x);
	for(int i=1; i<=n; i++) {
		scanf("%d%d",&c[i],&mo);
		add(mo,i);
		// 存有向边
	}
	memset(f,0xc0,sizeof f);
	// 将f数组中的所有值初始化为(int)0xc0c0c0c0=-1061109568，可看做无穷小。
	dfs(0);
	while(n>=0&&f[0][n][0]<x)
		n--;
	// 从大到小查找答案。当然也可以写二分查找，不过意义不大。
	printf("%d\n",n);
	return 0;
}